Lesson 7: Inferences Regarding Multivariate Population Mean
Lesson 7: Inferences Regarding Multivariate Population MeanOverview
This lesson deals with inference for a multivariate population mean. Similar to a univariate population, inference problems may arise in three different scenarios:
- Case I: Inference problems regarding a single multivariate population
- Case II: Inference problems regarding two means from a paired population
- Case III: Inference problems regarding two means from two independent populations
All three cases are dealt with briefly in this lesson. All three cases make use of Hotelling's T-square statistic.
This lesson plan is divided into two parts: Basic and Advanced. In the basic section, we will introduce standard methods for statistical inference on mean vectors. The advanced section will discuss topics such as adjusting for multiple comparisons, profile analysis, etc.
Objectives
- Carry out Hotelling's T-square test for testing a population mean vector that meets specifications;
- Carry out Hotelling's T-square test for comparing two independent/paired population mean vectors;
- Compute and interpret simultaneous and Bonferroni confidence intervals;
7.1 - Basic
7.1 - BasicIn this section, we will introduce the standard statistical methods for making inferences on the multivariate population mean.
7.1.1 - An Application of One-Sample Hotelling’s T-Square
7.1.1 - An Application of One-Sample Hotelling’s T-SquareWomen’s Health Survey: One-Sample Hotelling's T-Square
In 1985, the USDA commissioned a study of women’s nutrition. Nutrient intake was measured for a random sample of 737 women aged 25-50 years. Five nutritional components were measured: calcium, iron, protein, vitamin A, and vitamin C. In previous analyses of these data, the sample mean vector was calculated. The table below shows the recommended daily intake and the sample means for all the variables:
| Variable | Recommended Intake \((\mu_{o})\) | Mean |
|---|---|---|
| Calcium | 1000 mg | 624.0 mg |
| Iron | 15mg | 11.1 mg |
| Protein | 60g | 65.8 g |
| Vitamin A | 800 μg | 839.6 μg |
| Vitamin C | 75 mg | 78.9 mg |
One of the questions of interest is whether women meet the federal nutritional intake guidelines. If they fail to meet the guidelines, then we might ask for which nutrients the women fail to meet the guidelines.
The hypothesis of interest is that women meet nutritional standards for all nutritional components. This null hypothesis would be rejected if women fail to meet nutritional standards on any one or more of these nutritional variables. In mathematical notation, the null hypothesis is the population mean vector \(μ\) equals the hypothesized mean vector \(\mu_{o}\) as shown below:
\(H_{o}\colon \mu = \mu_{o}\)
Let us first compare the univariate case with the analogous multivariate case in the following tables.
Focus of Analysis
Measuring only a single nutritional component (e.g. Calcium).
Data: scalar quantities \(X _ { 1 } , X _ { 2 } , \ldots , X _ { n }\)
Measuring multiple (say p) nutritional components (e.g. Calcium, Iron, etc).
Data: p × 1 random vectors
\(\mathbf{X} _ { 1 } , \mathbf{X} _ { 2 } , \ldots , \mathbf{X} _ { n }\)
Assumptions Made In Each Case
Distribution
The data all have a common mean \(\mu\) mathematically, \(E \left( X _ { i } \right) = \mu; i = 1,2, \dots, n\) This implies that there is a single population of subjects and no sub-populations with different means.
The data have a common mean vector \(\boldsymbol{\mu}\); i.e., \(E \left( \boldsymbol { X } _ { i } \right) =\boldsymbol{\mu}; i = 1,2, . , n \) This also implies that there are no sub-populations with different mean vectors.
Homoskedasticity
The data have common variance \(\sigma^{2}\) ; mathematically, \(\operatorname { var } \left( X _ { i } \right) = \sigma ^ { 2 } ; i = 1,2 , . , n\)
The data for all subjects have common variance-covariance matrix \(Σ\) ; i.e., \(\operatorname { var } \left( \boldsymbol{X} _ { i } \right) = \Sigma ; i = 1,2 , \dots , n\)
Independence
The subjects are independently sampled.
The subjects are independently sampled.
Normality
The subjects are sampled from a normal distribution
The subjects are sampled from a multivariate normal distribution.
Hypothesis Testing in Each Case
Consider hypothesis testing:
\(H _ { 0 } \colon \mu = \mu _ { 0 }\)
against alternative
\(H _ { \mathrm { a } } \colon \mu \neq \mu _ { 0 }\)
Consider hypothesis testing:
\(H _ { 0 } \colon \boldsymbol{\mu} = \boldsymbol{\mu _ { 0 }}\) against \(H _ { \mathrm { a } } \colon \boldsymbol{\mu} \neq \boldsymbol{\mu _ { 0 }}\)
Here our null hypothesis is that mean vector \(\boldsymbol{\mu}\) is equal to some specified vector \(\boldsymbol{\mu_{0}}\). The alternative is that these two vectors are not equal.
We can also write this expression as shown below:
\(H_0\colon \left(\begin{array}{c}\mu_1\\\mu_2\\\vdots \\ \mu_p\end{array}\right) = \left(\begin{array}{c}\mu^0_1\\\mu^0_2\\\vdots \\ \mu^0_p\end{array}\right)\)
The alternative, again is that these two vectors are not equal.
\(H_a\colon \left(\begin{array}{c}\mu_1\\\mu_2\\\vdots \\ \mu_p\end{array}\right) \ne \left(\begin{array}{c}\mu^0_1\\\mu^0_2\\\vdots \\ \mu^0_p\end{array}\right)\)
Another way of writing this null hypothesis is shown below:
\(H_0\colon \mu_1 = \mu^0_1\) and \(\mu_2 = \mu^0_2\) and \(\dots\) and \(\mu_p = \mu^0_p\)
The alternative is that μj is not equal to \(\mu^0_j\) for at least one j.
\(H_a\colon \mu_j \ne \mu^0_j \) for at least one \(j \in \{1,2, \dots, p\}\)
Univariate Statistics: \(t\)-test
In your introductory statistics course, you learned to test this null hypothesis with a t-statistic as shown in the expression below:
\(t = \dfrac{\bar{x}-\mu_0}{\sqrt{s^2/n}} \sim t_{n-1}\)
Under \(H _ { 0 } \) this t-statistic has a t distribution with n-1 degrees of freedom. We reject \(H _ { 0 } \) at level \(α\) if the absolute value of the test statistic t is greater than the critical value from the t-table, evaluated at \(α/2\) as shown below:
\(|t| > t_{n-1, \alpha/2}\)
7.1.2 - A Naive Approach
7.1.2 - A Naive ApproachFollowing the univariate method, a naive approach for testing a multivariate hypothesis is to compute the t-test statistics for each individual variable; i.e.,
\(t_j = \dfrac{\bar{x}_j-\mu^0_j}{\sqrt{s^2_j/n}}\)
Thus we could define \(t_{j}\), which would be the t-statistic for the \(j^{th}\) variable as shown above. We may then reject \(H_0\colon \boldsymbol{\mu} = \boldsymbol{\mu_0}\) if \(|t_j| > t_{n-1, \alpha/2}\) for at least one variable \(j \in \{1,2,\dots, p\}\) .
Problem with Naive Approach
The basic problem with this naive approach is that it does not control the family-wise error rate. By definition, the family-wise error rate is the probability of rejecting at least one of the null hypotheses \(H^{(j)}_0\colon \mu_j = \mu^0_j\) when all of the \(H_{0}\)’s are true.
To understand the family-wise error rate suppose that the experimental variance-covariance matrix is diagonal. This implies zero covariances between the variables. If the data are multivariate and normally distributed then this would mean that all of the variables are independently distributed. In this case, the family-wide error rate is
\(1-(1-\alpha)^p > \alpha\)
where p is the dimension of the multivariate data and \(α\) is the level of significance. By definition, the family-wide error rate is equal to the probability that we reject \(H _ { 0 } ^ { ( j ) }\) for at least one j, given that \(H _ { 0 } ^ { ( j ) }\) is true for all j. Unless p is equal to one, the error will be strictly greater than \(α\).
Consequence
The naive approach yields a liberal test. That is, we will tend to reject the null hypothesis more often than we should.
Bonferroni Correction
Under the Bonferroni Correction, we would reject the null hypothesis that mean vector \(\boldsymbol{\mu}\) is equal to our hypothesized mean vector \(\boldsymbol{\mu_{0}}\) at level \(\alpha\) if, for at least one variable j, the absolute value of \(t_{j}\) is greater than the critical value from the t-table with n-1 degrees of freedom evaluated at \(\alpha /(2p)\) for at least one variable j between 1 and p.
Note! For independent data, this yields a family-wide error rate of approximately \(\alpha\). For example, the family-wide error rate is shown in the table below for different values of p. You can see that these are all close to the desired level of \(\alpha = 0.05\).
| p | Family-Wide Error rate |
|---|---|
| 2 | 0.049375 |
| 3 | 0.049171 |
| 4 | 0.049070 |
| 5 | 0.049010 |
| 10 | 0.048890 |
| 20 | 0.048830 |
| 50 | 0.048794 |
The problem with the Bonferroni Correction, however, is that it can be quite conservative when there is a correlation among the variables, particularly when doing a large number of tests. In a multivariate setting, the assumption of independence between variables is likely to be violated.
Consequence
When using the Bonferroni adjustment for many tests with correlated variables, the true family-wide error rate can be much less than \(\alpha\). These tests are conservative and there is low power to detect the desired effects.
7.1.3 - Hotelling’s T-Square
7.1.3 - Hotelling’s T-SquareA more preferable test statistic is Hotelling’s \(T^2\) and we will focus on this test.
To motivate Hotelling's \(T^2\), consider the square of the t-statistic for testing a hypothesis regarding a univariate mean. Recall that under the null hypothesis, t has a distribution with n-1 degrees of freedom. Now consider squaring this test statistic as shown below:
\[t^2 = \frac{(\bar{x}-\mu_0)^2}{s^2/n} = n(\bar{x}-\mu_0)\left(\frac{1}{s^2}\right)(\bar{x}-\mu_0) \sim F_{1, n-1}\]
When you square a t-distributed random variable with n-1 degrees of freedom, the result is an F-distributed random variable with 1 and n-1 degrees of freedom. We reject \(H_{0}\) at level \(α\) if \(t^2\) is greater than the critical value from the F-table with 1 and n-1 degrees of freedom, evaluated at level \(α\).
\(t^2 > F_{1, n-1,\alpha}\)
-
Hotelling's T-Square
-
Consider the last term in the above expression for \(t^2\). In the expression for Hotelling's \(T^2\), the difference between the sample mean and \(\mu_{0}\) is replaced with the difference between the sample mean vector and the hypothesized mean vector \(\boldsymbol{\mu _{0}}\). The inverse of the sample variance is replaced by the inverse of the sample variance-covariance matrix S, yielding the expression below:
\(T^2 = n\mathbf{(\overline{X}-\mu_0)'S^{-1}(\overline{X}-\mu_0)}\)
Notes on \(\mathbf{T^2}\)
For large n, \(T^2\) is approximately chi-square distributed with p degrees of freedom.
If we replace the sample variance-covariance matrix, S, with the population variance-covariance matrix, \(Σ\)
\(n\mathbf{(\overline{X}-\mu_0)'\Sigma^{-1}(\overline{X}-\mu_0)},\)
then the resulting test is exactly chi-square distributed with p degrees of freedom when the data are normally distributed.
For small samples, the chi-square approximation for \(T^2\) does not take into account variation due to estimating \(Σ\) with the sample variance-covariance matrix S.
Better results can be obtained from the transformation of the Hotelling \(T^2\) statistic as below:
\[F = \frac{n-p}{p(n-1)}T^2 \sim F_{p,n-p}\]
Under the null hypothesis, \(H_{0}\colon \boldsymbol{\mu} = \boldsymbol{\mu_{0}}\), this will have an F distribution with p and n-p degrees of freedom. We reject the null hypothesis, \(H_{0}\), at level \(α\) if the test statistic F is greater than the critical value from the F-table with p and n-p degrees of freedom, evaluated at level \(α\).
\(F > F_{p, n-p, \alpha}\)
To illustrate the Hotelling's \(T^2\) test we will return to the USDA Women’s Health Survey data.
7.1.4 - Example: Women’s Survey Data and Associated Confidence Intervals
7.1.4 - Example: Women’s Survey Data and Associated Confidence IntervalsExample 7-1: Woman's Survey Data (Hotelling's \(T^{2}\) Test)
The data are stored in the file that can be downloaded: nutrient.csv
The Hotelling's \(T^{2}\) test is calculated using the SAS program as shown below.
It turns out that SAS does not have any procedures for calculating Hotelling's \(T^{2}\). So, in this case, we are going to have to rely on the simple procedure, which can carry out matrix manipulation. And in this case, it can be used for carrying out Hotelling's \(T^{2}\) test.
Download the SAS Program: nutrient4.sas
To use this program, I recommend copying the program here and then making the necessary changes to use it with your dataset on your homework assignment. Again, only three entries are all we really need to change to use this with any dataset. First the specified value of μo. Second, which dataset you want to use, and third, the specification of what variable you want to analyze.
Download the results printed in the output: nutrient4.lst.
Explore the code below to see how to find the Hotelling's \(T^2\) value using the SAS statistical software application.
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Hotellings T2 - Women's Nutrition Data";
data nutrient;
infile "D:\Statistics\STAT 505\data\nutrient.csv" firstobs=2 delimiter=',';
input id calcium iron protein a c;
run;
/* iml code to compute the hotelling t2 statistic
* hotel is the name of the module we define here
* mu0 is the null vector
* one is a vector of 1s
* ident is the identity matrix
* ybar is the vector of sample means
* s is the sample covariance matrix
* t2 is the squared statistical distance between ybar and mu0
* f is the final form of the t2 statistic after scaling
* to have an f-distribution
* the module definition is ended with the 'finish' statement
* use nutrient makes the data set 'nutrient' available
* the variables from nutrient are input to x and hotel module is called
*/
proc iml;
start hotel;
mu0={1000, 15, 60, 800, 75};
one=j(nrow(x),1,1);
ident=i(nrow(x));
ybar=x`*one/nrow(x);
s=x`*(ident-one*one`/nrow(x))*x/(nrow(x)-1.0);
print mu0 ybar;
print s;
t2=nrow(x)*(ybar-mu0)`*inv(s)*(ybar-mu0);
f=(nrow(x)-ncol(x))*t2/ncol(x)/(nrow(x)-1);
df1=ncol(x);
df2=nrow(x)-ncol(x);
p=1-probf(f,df1,df2);
print t2 f df1 df2 p;
finish;
use nutrient;
read all var{calcium iron protein a c} into x;
run hotel;
Finding the Hotelling's T2 value
To calculate the one-sample Hotelling T2 statistic:
- Open the ‘nutrient’ data set in a new worksheet.
- Stat > Basic Statistics > Store Descriptive Statistics
- Highlight and select all five variables (calcium through vitamin C) to move them to the Variables window.
- Under Statistics, choose ‘Mean’, and then ‘OK’.
- Choose ‘OK’ again. The five variable means are displayed in five new columns in the worksheet.
- Data > Transpose Columns
- Highlight and select the five column names with the means from the step above.
- Choose ‘After last column in use’ then ‘OK'. The means are displayed in a single column in the worksheet.
- Name the new column of the numeric means ‘means’ for the remaining steps.
- Name a new column in the worksheet ‘mu0’ and input the values for the null hypothesis in the first five rows: 1000, 15, 60, 800, and 75. The order of these should correspond to the order of the variable means from step 4.
- Name a new column in the worksheet ‘diff’
- Calc > Calculator
- Choose ‘diff’ for the Store result window.
- In the expression window enter 'means' - 'mu0' and then ‘OK’. The five differences are displayed in the worksheet in the ‘diff’ column.
- Data > Copy > Columns to Matrix
- Highlight and select ‘diff’ for the Copy from the columns window.
- Enter the ‘M1’ in the In current worksheet window. Then choose ‘OK’.
- Calc > Matrices > Transpose
- Highlight and select ‘M1’ in the Transpose from the window and enter ‘M2’ in the 'Store result' window.
- Choose ‘OK’.
- Stat > Basic Statistics > Covariance
- Highlight and select all five variables (calcium through vitamin C) to move them to the Variables window.
- Check the box to Store matrix and then choose ‘OK’. This will store the covariance matrix in a new variable ‘M3’.
- Calc > Matrices > Invert
- Highlight and select ‘M3’ to move it to the Invert from the window.
- Enter ‘M4’ in the 'Store result in' window and choose ‘OK’. This will store the inverted covariance matrix in a new variable ‘M4’.
- Calc > Matrices > Arithmetic
- Choose Multiply and enter M2 and M4, respectively in the two windows.
- Enter ‘M5’ as the name in the 'Store result' window and then ‘OK’.
- Calc > Matrices > Arithmetic
- Choose Multiply and enter M5 and M1, respectively in the two windows.
- Enter ‘M6’ as the name in the Store result window and then ‘OK’. The answer 2.3861 is displayed in the results window.
- Calc > Calculator
- Enter C16 (or any unused column name) in the 'Store result' window.
- In the Expression window, enter 2.3861 * 737 (this is the answer from 13b times the sample size). Choose ‘OK’. The value of the T2 statistic is displayed in the worksheet under ‘C16’.
Analysis
The recommended intake and sample mean are given below
| Variable | Recommended Intake (\(μ_{o}\)) | Mean |
|---|---|---|
| Calcium | 1000 mg | 624.0 mg |
| Iron | 15mg | 11.1 mg |
| Protein | 60g | 65.8 g |
| Vitamin A | 800 μg | 839.6 μg |
| Vitamin C | 75 mg | 78.9 mg |
as well as the sample variance-covariance matrix:
\(S = \left(\begin{array}{rrrrr}157829.4 & 940.1 & 6075.8 & 102411.1 & 6701.6 \\ 940.1 & 35.8 & 114.1 & 2383.2 & 137.7 \\ 6075.8 & 114.1 & 934.9 & 7330.1 & 477.2 \\ 102411.1 & 2383.2 & 7330.1 & 2668452.4 & 22063.3 \\ 6701.6 & 137.7 & 477.2 & 22063.3 & 5416.3 \end{array}\right)\)
Hotelling’s T-square comes out to be:
\(T^2 = 1758.54\)
The F-statistic is:
\(F = 349.80 > 3.042 = F_{5,732,0.01}\)
For an 0.01 level test, the critical value is approximately 3.02. Because 349.80 is greater than this value, we can reject the null hypothesis that the average dietary intake meets recommendations.
\((T^2 = 1758.54; F = 349.80; d.f. = 5,732; p < 0.0001)\)
The SAS program reports the p-value as 0.00. In this case, the p-values can never equal zero. It is preferable to state that the p-value is less than 0.0001.
Conclusion
For all women between 25 and 50 years old, the average dietary intake does not meet recommended standards. Returning to the table of sample means and recommended dietary intake, it appears that women fail to meet nutritional standards for calcium and iron, and perhaps exceed intakes for protein, vitamin A, and vitamin C.
Such a statement, however, is not entirely backed up by the evidence.
A Question Emerges...
For which nutrients do women fall significantly below recommended nutritional intake levels? Or, conversely, for what nutrients do women fall significantly above recommended nutritional intake levels?
A naive approach to addressing the above is to calculate Confidence Intervals for each of the nutritional intake levels, one at a time, using the univariate method as shown below:
\(\bar{x}_j \pm t_{n-1, \alpha/2} \sqrt{s^2_j/n}\)
If we consider only a single variable, we can say with \((1 - α) × 100\%\) confidence that the interval includes the corresponding population mean.
Example 7-2: Women’s Health Survey:
A one-at-a-time 95% confidence interval for calcium is given by the following where values are substituted into the formula and the calculations are worked out as shown below:
\(624.04925 \pm t_{736, 0.025}\sqrt{157829.4/737}\)
\(624.04925 \pm 1.96 \times 14.63390424\)
\(624.04925 \pm 28.68245\)
\((595.3668, 652.7317)\)
The one-at-a-time confidence intervals are summarized in the table below:
| Variable | \(μ_{0}\) | 95% Confidence Interval |
|---|---|---|
| Calcium | 1000 mg | 595.3, 652.8 |
| Iron | 15mg | 10.7, 11.6 |
| Protein | 60g | 63.6, 68.0 |
| Vitamin A | 800 μg | 721.5, 957.8 |
| Vitamin C | 75 mg | 73.6, 84.2 |
Looking at this table, it appears that the average daily intakes of calcium and iron are too low (because the intervals fall below the recommended intakes of these variables), and the average daily intake of protein is too high (because the interval falls above the recommended intake of protein).
Problem: The problem with these one-at-a-time intervals is that they do not control for a family-wide error rate.
Consequence: We are less than 95% confident that all of the intervals simultaneously cover their respective means.
To fix this problem we can calculate a \((1 - \alpha) × 100\%\) Confidence Ellipse for the population mean vector \(\boldsymbol{\mu}\). To calculate this confidence ellipse we must recall that for independent random observations from a multivariate normal distribution with mean vector \(\mu\) and variance-covariance matrix \(Σ\), the F-statistic, (shown below), is F-distributed with p and n-p degrees of freedom:
\(F = n\mathbf{(\bar{x} - \boldsymbol{\mu})'S^{-1}(\bar{x} - \boldsymbol{\mu})}\dfrac{(n-p)}{p(n-1)} \sim F_{p,n-p}\)
This next expression says that the probability that n times the squared Mahalanobis distance between the sample mean vector, \(\boldsymbol{\bar{x}}\), and the population mean vector \(\boldsymbol{\mu}\) is less than or equal to p times n-1 times the critical value from the F-table divided by n-p is equal to \(1 - α\).
\(\text{Pr}\{n\mathbf{(\bar{x} - \boldsymbol{\mu})'S^{-1}(\bar{x} - \boldsymbol{\mu})} \le \dfrac{p(n-1)}{(n-p)}F_{p,n-p,\alpha}\} = 1-\alpha\)
Here the squared Mahalanobis distance between \(\bar{\mathbf{x}}\) and \(\boldsymbol{\mu}\) is being used.
Note! A closely-related equation for a hyper-ellipse is:
\(n\mathbf{(\bar{x} -\boldsymbol{\mu})'S^{-1}(\bar{x} - \boldsymbol{\mu})} = \dfrac{p(n-1)}{(n-p)}F_{p,n-p, \alpha}\)
In particular, this is the \((1 - \alpha) × 100%\) confidence ellipse for the population mean, \(\boldsymbol{\mu}\).
Interpretation
The \((1 - \alpha) × 100\%\) confidence ellipse is very similar to the prediction ellipse that we discussed earlier in our discussion of the multivariate normal distribution. A \((1 - \alpha) × 100\%\) confidence ellipse yields simultaneous \((1 - \alpha) × 100\%\) confidence intervals for all linear combinations of the variable means. Consider linear combinations of population means as below:
\(c_1\mu_1 + c_2\mu_2 + \dots c_p \mu_p = \sum_{j=1}^{p}c_j\mu_j = \mathbf{c'\boldsymbol{\mu}}\)
The simultaneous \((1 - \alpha) × 100\%\) confidence intervals for the above are given by the expression below
\(\sum_{j=1}^{p}c_j\bar{x}_j \pm \sqrt{\frac{p(n-1)}{(n-p)}F_{p, n-p, \alpha}}\sqrt{\frac{1}{n}\sum_{j=1}^{p}\sum_{k=1}^{p}c_jc_ks_{jk}}\)
In terms of interpreting the \((1 - \alpha) × 100\%\) confidence ellipse, we can say that we are \((1 - \alpha) × 100%\) confident that all such confidence intervals cover their respective linear combinations of the treatment means, regardless of what linear combinations we may wish to consider. In particular, we can consider the trivial linear combinations which correspond to the individual variables. So this says that we going to be also \((1 - \alpha) × 100\%\) confident that all of the intervals given in the expression below:
\(\bar{x}_j \pm \sqrt{\frac{p(n-1)}{(n-p)}F_{p, n-p, \alpha}}\sqrt{\frac{s^2_j}{n}}\)
cover their respective treatment population means. These intervals are called simultaneous confidence intervals.
Example 7-3: Women’s Health Survey
Simultaneous confidence intervals are computed using hand calculations. For calcium, we substituted the following values: The sample mean was 624.04925. We have p = 5 variables, a total sample size of n = 737, and if we look up in the F-table for 5 and 732 degrees of freedom for alpha = 0.05, the critical value is 2.21. The standard error of the sample mean for calcium is equal to the square root of the sample variance for calcium, 157,829.44, divided by the sample size, 737. The math is carried out to obtain an interval running from 575.27 to approximately 672.83 as shown below:
\(624.04925 \pm \sqrt{\frac{5(737-1)}{737-5}\underset{2.21}{\underbrace{F_{5,737-5,0.05}}}}\sqrt{157829.4/737}\)
\(624.04925 \pm 3.333224 \times 14.63390424\)
\(624.04925 \pm 48.77808\)
\((575.27117, 672.82733)\)
These calculations may also be carried out using the SAS program.
SAS Program can be downloaded: nutrient5.sas
In terms of using this program, there is only a couple of things you need to change: the value of p in line five and what appears in the data step at the top of the page.
Explore the code below to see how to find the Hotelling's \(T^2\) value using the SAS statistical software application.
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Confidence Intervals - Women's Nutrition Data";
/* %let allows the p variable to be used throughout the code below
* After reading in the nutrient data, where each variable is
* originally in its own column, the next statements stack the data
* so that all variable names are in one column called 'variable',
* and all response values are in another column called 'x'.
* This format is used for the calculations that follow.
*/
%let p=5;
data nutrient;
infile "D:\Statistics\STAT 505\data\nutrient.csv" firstobs=2 delimiter=',';
input id calcium iron protein a c;
variable="calcium"; x=calcium; output;
variable="iron"; x=iron; output;
variable="protein"; x=protein; output;
variable="vit a"; x=a; output;
variable="vit c"; x=c; output;
keep variable x;
run;
proc sort;
by variable;
run;
/* The means procedure calculates and saves the sample size,
* mean, and variance for each variable. It then saves these results
* in a new data set 'a' for use in the final step below.
* /
proc means noprint;
by variable;
var x;
output out=a n=n mean=xbar var=s2;
run;
/* The data step here is used to calculate the confidence interval
* limits from the statistics calculated in the data set 'a'.
* The values 't1', 'tb', and 'f' are the critical values used in the
* one-at-a-time, Bonferroni, and F intervals, respectively.
* /
data b;
set a;
t1=tinv(1-0.025,n-1);
tb=tinv(1-0.025/&p,n-1);
f=finv(0.95,&p,n-&p);
loone=xbar-t1*sqrt(s2/n);
upone=xbar+t1*sqrt(s2/n);
losim=xbar-sqrt(&p*(n-1)*f*s2/(n-&p)/n);
upsim=xbar+sqrt(&p*(n-1)*f*s2/(n-&p)/n);
lobon=xbar-tb*sqrt(s2/n);
upbon=xbar+tb*sqrt(s2/n);
run;
proc print data=b;
run;
In terms of using the program with other datasets, basically what you need to do is create a separate line starting with the variable for each variable that is included in the analysis. In this case, we have five nutritional variables so we have five of these lines in the first data step. Then you set this equal to, in quotes, the name you wish to give that variable. After the semicolon, we set x = to the name that we specified for that variable in the input statement and finally after another semicolon, we type in "output;".
The output is available to download here: nutrient5.lst.
The output contains the sample means for each of the variables, and gives the results of the calculations under data step "b".
Confidence intervals are given by the columns for "losim" and "upsim"
Minitab does not support this function.
The following table gives the confidence intervals:
| Variable | \(μ_{0}\) | 95% Confidence Interval |
|---|---|---|
| Calcium | 1000 mg | 575.1, 673.0 |
| Iron | 15 mg | 10.4, 11.9 |
| Protein | 60 g | 62.0, 69.6 |
| Vitamin A | 800 μg | 638.3, 1040.9 |
| Vitamin C | 75 mg | 69.9, 88.0 |
Looking at these simultaneous confidence intervals we can see that the upper bound of the interval for calcium falls below the recommended daily intake of 1000 mg. Similarly, the upper bound for iron also falls below the recommended daily intake of 15 mg. Conversely, the lower bound for protein falls above the recommended daily intake of 60 g of protein. The intervals for both vitamins A and C both contain the recommended daily intake for these two vitamins.
Therefore, we can conclude that the average daily intake of calcium and iron fall below the recommended levels, and the average daily intake of protein exceeds the recommended level.
Problem with Simultaneous Confidence Intervals
The problem with the simultaneous confidence intervals is that if we are not interested in all possible linear combinations of variables or anything other than the means by themselves, then the simultaneous confidence interval may be too wide, and hence, too conservative. As an alternative to the simultaneous confidence intervals, we can use the Bonferroni intervals.
Bonferroni Intervals
The Bonferroni intervals are given in the expression below:
\(\bar{x}_j \pm t_{n-1, \frac{\alpha}{2p}}\sqrt{s^2_j/n}\)
An example from the USDA Women’s Health Survey data will illustrate this calculation.
Example 7-4: Women’s Health Survey
Here, the 95% confidence interval for calcium under the Bonferroni correction is calculated:
\(624.04925 \pm t_{737-1, \frac{0.05}{2 \times 5}}\sqrt{157829.4/737}\)
\(624.04925 \pm 2.576 \times 14.63390424\)
\(624.04925 \pm 37.69694\)
\((586.35231, 661.74619)\)
This calculation uses the values for the sample mean for calcium, 624.04925, the critical value from the t-table, with n-1 degrees of freedom, evaluated at alpha over 2 times p, (0.05 divided 2 times 5, or .005). This critical value turns out to be 2.576 from the t-table. The standard error is calculated by taking the square root of the sample variance, (157,829.44), divided by the sample size, 737.
Carrying out the math, the interval goes from 586.35 to 661.75.
These calculations can also be obtained in the SAS program with the downloadable code below. The calculations of the upper and lower Bonferroni intervals are given by "lobon" and "upbon" at the end of data step "b". They involve the calculations:
lobon=xbar-tb*sqrt(s2/n);
upbon=xbar+tb*sqrt(s2/n);
SAS Program can be downloaded here: nutrient5.sas
At this time Minitab does not support this procedure.
The table below shows the results of the computation
| Variable | \(\mu_{0}\) | 95% Confidence Interval |
|---|---|---|
| Calcium | 1000 mg | 586.3, 661.8 |
| Iron | 15mg | 10.6, 11.7 |
| Protein | 60g | 62.9, 68.7 |
| Vitamin A | 800 μg | 684.2, 995.0 |
| Vitamin C | 75 mg | 71.9, 85.9 |
When compared to the simultaneous intervals, we see that the Bonferroni intervals are narrower. However, in this case, the conclusions will be the same. The confidence intervals for both vitamins A and C both cover their respective recommended daily intakes. Intervals for calcium and iron fall below the recommended intake, while the interval for protein falls above it.
7.1.5 - Profile Plots
7.1.5 - Profile PlotsIf the data is of a very large dimension, tables of simultaneous or Bonferroni confidence intervals are hard to grasp at a cursory glance. A better approach is to visualize the coverage of the confidence intervals through a profile plot.
Procedure
A profile plot is obtained with the following three-step procedure:
Steps
- Standardize each of the observations by dividing them by their hypothesized means. So the \(i^{th}\) observation of the \(j^{th}\) variable, \(X_{ij}\), is divided by its hypothesized mean for\(j^{th}\) variable \(\mu_0^j\). We will call the result \(Z_{ij}\) as shown below:
\(Z_{ij} = \dfrac{X_{ij}}{\mu^0_j}\)
-
Compute the sample mean for the \(Z_{ij}\)'s to obtain sample means corresponding to each of the variables j, 1 to p. These sample means, \(\bar{z_j}\), are then plotted against the variable j.
-
Plot either simultaneous or Bonferroni confidence bands for the population mean of the transformed variables,
Simultaneous \((1 - α) × 100\%\) confidence bands are given by the usual formula, using the z's instead of the usual x's as shown below:
\(\bar{z}_j \pm \sqrt{\dfrac{p(n-1)}{(n-p)}F_{p,n-p,\alpha}}\sqrt{\dfrac{s^2_{Z_j}}{n}}\)
The same substitutions are made for the Bonferroni \((1 - α) × 100\%\) confidence band formula:
\(\bar{z}_j \pm t_{n-1,\frac{\alpha}{2p}}\sqrt{\dfrac{s^2_{Z_j}}{n}}\)
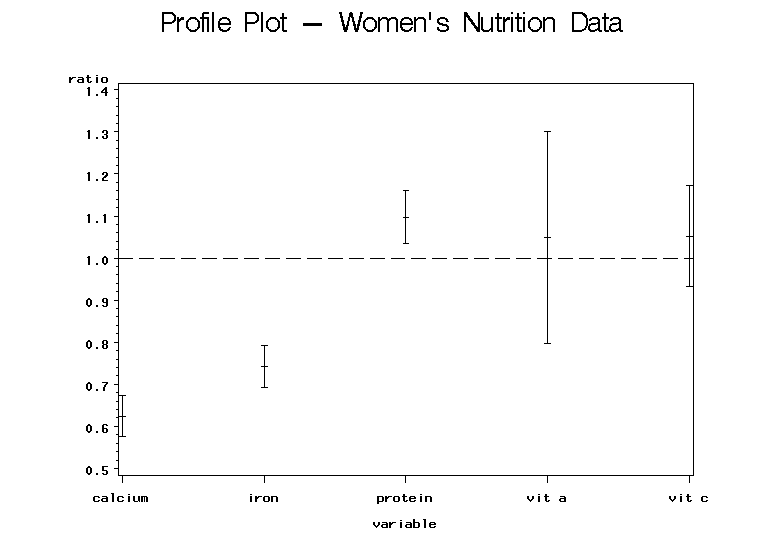
Example 7-5: Women's Health Survey (Profile Plots)
The profile plots are computed using the SAS program.
Download the SAS Program: nutrient6.sas
Explore the code below to see how to create a profile plot using the SAS statistical software application.
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Profile Plot - Women's Nutrition Data";
/* %let allows the p variable to be used throughout the code below
* After reading in the nutrient data, where each variable is
* originally in its own column, the next statements stack the data
* so that all variable names are in one column called 'variable',
* and all response values divided by their null values
* are in another column called 'ratio'.
* This format is used for the calculations that follow, as well
* as for the profile plot.
*/
%let p=5;
data nutrient;
infile "D:\Statistics\STAT 505\data\nutrient.csv" firstobs=2 delimiter=','
input id calcium iron protein a c;
variable="calcium"; ratio=calcium/1000; output;
variable="iron"; ratio=iron/15; output;
variable="protein"; ratio=protein/60; output;
variable="vit a"; ratio=a/800; output;
variable="vit c"; ratio=c/75; output;
keep variable ratio;
run;
proc sort;
by variable;
run;
/* The means procedure calculates and saves the sample size,
* mean, and variance for each variable. It then saves these results
* in a new data set 'a' for use in the steps below.
* /
proc means;
by variable;
var ratio;
output out=a n=n mean=xbar var=s2;
run;
/* The data step here is used to calculate the simultaneous
* confidence intervals based on the F-multiplier.
* Three values are saved for the plot: the ratio itself and
* both endpoints, lower and upper, of the confidence interval.
* /
data b;
set a;
f=finv(0.95,&p,n-&p);
ratio=xbar; output;
ratio=xbar-sqrt(&p*(n-1)*f*s2/(n-&p)/n); output;
ratio=xbar+sqrt(&p*(n-1)*f*s2/(n-&p)/n); output;
run;
/* The axis commands define the size of the plotting window.
* The horizontal axis is of the variables, and the vertical
* axis is used for the confidence limits.
* The reference line of 1 corresponds to the null value of the
* ratio for each variable.
* /
proc gplot;
axis1 length=4 in;
axis2 length=6 in;
plot ratio*variable / vaxis=axis1 haxis=axis2 vref=1 lvref=21;
symbol v=none i=hilot color=black;
run;
Creating a profile plot
To construct a profile plot with confidence limits:
- Open the ‘nutrient’ data set in a new worksheet
- Name the columns id, calcium, iron, protein, vit_A, and vit_C, from left to right.
- Name new columns R_calcium, R_iron, R_protein, R_A, and R_C for the ratios created next.
- Calc > Calculator
- Highlight and select R_calcium to move it to the Store result window.
- In the Expression window, enter ‘calcium’ / 1000, where the value 1000 comes from the null value of interest.
- Choose 'OK'. The ratios for calcium are displayed in the worksheet variable R_calcium.
- Repeat step 4. for the other 4 variables, where each new ratio is obtained by dividing the original variable by its null value.
- Graph > Interval plot > Multiple Y variables with categorical variables > OK
- Highlight and select all five ratio variables (R_calcium through R_C) to move them to the Y-variables window.
- Display Y’s > Y’s first
- Under Options, make sure the Mean confidence interval bar and Mean symbol are checked.
- Choose 'OK', then 'OK' again. The profile plot is shown in the results area.
Analysis
From this plot, the results are immediately clear. We can easily see that the confidence intervals for calcium and iron fall below 1 indicating that the average daily intakes for these two nutrients are below recommended levels. The protein confidence interval falls above the value 1 indicating that the average daily intake of protein exceeds the recommended level. The confidence intervals for vitamins A and C both contain 1 showing no significant evidence against the null hypothesis and suggesting that they meet the recommended intake of these two vitamins.
7.1.6 - Paired Hotelling's T-Square
7.1.6 - Paired Hotelling's T-SquarePaired Samples occur in a number of different situations. For example:
- Pairs of similar individuals are selected from a population. These are selected in such a way that the two members of each pair are more similar to one another than they are to different observations in the dataset. Under this setting, one treatment may be applied to a randomly selected member of each pair, while the other treatment is applied to the remaining member.
- For a single sample of individuals, measurements may be taken both before and after treatment. For example, the mineral content of six bones is measured before and after one year of diet and exercise treatments.
- Cat eye experiment: At the University of Georgia an experiment was conducted to test the effect of a treatment for glaucoma. In this experiment, a treatment for glaucoma is applied to a randomly selected eye of each cat, while the remaining eye received a placebo. Many measurements were taken on each eye including pressure, dilation, etc.
The example that we are going to consider in this lesson involves spouse data. In this case, we have husband and wife pairs.
Example 7-6: Spouse Data
A sample of husband and wife pairs are asked to respond to each of the following questions:
- What is the level of passionate love you feel for your partner?
- What is the level of passionate love your partner feels for you?
- What is the level of companionate love you feel for your partner?
- What is the level of companionate love your partner feels for you?
A total of 30 married couples were questioned. Responses were recorded on a five-point scale. Responses included the following values:
- None at all
- Very little
- Some
- A great deal
- Tremendous amount
We will try to address two separate questions from these data.
- Do the husbands respond to the questions in the same way as their wives?
- Do the husbands and wives accurately perceive the responses of their spouses?
We shall address Question 1 first...
7.1.7 - Question 1: The Univariate Case
7.1.7 - Question 1: The Univariate CaseExample 7-7: Spouse Data (Question 1)
Question 1: Do the husbands respond to the questions in the same way as their wives?
Before considering the multivariate case let's review the univariate approach to answering this question. In this case, we will compare the responses to a single question.
Univariate Paired t-test Case: Consider comparing the responses to a single question.
A notation will be as follows:
- \(X _ { 1 i }\) = response of husband i - the first member of pair i
- \(X _ { 2 i }\) = response of wife i - the second member of pair i
- \(\mu _ { 1 }\) = population mean for the husbands - the first population
- \(\mu _ { 2 }\) = population mean for the wives - the second population
Our objective here is to test the null hypothesis that the population means are equal against the alternative hypothesis that means are not equal, as described in the expression below:
\(H_0\colon \mu_1 =\mu_2 \) against \(H_a\colon \mu_1 \ne \mu_2\)
In the univariate course, you learned that the null hypothesis is tested as follows. First, we define \(Y _ { i }\) to be the difference in responses for the \(i^{th}\) pair of observations. In this case, this will be the difference between husband i and wife i. Likewise, we can also define \(\mu _ { Y }\) to be the population mean of these differences, which is the same as the difference between the population means \(\mu _ { 1 }\) and \(\mu _ { 2 }\), both as noted below:
\(Y_i = X_{1i}-X_{2i}\) and \(\mu_Y = \mu_1-\mu_2\)
Testing the null hypothesis for the equality of the population means is going to be equivalent to testing the null hypothesis that \(\mu _ { Y }\) is equal to 0 against the general alternative that \(\mu _ { Y }\) is not equal to 0.
\(H_0\colon \mu_Y =0 \) against \(H_a\colon \mu_Y \ne 0\)
This hypothesis is tested using the paired t-test.
We will define \(\bar{y}\) to be the sample mean of the \(Y _ { i }\)'s:
\(\bar{y} = \dfrac{1}{n}\sum_{i=1}^{n}Y_i\)
We will also define \(s_{2}Y\) to be the sample variance of the \(Y _ { i }\)'s:
\(s^2_Y = \dfrac{\sum_{i=1}^{n}Y^2_i - (\sum_{i=1}^{n}Y_i)^2/n}{n-1}\)
We will make the usual four assumptions in doing this:
- The \(Y _ { i }\)'s have common mean \(\mu _ { Y }\)
- Homoskedasticity. The \(Y _ { i }\)'s have common variance \(\sigma^2_Y\).
- Independence. The \(Y _ { i }\)'s are independently sampled.
- Normality. The \(Y _ { i }\)'s are normally distributed.
The test statistic is a t-statistic which is, in this case, equal to the sample mean divided by the standard error as shown below:
\[t = \frac{\bar{y}}{\sqrt{s^2/n}} \sim t_{n-1}\]
Under the null hypothesis, \(H _ { o }\) this test statistic is going to be t-distributed with n-1 degrees of freedom and we will reject \(H _ { o }\) at level \(α\) if the absolute value of the t-value exceeds the critical value from the t-distribution with n-1 degrees of freedom evaluated at \(α\) over 2.
\(|t| > t_{n-1, \alpha/2}\)
7.1.8 - Multivariate Paired Hotelling's T-Square
7.1.8 - Multivariate Paired Hotelling's T-SquareExample 7-8: Spouse Data (Multivariate Case)
Now let's consider the multivariate case. All scalar observations will be replaced by vectors of observations. As a result, we will use the notation that follows:
Husband:
\(\mathbf{X}_{1i} = \left(\begin{array}{c}X_{1i1}\\ X_{1i2}\\\vdots\\X_{1ip}\end{array}\right)\) = vector of observations for the \(i ^{ th } \text{ husband}\)
\(X _{ 1i1 }\) will denote the response of the \(i ^{ th }\) husband to the first question. \(X _{ 1i2 }\) will denote the response of the \(i ^{ th }\) husband to the second question and so on...
Wife:
\(\mathbf{X}_{2i} = \left(\begin{array}{c}X_{2i1}\\ X_{2i2}\\\vdots\\X_{2ip}\end{array}\right)\) = vector of observations for the \(i ^{ th } \text{ wife}\)
\(X _{ 2i1 }\) will denote the response of the \(i ^{ th }\) wife to the first question. \(X _{ 2i2 }\) will denote the response of the \(i ^{ th }\) wife to the second question and so on...
The scalar population means are replaced by the population mean vectors so that \(\mu _{ 1 }\) = population mean vector for husbands and \(\mu _{ 2 }\) = population mean vector for the wives.
Here we are interested in testing the null hypothesis that the population mean vectors are equal against the general alternative that these mean vectors are not equal.
\(H_0\colon \boldsymbol{\mu_1} = \boldsymbol{\mu_2}\) against \(H_a\colon \boldsymbol{\mu_1} \ne \boldsymbol{\mu_2}\)
Under the null hypothesis, the two mean vectors are equal element by element. As with the one-sample univariate case, we are going to look at the differences between the observations. We will define the vector \(Y _{ 1 }\) for the \(i ^{ th }\) couple to be equal to the vector \(X _{ 1i }\) for the \(i ^{ th }\) husband minus the vector \(X _{ 2i }\) for the \(i ^{ th }\) wife. Then we will also, likewise, define the vector \(\mu _{ Y }\) to be the difference between the vector \(\mu _{ 1 }\) and the vector \(\mu _{ 2 }\).
\(\mathbf{Y}_i = \mathbf{X}_{1i}-\mathbf{X}_{2i}\) and \(\boldsymbol{\mu}_Y = \boldsymbol{\mu}_1-\boldsymbol{\mu}_2\)
Testing the above null hypothesis is going to be equivalent to testing the null hypothesis that the population mean vector \(\mu _{ Y }\) is equal to 0. That is, all of its elements are equal to 0. This is tested against the alternative that the vector \(\mu _{ Y }\) is not equal to 0, that is at least one of the elements is not equal to 0.
\(H_0\colon \boldsymbol{\mu}_Y = \mathbf{0}\) against \(H_a\colon \boldsymbol{\mu}_Y \ne \mathbf{0}\)
This hypothesis is tested using the paired Hotelling's \(T^{ 2 }\) test.
As before, we will define \(\mathbf{\bar{Y}}\) to denote the sample mean vector of the vectors \(Y_{ i }\).
\(\mathbf{\bar{Y}} = \dfrac{1}{n}\sum_{i=1}^{n}\mathbf{Y}_i\)
And, we will define \(S _{ Y }\) to denote the sample variance-covariance matrix of the vectors \(Y_{ i }\).
\(\mathbf{S}_Y = \dfrac{1}{n-1}\sum_{i=1}^{n}\mathbf{(Y_i-\bar{Y})(Y_i-\bar{Y})'}\)
The assumptions are similar to the assumptions made for the one-sample Hotelling's T-square test:
- The vectors \(Y _{ 1 }\)'s have a common population mean vector \(\mu _{ Y }\), which essentially means that there are no sub-populations with mean vectors.
- The vectors \(Y _{ 1 }\)'s have common variance-covariance matrix \(\Sigma_Y\).
- Independence. The \(Y _{ 1 }\)'s are independently sampled. In this case, independence among the couples in this study.
- Normality. The \(Y _{ 1 }\)'s are multivariate normally distributed.
Paired Hotelling's T-Square test statistic is given by the expression below:
\(T^2 = n\bar{\mathbf{Y}}'\mathbf{S}_Y^{-1}\mathbf{\bar{Y}}\)
It is a function of sample size n, the sample mean vectors, \(\mathbf{\bar{Y}}\), and the inverse of the variance-covariance matrix \(\mathbf{S} _{ Y }\).
Then we will define an F-statistic as given in the expression below:
\(F = \dfrac{n-p}{p(n-1)}T^2 \sim F_{p, n-p}\)
Under the null hypothesis, \(H _{ o } \colon \mu _{ Y } = 0\), this will have an F-distribution with p and n-p degrees of freedom. We will reject \(H _{ o }\) at level \(\alpha\) if the F-value exceeds the value from F-value with p and n-p degrees of freedom, evaluated at level \(\alpha\).
\(F > F_{p,n-p,\alpha}\)
Let us return to our example...
7.1.9 - Example: Spouse Data
7.1.9 - Example: Spouse DataExample 7-9: Spouse Data (Paired Hotelling's)
Download the text file containing the data here: spouse.csv
The Spouse Data may be analyzed using the SAS program as shown below:
Download the SAS Program: spouse.sas
Explore the code below to see how to compute the Paired Hotelling's \(T^2\) using the SAS statistical software application.
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Paired Hotelling's T-Square";
/* The differences 'd1' through 'd4' are defined
* and added to the data set.
*/
data spouse;
infile "D:\Statistics\STAT 505\data\spouse.csv" firstobs=2 delimiter=',';
input h1 h2 h3 h4 w1 w2 w3 w4;
d1=h1-w1;
d2=h2-w2;
d3=h3-w3;
d4=h4-w4;
run;
proc print data=spouse;
run;
/* The iml code below defines and executes the 'hotel' module
* for calculating the one-sample Hotelling T2 test statistic.
* The calculations are based on the differences, which is why
* there is a single null vector consisting of only 0s.
* The commands between 'start' and 'finish' define the
* calculations of the module for an input vector 'x'.
* The 'use' statement makes the 'spouse' data set available, from
* which the difference variables are taken. The difference variables
* are then read into the vector 'x' before the 'hotel' module is called.
*/
proc iml;
start hotel;
mu0={0, 0, 0, 0};
one=j(nrow(x),1,1);
ident=i(nrow(x));
ybar=x`*one/nrow(x);
s=x`*(ident-one*one`/nrow(x))*x/(nrow(x)-1.0);
print mu0 ybar;
print s;
t2=nrow(x)*(ybar-mu0)`*inv(s)*(ybar-mu0);
f=(nrow(x)-ncol(x))*t2/ncol(x)/(nrow(x)-1);
df1=ncol(x);
df2=nrow(x)-ncol(x);
p=1-probf(f,df1,df2);
print t2 f df1 df2 p;
finish;
use spouse;
read all var{d1 d2 d3 d4} into x;
run hotel;
The downloadable output is given by spouse.lst.
The first page of the output just gives a list of the raw data. You can see all of the data are numbers between 1 and 5. If you look at them closely, you can see that they are mostly 4's and 5's, a few 3's. I don't think we see a 1 in there are all.
You can also see the columns for d1 through d4, and you should be able to confirm that they are indeed equal to the differences between the husbands' and wives' responses to the four questions.
The second page of the output gives the results of the iml procedure. First, it gives the hypothesized values of the population mean under the null hypothesis. In this case, it is just a column of zeros. The sample means of the differences are given in the next column. So the mean of the differences between the husband and wife's response to the first question is 0.0666667. This is also copied into the table below. The differences for the next three questions follow.
Following the sample mean vector is the sample variance-covariance matrix. The diagonal elements give the sample variances for each of the questions. So, for example, the sample variance for the first question is 0.8229885, which we have rounded off to 0.8230 and copied into the table below as well. The second diagonal element gives the sample variance for the second question, and so on.
The results of Hotelling's T-square statistic are given at the bottom of the output page.
Computing the paired Hotelling's T2
To calculate the paired Hotelling T2 statistic:
- Open the ‘spouse’ data set in a new worksheet.
- Name the columns h1, h2, h3, h4, w1, w2, w3, and w4, from left to right.
- Name new columns diff1, diff2, diff3, and diff4.
- Calc > Calculator
- Highlight and select diff1 to move it to the Store result window.
- In the Expression window, enter ‘h1’ - ‘w1’.
- Choose 'OK'. The first difference is created in the worksheet.
- Repeat step 4. for each of the other 3 differences.
- Stat > Basic Statistics > Store Descriptive Statistics
- Highlight and select all 4 difference variables (diff1 through diff4) to move them to the Variables window.
- Under Statistics, choose ‘Mean’, and then ‘OK’.
- Choose ‘OK’ again. The 4 different means are displayed in new columns in the worksheet.
- Data > Transpose Columns
- Highlight and select the 4 column names with the means from the step above.
- Choose ‘After last column in use’ then ‘OK'. The means are displayed in a single column in the worksheet.
- Name the new column of the numeric means ‘means’ for the remaining steps.
- Data > Copy > Columns to Matrix
- Highlight and select ‘means’ for the Copy from the columns window.
- Enter the ‘M1’ in the In current worksheet window. Then choose ‘OK’.
- Calc > Matrices > Transpose
- Highlight and select ‘M1’ in the 'Transpose from' window and enter ‘M2’ in the 'Store result' window.
- Choose ‘OK’.
- Stat > Basic Statistics > Covariance
- Highlight and select all 4 difference variables (diff1 through diff4) to move them to the Variables window.
- Check the box to Store matrix and then choose ‘OK’. This will store the covariance matrix in a new variable ‘M3’.
- Calc > Matrices > Invert
- Highlight and select ‘M3’ to move it to the Invert from the window.
- Enter ‘M4’ in the 'Store result in' window and choose ‘OK’. This will store the inverted covariance matrix in a new variable ‘M4’.
- Calc > Matrices > Arithmetic
- Choose Multiply and enter M2 and M4, respectively in the two windows.
- Enter ‘M5’ as the name in the Store result window and then ‘OK’.
- Calc > Matrices > Arithmetic
- Choose Multiply and enter M5 and M1, respectively in the two windows.
- Enter ‘M6’ as the name in the Store result window and then ‘OK’. The answer 0.4376 is displayed in the results window.
- Calc > Calculator
- Enter C16 (or any unused column name) in the Store result window.
- In the Expression window, enter 0.4376 * 30 (this is the answer from 14b times the sample size). Choose ‘OK’. The value of the T2 statistic is displayed in the worksheet under ‘C16’.
Analysis
The sample variance-covariance matrix from the output of the SAS program:
\(\mathbf{S} =\left(\begin{array}{rrrr}0.8230 & 0.0782 & -0.0138 & -0.0598 \\ 0.0782 & 0.8092 & -0.2138 & -0.1563 \\ -0.0138 & -0.2138 & 0.5621 & 0.5103 \\ -0.0598 & -0.1563 & 0.5103 & 0.6023 \end{array}\right)\)
Sample means and variances of the differences in responses between the husbands and wives.
| Question | Mean \((\bar {y})\) | Variance \((s_{Y}^{2})\) |
|---|---|---|
| 1 | 0.0667 | 0.8230 |
| 2 | -0.1333 | 0.8092 |
| 3 | -0.3000 | 0.5621 |
| 4 | -0.1333 | 0.6023 |
Here we have \(T^{2}\) = 13.13 with a corresponding F-value of 2.94, with 4 and 26 degrees of freedom. The 4 corresponds with the number of questions asked of each couple. The 26 comes from subtracting the sample size of 30 couples minus the 4 questions. The p-value for the test is 0.039.
The results of our test are that we can reject the null hypothesis that the mean difference between husband and wife responses is equal to zero.
Conclusion
Husbands do not respond to the questions in the same way as their wives (\(T^{2}\)= 13.13; F = 2.94; d.f. = 4, 26; p = 0.0394).
This indicates that husbands respond differently to at least one of the questions from their wives. It could be one question or more than one question.
The next step is to assess on which question the husband and wives differ in their responses. This step of the analysis will involve the computation of confidence intervals.
7.1.10 - Confidence Intervals
7.1.10 - Confidence IntervalsConfidence intervals for the Paired Hotelling's T-square are computed in the same way as for the one-sample Hotelling's T-square, therefore, the notes here will not be as detailed as for the one-sample. Let's review the basic procedures:
Simultaneous (1 - \(\alpha\)) × 100% Confidence Intervals for the mean differences are calculated using the expression below:
\(\bar{y}_j \pm \sqrt{\frac{p(n-1)}{n-p}F_{p,n-p,\alpha}}\sqrt{\frac{s^2_{Y_j}}{n}}\)
Bonferroni (1 - \(\alpha\)) × 100% Confidence Intervals for the mean differences are calculated using the following expression:
\(\bar{y}_j \pm t_{n-1, \frac{\alpha}{2p}}\sqrt{\frac{s^2_{Y_j}}{n}}\)
As before, simultaneous intervals will be used if we are potentially interested in confidence intervals for linear combinations among the variables of the data. Bonferroni intervals should be used if we want to simply focus on the means for each of the individual variables themselves. In this case, the individual questions.
Example 7-10: Spouse Data (Bonferroni CI)
The simultaneous Bonferroni Confidence intervals may be computed using the SAS program that can be downloaded below:
Download the Spouse 1 SAS Program: spouse1a.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Confidence Intervals - Spouse Data";
/* %let allows the p variable to be used throughout the code below
* After reading in the spouse data, where each variable is
* originally in its own column, the next statements define difference
* variables between husbands and wives, and they stack the data
* so that all group labels (1 through 4) are in one column called 'variable',
* and all differences are in another column called 'diff'.
* This format is used for the calculations that follow.
*/
%let p=4;
data spouse;
infile "D:\Statistics\STAT 505\data\spouse.csv" firstobs=2 delimiter=',';
input h1 h2 h3 h4 w1 w2 w3 w4;
variable=1; diff=h1-w1; output;
variable=2; diff=h2-w2; output;
variable=3; diff=h3-w3; output;
variable=4; diff=h4-w4; output;
drop h1 h2 h3 h4 w1 w2 w3 w4;
run;
proc sort;
by variable;
run;
/* The means procedure calculates and saves the sample size,
* mean, and variance for each variable. It then saves these results
* in a new data set 'a' for use in the final step below.
*/
proc means data=spouse noprint;
by variable;
var diff;
output out=a n=n mean=xbar var=s2;
run;
/* The data step here is used to calculate the confidence interval
* limits from the statistics calculated in the data set 'a'.
* The values 't' and'f' are the critical values used in the
* Bonferroni and F intervals, respectively.
*/
data b;
set a;
f=finv(0.95,&p,n-&p);
t=tinv(1-0.025/&p,n-1);
losim=xbar-sqrt(&p*(n-1)*f*s2/(n-&p)/n);
upsim=xbar+sqrt(&p*(n-1)*f*s2/(n-&p)/n);
lobon=xbar-t*sqrt(s2/n);
upbon=xbar+t*sqrt(s2/n);
run;
proc print data=b;
run;
In this output losim and upsim give the lower and upper bounds for the simultaneous intervals, and lobon and upbon give the lower and upper bounds for the Bonferroni interval which are copied into the table below. You should be able to find where all of these numbers are obtained.
Computing the Bonferroni CIs
To calculate Bonferroni confidence intervals for the paired differences:
- Open the ‘spouse’ data set in a new worksheet.
- Name the columns h1, h2, h3, h4, w1, w2, w3, and w4, from left to right.
- Name new columns diff1, diff2, diff3, and diff4.
- Calc > Calculator
- Highlight and select 'diff1' to move it to the 'Store result' window.
- In the Expression window, enter ‘h1’ - ‘w1’.
- Choose 'OK'. The first difference is created in the worksheet.
- Repeat step 4. for each of the other 3 differences.
- Calc > Basic Statistics > 1-sample t
- Choose ‘One or more sample’ in the first window.
- Highlight and select the 4 differences (diff1 through diff4) move them into the window on the right.
- Under ‘Options’, enter 98.75, which corresponds to 1-0.05/4, the adjusted individual confidence level for simultaneous 95% confidence with the Bonferroni method.
- Select Mean not equal to hypothesized mean.
- Select 'OK' twice. The 95% Bonferroni intervals are displayed in the results area.
Analysis
|
Question
|
Simultaneous
|
Bonferroni
|
|---|---|---|
|
1
|
-0.5127, 0.6460
|
-0.3744, 0.5078
|
|
2
|
-0.7078, 0.4412
|
-0.5707, 0.3041
|
|
3
|
-0.7788, 0.1788
|
-0.6645, 0.0645
|
|
4
|
-0.6290, 0.3623
|
-0.5107, 0.2440
|
The simultaneous confidence intervals are plotted using Profile Plots.
The downloadable SAS program for the profile plot can be obtained here: spouse1.sas.
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Profile Plot - Spouse Data";
/* %let allows the p variable to be used throughout the code below
* After reading in the spouse data, where each variable is
* originally in its own column, the next statements define difference
* variables between husbands and wives, and they stack the data
* so that all group labels (1 through 4) are in one column called 'variable',
* and all differences are in another column called 'diff'.
* This format is used for the calculations that follow.
*/
%let p=4;
data spouse;
infile "D:\Statistics\STAT 505\data\spouse.csv" firstobs=2 delimiter=','
input h1 h2 h3 h4 w1 w2 w3 w4;
variable=1; diff=h1-w1; output;
variable=2; diff=h2-w2; output;
variable=3; diff=h3-w3; output;
variable=4; diff=h4-w4; output;
drop h1 h2 h3 h4 w1 w2 w3 w4;
run;
proc sort;
by variable;
run;
/* The means procedure calculates and saves the sample size,
* mean, and variance for each variable. It then saves these results
* in a new data set 'a' for use in the final step below.
* /
proc means data=spouse;
by variable;
var diff;
output out=a n=n mean=xbar var=s2;
run;
/* The data step here is used to calculate the simultaneous
* confidence intervals based on the F-multiplier
* from the statistics calculated in the data set 'a'.
* /
data b;
set a;
f=finv(0.95,&p,n-&p);
diff=xbar; output;
diff=xbar-sqrt(&p*(n-1)*f*s2/(n-&p)/n); output;
diff=xbar+sqrt(&p*(n-1)*f*s2/(n-&p)/n); output;
run;
/* The axis commands define the size of the plotting window.
* The horizontal axis is of the variables, and the vertical
* axis is used for the confidence limits.
* The reference line of 0 corresponds to the null value of the
* difference for each variable.
* /
proc gplot data=b;
axis1 length=4 in;
axis2 length=6 in;
plot diff*variable / vaxis=axis1 haxis=axis2 vref=0 lvref=21;
symbol v=none i=hilot color=black;
run;
(Which in this case is analogous to the earlier SAS program Download here: nutrient6.sas)
Profile plots for paired differences
To construct a profile plot with confidence limits:
1. Open the ‘spouse’ data set in a new worksheet.
2. Name the columns h1, h2, h3, h4, w1, w2, w3, and w4, from left to right.
3. Name new columns diff1, diff2, diff3, and diff4.
4. Calc > Calculator
a. Highlight and select 'diff1' to move it to the 'Store result' window.
b. In the Expression window, enter ‘h1’ - ‘w1’.
c. Choose 'OK'. The first difference is created in the worksheet.
5. Repeat step 4. for each of the other 3 differences.
6. Graph > Interval plot > Multiple Y variables with categorical variables > OK
a. Highlight and select all 4 difference variables (diff1 through diff4) to move them to the Y-variables window.
b. Display Y’s > Y’s first
c. Under Options, make sure the Mean confidence interval bar and Mean symbol are checked.
d. Choose 'OK', then 'OK' again. The profile plot is shown in the results area.
Analysis
Note: The plot is given in plot1 shown below:
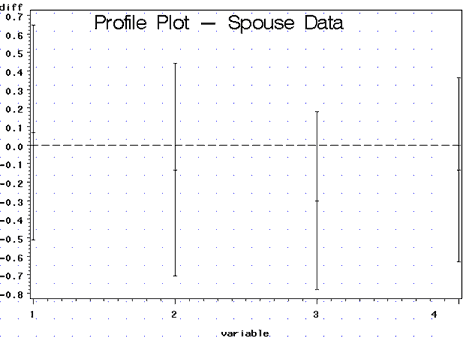
Here we can immediately notice that all of the simultaneous confidence intervals include 0 suggesting that the husbands and wives do not differ significantly in their responses to any of the questions. So what is going on here? Earlier Hotelling's \(T^{2}\) test told us that there was a significant difference between the husband and wives in their responses to the questions. But the plot of the confidence intervals suggests that there are no differences.
Basically, the significant Hotelling's T-square result is achieved through the contributions from all of the variables. It turns out that there is going to be a linear combination of the population means of the form:
\[\Psi = \sum_{j=1}^{p}c_j\mu_{Y_j}\]
whose confidence interval will not include zero.
The profile plot suggests that the largest difference occurs in response to question 3. Here, the wives respond more positively than their husbands to the question: "What is the level of companionate love you feel for your partner?"
7.1.11 - Question 2: Matching Perceptions
7.1.11 - Question 2: Matching PerceptionsExample 7-11: Spouse Data (Question 2)
Next, we will return to the second question posed earlier in this lesson.
Question 2: Do the husbands and wives accurately perceive the responses of their spouses?
To understand this question, let us return to the four questions asked of each husband and wife pair. The questions were:
- What is the level of passionate love you feel for your partner?
- What is the level of passionate love your partner feels for you?
- What is the level of companionate love you feel for your partner?
- What is the level of companionate love your partner feels for you?
Notice that these questions are all paired. The odd-numbered questions ask about how each person feels about their spouse, while the even-numbered questions ask how each person thinks their spouse feels towards them. The question that we are investigating now asks about perception, so here we are trying to see if the husbands accurately perceive the responses of their wives and conversely to the wives accurately perceive the responses of their husbands.
In more detail, we may ask:
In this case, we are asking if the wife accurately perceives the amount of passionate love her husband feels toward her.
Here, we are asking if the husband accurately perceives the amount of passionate love his wife feels toward him.
- Does the husband's answer to question 1 match the wife's answer to question 2?
- Secondly, does the wife's answer to question 1 match the husband's answer to question 2?
- Similarly, does the husband's answer to question 3 match the wife's answer to question 4?
- Does the wife's answer to question 3 match the husband's answer to question 4?
To address the research question we need to define four new variables as follows:
- \(Z_{i1} = X_{1i1} - X_{2i2}\) - (for the \(i^{th}\) couple, the husband's response to question 1 minus the wife's response to question 2.)
- \(Z_{i2} = X_{1i2} - X_{2i1}\) - (for the \(i^{th}\) couple, the husband's response to question 2 minus the wife's response to question 1.)
- \(Z_{i3} = X_{1i3} - X_{2i4}\) - (for the \(i^{th}\) couple, the husband's response to question 3 minus the wife's response to question 4.)
- \(Z_{i4} = X_{1i4} - X_{2i3}\) - (for the \(i^{th}\) couple, the husband's response to question 4 minus the wife's response to question 3.)
These Z's can then be collected into a vector. We can then calculate the sample mean for that vector...
\(\mathbf{\bar{z}} = \dfrac{1}{n}\sum_{i=1}^{n}\mathbf{Z}_i\)
as well as the sample variance-covariance matrix...
\(\mathbf{S}_Z = \dfrac{1}{n-1}\sum_{i=1}^{n}\mathbf{(Z_i-\bar{z})(Z_i-\bar{z})'}\)
Here we will make the usual assumptions about the vector \(Z_{i}\) containing the responses for the \(i^{th}\) couple:
- The \(Z_{i}\)'s have common mean vector \(\mu_{Z}\)
- The \(Z_{i}\)'s have common variance-covariance matrix \(\Sigma_{Z}\)
- Independence. The \(Z_{i}\)'s are independently sampled.
- Multivariate Normality. The \(Z_{i}\)'s are multivariate normally distributed.
Question 2 is equivalent to testing the null hypothesis that the mean \(\mu_{Z}\) is equal to 0, against the alternative that \(\mu_{Z}\) is not equal to 0 as expressed below:
\(H_0\colon \boldsymbol{\mu}_Z = \mathbf{0}\) against \(H_a\colon \boldsymbol{\mu}_Z \ne \mathbf{0}\)
We may then carry out the Paired Hotelling's T-Square test using the usual formula with the sample mean vector z-bar replacing the mean vector y-bar from our previous example, and the sample variance-covariance matrix \(S_{Z}\) replacing the sample variance-covariance matrix \(S_{Y}\) also from our previous example:
\(n\mathbf{\bar{z}'S^{-1}_Z\bar{z}}\)
We can then form the F-statistic as before:
\(F = \frac{n-p}{p(n-1)}T^2 \sim F_{p, n-p}\)
And, under \(H_{o} \colon \mu_{Z} = 0\) we will reject the null hypothesis \(H_{o}\) at level \(\alpha\) if this F-statistic exceeds the critical value from the F-table with p and n-p degrees of freedom evaluated at \(α\).
\(F > F_{p, n-p, \alpha}\)
The analysis may be carried out using the SAS program as shown below:
The SAS program hopefully resembles the program spouse.sas used to address question #1.
Download the SAS Program: spouse2.sas
Explore the code below to see how to find Hotelling's \(T^{2}\) using the SAS statistical software application.Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Paired Hotelling's T-Square: Matching Perceptions";
/* The differences 'd1' through 'd4' are defined
* and added to the data set.
*/
data spouse;
infile "D:\Statistics\STAT 505\data\spouse.csv" firstobs=2 delimiter=','
input h1 h2 h3 h4 w1 w2 w3 w4;
d1=h1-w2;
d2=h2-w1;
d3=h3-w4;
d4=h4-w3;
run;
proc print data=spouse;
run;
/* The iml code below defines and executes the 'hotel' module
* for calculating the one-sample Hotelling T2 test statistic.
* The calculations are based on the differences, which is why
* there is a single null vector consisting of only 0s.
* The commands between 'start' and 'finish' define the
* calculations of the module for an input vector 'x'.
* The 'use' statement makes the 'spouse' data set available, from
* which the difference variables are taken. The difference variables
* are then read into the vector 'x' before the 'hotel' module is called.
*/
proc iml;
start hotel;
mu0={0, 0, 0, 0};
one=j(nrow(x),1,1);
ident=i(nrow(x));
ybar=x`*one/nrow(x);
s=x`*(ident-one*one`/nrow(x))*x/(nrow(x)-1.0);
print mu0 ybar;
print s;
t2=nrow(x)*(ybar-mu0)`*inv(s)*(ybar-mu0);
f=(nrow(x)-ncol(x))*t2/ncol(x)/(nrow(x)-1);
df1=ncol(x);
df2=nrow(x)-ncol(x);
p=1-probf(f,df1,df2);
print t2 f df1 df2 p;
finish;
use spouse;
read all var{d1 d2 d3 d4} into x;
run hotel;
The output contains on its first page a printing of the data for each of the matrixes, including the transformations d1 through d4.
Page two contains the output from the iml procedure which carries out the Hotelling's \(T^{2}\) test. Again, we can see that \(\mu_{0}\) is defined to be a vector of 0's. The sample mean vectors are given under YBAR.
S is our sample variance-covariance matrix for the Z's.
Hotelling's T2 test for matched perceptions
To calculate the Hotelling T2 statistic for matched perceptions:
- Open the ‘spouse’ data set in a new worksheet.
- Name the columns h1, h2, h3, h4, w1, w2, w3, and w4, from left to right.
- Name new columns diff1, diff2, diff3, and diff4.
- Calc > Calculator
- Highlight and select 'diff1' to move it to the Store result window.
- In the Expression window, enter ‘h1’ - ‘w2’.
- Choose 'OK'. The first difference is created in the worksheet.
- Calc > Calculator
- Highlight and select 'diff2' to move it to the 'Store result' window.
- In the Expression window, enter ‘h2’ - ‘w1’.
- Choose 'OK'. The second difference is created in the worksheet.
- Calc > Calculator
- Highlight and select 'diff3' to move it to the 'Store result' window.
- In the Expression window, enter ‘h3’ - ‘w4’.
- Choose 'OK'. The third difference is created in the worksheet.
- Calc > Calculator
- Highlight and select 'diff2' to move it to the 'Store result' window.
- In the Expression window, enter ‘h4’ - ‘w3’.
- Choose 'OK'. The fourth difference is created in the worksheet.
- Stat > Basic Statistics > Store Descriptive Statistics
- Highlight and select all 4 difference variables (diff1 through diff4) to move them to the 'Variables' window.
- Under Statistics, choose ‘Mean’, and then ‘OK’.
- Choose ‘OK’ again. The 4 difference means are displayed in new columns in the worksheet.
- Data > Transpose Columns
- Highlight and select the 4 column names with the means from the step above.
- Choose ‘After last column in use’ then ‘OK'. The means are displayed in a single column in the worksheet.
- Name the new column of the numeric means ‘means’ for the remaining steps.
- Data > Copy > Columns to Matrix
- Highlight and select ‘means’ for the 'Copy from columns' window.
- Enter the ‘M1’ in the In current worksheet window. Then choose ‘OK’.
- Calc > Matrices > Transpose
- Highlight and select ‘M1’ in the 'Transpose from' window and enter ‘M2’ in the 'Store result' window.
- Choose ‘OK’.
- Stat > Basic Statistics > Covariance
- Highlight and select all 4 difference variables (diff1 through diff4) to move them to the Variables window.
- Check the box to 'Store matrix' and then choose ‘OK’. This will store the covariance matrix in a new variable ‘M3’.
- Calc > Matrices > Invert
- Highlight and select ‘M3’ to move it to the 'Invert from' window.
- Enter ‘M4’ in the 'Store result in' window and choose ‘OK’. This will store the inverted covariance matrix in a new variable ‘M4’.
- Calc > Matrices > Arithmetic
- Choose Multiply and enter M2 and M4, respectively in the two windows.
- Enter ‘M5’ as the name in the Store result window and then ‘OK’.
- Calc > Matrices > Arithmetic
- Choose Multiply and enter M5 and M1, respectively in the two windows.
- Enter ‘M6’ as the name in the Store result window and then ‘OK’. The answer 0.2143 is displayed in the results window.
- Calc > Calculator
- Enter C16 (or any unused column name) in the 'Store result' window.
- In the Expression window, enter 0.2143 * 30 (this is the answer from 16b times the sample size). Choose ‘OK’. The value of the T2 statistic 6.43 is displayed in the worksheet under ‘C16’.
Analysis
The Hotelling's \(T^{2}\) statistic comes out to be 6.43 approximately with a corresponding F of 1.44, with 4 and 26 degrees of freedom. The p-value is 0.24 which exceeds 0.05, therefore we do not reject the null hypothesis at the 0.05 level.
Conclusion
In conclusion, we can state that there is no statistically significant evidence against the hypothesis that husbands and wives accurately perceive the attitudes of their spouses. Our evidence includes the following statistics: ( \(T^{2}\) = 6.43; F = 1.44; d.f. = 4, 26; p = 0.249).
7.1.12 - Two-Sample Hotelling's T-Square
7.1.12 - Two-Sample Hotelling's T-SquareIntroduction
This test is the multivariate analog of the two-sample t-test in univariate statistics. These two sample tests, in both cases, are used to compare two populations. Two populations may correspond to two different treatments within an experiment.
For example, in a completely randomized design, the two treatments are randomly assigned to the experimental units. Here, we would like to distinguish between the two treatments. Another situation occurs where the observations are taken from two distinct populations. In either case, there is no pairing of the observations.
Example 7-12: Swiss Bank Notes

An example where we are sampling from two distinct populations occurs with 1000 franc Swiss Bank Notes.
- The first population is the population of Genuine Bank Notes
- The second population is the population of Counterfeit Bank Notes
While the diagram shows a more recent version issue of the 1000 franc note, it depicts the different measurement locations taken in this study. For both populations of banknotes the following measurements were taken:
- Length of the note
- Width of the Left-Hand side of the note
- Width of the Right-Hand side of the note
- Width of the Bottom Margin
- Width of the Top Margin
- Diagonal Length of Printed Area
Objective: To determine if counterfeit notes can be distinguished from genuine Swiss banknotes.
This is essential for the police if they wish to use these kinds of measurements to determine if a banknote is genuine or not and help solve counterfeiting crimes.
Before considering the multivariate case, we will first consider the univariate case...
7.1.13 - The Univariate Case
7.1.13 - The Univariate CaseSuppose we have data from a single variable from two populations:
- The data will be denoted in Population 1 as: \(X_{11}\),\(X_{12}\), ... , \(X_{1n_{1}}\)
- The data will be denoted in Population 2 as: \(X_{21}\), \(X_{22}\), ... , \(X_{2n_{2}}\)
For both populations, the first subscript will denote which population the note is from. The second subscript will denote which observation we are looking at from each population.
Here we will make the standard assumptions:
- The data from population i is sampled from a population with mean \(\mu_{i}\). This assumption simply means that there are no sub-populations to note.
- Homoskedasticity: The data from both populations have common variance \(σ^{2}\)
- Independence: The subjects from both populations are independently sampled.
- Normality: The data from both populations are normally distributed.
Here we are going to consider testing, \(H_0\colon \mu_1 = \mu_2\) against \(H_a\colon \mu_1 \ne \mu_2\), that the populations have equal means, against the alternative hypothesis that the means are not equal.
We shall define the sample means for each population using the following expression:
\(\bar{x}_i = \dfrac{1}{n_i}\sum_{j=1}^{n_i}X_{ij}\)
We will let \(s^2_i\) denote the sample variance for the \(i^{th}\) population, again calculating this using the usual formula below:
\(s^2_i = \dfrac{\sum_{j=1}^{n_i}X^2_{ij}-(\sum_{j=1}^{n_i}X_{ij})^2/n_i}{n_i-1}\)
Assuming homoskedasticity, both of these sample variances, \(s^2_1\) and \(s^2_2\), are estimates of the common variance \(σ^{2}\). A better estimate can be obtained, however, by pooling these two different estimates yielding the pooled variance as given in the expression below:
\(s^2_p = \dfrac{(n_1-1)s^2_1+(n_2-1)s^2_2}{n_1+n_2-2}\)
Our test statistic is the students' t-statistic which is calculated by dividing the difference in the sample means by the standard error of that difference. Here the standard error of that difference is given by the square root of the pooled variance times the sum of the inverses of the sample sizes as shown below:
\(t = \dfrac{\bar{x}_1-\bar{x}_2}{\sqrt{s^2_p(\dfrac{1}{n_1}+\frac{1}{n_2})}} \sim t_{n_1+n_2-2}\)
Under the null hypothesis, \(H_{o} \)of the equality of the population means, this test statistic will be t-distributed with \(n_{1}\) + \(n_{2}\) - 2 degrees of freedom.
We will reject \(H_{o}\) at level \(α\) if the absolute value of this test statistic exceeds the critical value from the t-table with \(n_{1}\) + \(n_{2}\) - 2 degrees of freedom evaluated at \(α/2\).
\(|t| > t_{n_1+n_2-2, \alpha/2}\)
All of this should be familiar to you from your introductory statistics course.
Next, let's consider the multivariate case...
7.1.14 - The Multivariate Case
7.1.14 - The Multivariate CaseIn this case we are replacing the random variables \(X_{ij}\), for the \(j_{th}\) sample for the \(i_{th}\) population, with random vectors \(X_{ij}\), for the \(j_{th}\) sample for the \(i_{th}\) population. These vectors contain the observations from the p variables.
In our notation, we will have our two populations:
- The data will be denoted in Population 1 as: \(X_{11}\),\(X_{12}\), ... , \(X_{1n_{1}}\)
- The data will be denoted in Population 2 as: \(X_{21}\), \(X_{22}\), ... , \(X_{2n_{2}}\)
Here the vector \(X_{ij}\) represents all of the data for all of the variables for sample unit j, for population i.
\(\mathbf{X}_{ij} = \left(\begin{array}{c}X_{ij1}\\X_{ij2}\\\vdots\\X_{ijp}\end{array}\right)\)
This vector contains elements \(X_{ijk}\) where k runs from 1 to p, for p different observed variables. So, \(X_{ijk}\) is the observation for variable k of subject j from population i.
The assumptions here will be analogous to the assumptions in the univariate setting.
Assumptions
- The data from population i is sampled from a population with mean vector \(\mu_{i}\). Again, this corresponds to the assumption that there are no sub-populations.
- Instead of assuming Homoskedasticity, we now assume that the data from both populations have a common variance-covariance matrix \(Σ\).
- Independence. The subjects from both populations are independently sampled.
- Normality. Both populations are normally distributed.
Consider testing the null hypothesis that the two populations have an identical population mean vectors. This is represented below as well as the general alternative that the mean vectors are not equal.
\(H_0: \boldsymbol{\mu_1 = \mu_2}\) against \(\boldsymbol{\mu_1 \ne \mu_2}\)
So here what we are testing is:
\(H_0\colon \left(\begin{array}{c}\mu_{11}\\\mu_{12}\\\vdots\\\mu_{1p}\end{array}\right) = \left(\begin{array}{c}\mu_{21}\\\mu_{22}\\\vdots\\\mu_{2p}\end{array}\right)\) against \(H_a\colon \left(\begin{array}{c}\mu_{11}\\\mu_{12}\\\vdots\\\mu_{1p}\end{array}\right) \ne \left(\begin{array}{c}\mu_{21}\\\mu_{22}\\\vdots\\\mu_{2p}\end{array}\right)\)
Or, in other words...
\(H_0\colon \mu_{11}=\mu_{21}\) and \(\mu_{12}=\mu_{22}\) and \(\dots\) and \(\mu_{1p}=\mu_{2p}\)
The null hypothesis is satisfied if and only if the population means are identical for all of the variables.
The alternative is that at least one pair of these means is different. This is expressed below:
\(H_a\colon \mu_{1k}\ne \mu_{2k}\) for at least one \( k \in \{1,2,\dots, p\}\)
To carry out the test, for each population i, we will define the sample mean vectors, calculated the same way as before, using data only from the\(i_{th}\) population.
\(\mathbf{\bar{x}}_i = \dfrac{1}{n_i}\sum_{j=1}^{n_i}\mathbf{X}_{ij}\)
Similarly, using data only from the \(i^{th}\) population, we will define the sample variance-covariance matrices:
\(\mathbf{S}_i = \dfrac{1}{n_i-1}\sum_{j=1}^{n_i}\mathbf{(X_{ij}-\bar{x}_i)(X_{ij}-\bar{x}_i)'}\)
Under our assumption of homogeneous variance-covariance matrices, both \(S_{1}\) and \(S_{2}\) are estimators for the common variance-covariance matrix Σ. A better estimate can be obtained by pooling the two estimates using the expression below:
\(\mathbf{S}_p = \dfrac{(n_1-1)\mathbf{S}_1+(n_2-1)\mathbf{S}_2}{n_1+n_2-2}\)
Again, each sample variance-covariance matrix is weighted by the sample size minus 1.
7.1.15 - The Two-Sample Hotelling's T-Square Test Statistic
7.1.15 - The Two-Sample Hotelling's T-Square Test StatisticNow we are ready to define the Two-sample Hotelling's T-Square test statistic. As in the expression below, you will note that it involves the computation of differences in the sample mean vectors. It also involves a calculation of the pooled variance-covariance matrix multiplied by the sum of the inverses of the sample size. The resulting matrix is then inverted.
\(T^2 = \mathbf{(\bar{x}_1 - \bar{x}_2)}^T\{\mathbf{S}_p(\frac{1}{n_1}+\frac{1}{n_2})\}^{-1} \mathbf{(\bar{x}_1 - \bar{x}_2)}\)
For large samples, this test statistic will be approximately chi-square distributed with \(p\) degrees of freedom. However, as before this approximation does not take into account the variation due to estimating the variance-covariance matrix. So, as before, we will look at transforming this Hotelling's T-square statistic into an F-statistic using the following expression.
Note! This is a function of the sample sizes of the two populations and the number of variables measured p.
\(F = \dfrac{n_1+n_2-p-1}{p(n_1+n_2-2)}T^2 \sim F_{p, n_1+n_2-p-1}\)
Under the null hypothesis, \(H_{o}\colon \mu_{1} = \mu_{2}\) this F-statistic will be F-distributed with p and \(n_{1} + n_{2} - p\) degrees of freedom. We would reject \(H_{o}\) at level \(α\) if it exceeds the critical value from the F-table evaluated at \(α\).
\(F > F_{p, n_1+n_2-p-1, \alpha}\)
Example 7-13: Swiss Banknotes (Two-Sample Hotelling's)
The two-sample Hotelling's \(T^{2}\) test can be carried out using the Swiss Banknotes data using the SAS program as shown below:
Data file: swiss3.csv
Download the SAS Program: swiss10.sas
Download the output: swiss10.lst.
Explore the code below to see how to compute the Two Sample Hotelling's \(T^2\) using the SAS statistical software application.
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "2-Sample Hotellings T2 - Swiss Bank Notes";
data swiss;
infile "D:\Statistics\STAT 505\data\swiss3.csv" firstobs=2 delimiter=','
input type $ length left right bottom top diag;
run;
/* The iml code below defines and executes the 'hotel2' module
* for calculating the two-sample Hotelling T2 test statistic.
* The commands between 'start' and 'finish' define the
* calculations of the module for two input vectors 'x1' and 'x2',
* which have the same variables but correspond to two separate groups.
* The 'use' statement makes the 'swiss' data set available, from
* which all the variables are taken. The variables are then read
* separately into the vectors 'x1' and 'x2' for each group, and
* finally the 'hotel2' module is called.
*/
proc iml;
start hotel2;
n1=nrow(x1);
n2=nrow(x2);
k=ncol(x1);
one1=j(n1,1,1);
one2=j(n2,1,1);
ident1=i(n1);
ident2=i(n2);
ybar1=x1`*one1/n1;
s1=x1`*(ident1-one1*one1`/n1)*x1/(n1-1.0);
print n1 ybar1;
print s1;
ybar2=x2`*one2/n2;
s2=x2`*(ident2-one2*one2`/n2)*x2/(n2-1.0);
print n2 ybar2;
print s2;
spool=((n1-1.0)*s1+(n2-1.0)*s2)/(n1+n2-2.0);
print spool;
t2=(ybar1-ybar2)`*inv(spool*(1/n1+1/n2))*(ybar1-ybar2);
f=(n1+n2-k-1)*t2/k/(n1+n2-2);
df1=k;
df2=n1+n2-k-1;
p=1-probf(f,df1,df2);
print t2 f df1 df2 p;
finish;
use swiss;
read all var{length left right bottom top diag} where (type="real") into x1;
read all var{length left right bottom top diag} where (type="fake") into x2;
run hotel2;
At the top of the first output page, you see that N1 is equal to 100 indicating that we have 100 banknotes in the first sample. In this case 100 real or genuine notes.
Computing the 2-sample Hotelling's T2
To compute the two-sample (pooled variance) Hotelling’s T2 statistic:
- Open the ‘swiss3’ data set in a new worksheet.
- Rename the columns type, length, left, right, bottom, top, and diag.
- Stat > ANOVA > General MANOVA
- Highlight and select all six response variables (length through diag) to move them to the Responses window.
- Highlight and select 'type' to move it to the Model window.
- Choose 'OK'. The corresponding F-statistic 391.92 is shown in the results area.
- To calculate the specific value of the T2 statistic:
- Name new columns in the worksheet p, n1, n2, and F, and enter the values corresponding to this example: 6, 100, 100, and 391.92 in their row.
- Calc > Calculator
- Enter C12 (or any new column name) for the 'Store result' window.
- In the Expression window, enter ‘p’ * (‘n1’ + ‘n2’ - 2) * ‘F’ / (‘n1’ + ‘n2’ - ‘p’ - 1).
- Choose 'OK'. The T2 value 2412.44 is reported in the new worksheet column.
Analysis
The sample mean vectors are copied into the table below:
| Means | ||
|---|---|---|
| Variable | Genuine | Counterfeit |
| Length | 214.969 | 214.823 |
| Left Width | 129.943 | 130.300 |
| Right Width | 129.720 | 130.193 |
| Bottom Margin | 8.305 | 10.530 |
| Top Margin | 10.168 | 11.133 |
| Diagonal | 141.517 | 139.450 |
The sample variance-covariance matrix for the real or genuine notes appears below:
\(S_1 = \left(\begin{array}{rrrrrr}0.150& 0.058& 0.057 &0.057&0.014&0.005\\0.058&0.133&0.086&0.057&0.049&-0.043\\0.057&0.086&0.126&0.058&0.031&-0.024\\0.057&0.057&0.058&0.413&-0.263&-0.000\\0.014&0.049&0.031&-0.263&0.421&-0.075\\0.005&-0.043&-0.024&-0.000&-0.075&0.200\end{array}\right)\)
The sample variance-covariance for the second sample of notes, the counterfeit note, is given below:
\(S_2 = \left(\begin{array}{rrrrrr}0.124&0.032&0.024&-0.101&0.019&0.012\\0.032&0.065&0.047&-0.024&-0.012&-0.005\\0.024&0.047&0.089&-0.019&0.000&0.034\\-0.101&-0.024&-0.019&1.281&-0.490&0.238\\ 0.019&-0.012&0.000&-0.490&0.404&-0.022\\0.012&-0.005&0.034&0.238&-0.022&0.311\end{array}\right)\)
This is followed by the pooled variance-covariance matrix for the two samples.
\(S_p = \left(\begin{array}{rrrrrr}0.137&0.045&0.041&-0.022&0.017&0.009\\0.045&0.099&0.066&0.016&0.019&-0.024\\0.041&0.066&0.108&0.020&0.015&0.005\\-0.022&0.016&0.020&0.847&-0.377&0.119\\0.017&0.019&0.015&-0.377&0.413&-0.049\\0.009&-0.024&0.005&0.119&-0.049&0.256\end{array}\right)\)
The two-sample Hotelling's \(T^{2}\) statistic is 2412.45. The F-value is about 391.92 with 6 and 193 degrees of freedom. The p-value is close to 0 and so we will write this as \(< 0.0001\).
In this case, we can reject the null hypothesis that the mean vector for the counterfeit notes equals the mean vector for the genuine notes given the evidence as usual: (\(T_{2} = 2412.45\); \(F = 391.92\); \(d. f. = 6, 193\); \(p< 0.0001\))
Conclusion
The counterfeit notes can be distinguished from the genuine notes on at least one of the measurements.
After concluding that the counterfeit notes can be distinguished from the genuine notes the next step in our analysis is to determine upon which variables they are different.
7.1.16 - Summary of Basic Material
7.1.16 - Summary of Basic MaterialIn this section we discussed:
- Application of Hotelling's T-square statistics to carry out inferences on a single-sample mean, paired sample means, and two-sample means
- How to set up a confidence interval for a population mean vector
- What is a profile plot and how to draw it
A more in-depth analysis of some of these topics is done in the Advanced section.
7.2 - Advanced
7.2 - AdvancedIn this section, we touch upon some of the intricate details of inference for a multivariate population mean. The reader should be aware of these issues.
7.2.1 - Profile Analysis for One Sample Hotelling's T-Square
7.2.1 - Profile Analysis for One Sample Hotelling's T-SquareLet us revisit the original hypothesis of interest, as below
\(H_0\colon \boldsymbol{\mu} = \boldsymbol{\mu_0}\) against \(H_a\colon \boldsymbol{\mu} \ne \boldsymbol{\mu_a}\)
Note! It is equivalent to testing this null hypothesis:
\(H_0\colon \dfrac{\mu_1}{\mu^0_1} = \dfrac{\mu_2}{\mu^0_2} = \dots = \dfrac{\mu_p}{\mu^0_p} = 1\)
against the alternative that at least one of these ratios is not equal to 1, (below):
\(H_a\colon \dfrac{\mu_j}{\mu^0_j} \ne 1\) for at least one \(j \in \{1,2,\dots, p\}\)
Instead of testing the null hypothesis for the ratios of the means over their hypothesized means are all equal to one, profile analysis involves testing the null hypothesis that all of these ratios are equal to one another, but not necessarily equal to 1.
After rejecting
\(H_0\colon \dfrac{\mu_1}{\mu^0_1} = \dfrac{\mu_2}{\mu^0_2} = \dots = \dfrac{\mu_p}{\mu^0_p} = 1\)
we may wish to test
\(H_0\colon \dfrac{\mu_1}{\mu^0_1} = \dfrac{\mu_2}{\mu^0_2} = \dots = \dfrac{\mu_p}{\mu^0_p}\)
Profile Analysis can be carried out using the following procedure.
Step 1: Compute the differences between the successive ratios. That is we take the ratio of the j + 1-th variable over its hypothesized mean and subtract this from the ratio of jth variable over its hypothesized mean as shown below:
\(D_{ij} = \dfrac{X_{ij+1}}{\mu^0_{j+1}}-\dfrac{X_{ij}}{\mu^0_j}\)
We call this ratio \(D_{ij}\) for observation i.
Note! That, testing the null hypothesis that all of the ratios are equal to one another
\(H_0\colon \dfrac{\mu_1}{\mu^0_1} = \dfrac{\mu_2}{\mu^0_2} = \dots = \dfrac{\mu_p}{\mu^0_p}\)
is equivalent to testing the null hypothesis that all the mean differences are going to be equal to 0.
\(H_0\colon \boldsymbol{\mu}_D = \mathbf{0}\)
Step 2: Apply Hotelling’s \(T^{2}\) test to the data \(D_{ij}\) to test the null hypothesis that the mean of these differences is equal to 0.
\(H_0\colon \boldsymbol{\mu}_D = \mathbf{0}\)
This is carried out using the SAS program as shown below:
download the SAS Program here: nutrient8.sas
Explore the code for an explanation of the SAS code.Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Profile Analysis - Women's Nutrition Data";
/* After reading in the data, each of the original
* variables is divided by its null value to convert
* to a common scale without specific units.
* The differences are then defined for each successive
* pair of variables.
*/
data nutrient;
infile "D:\Statistics\STAT 505\data\nutrient.csv" firstobs=2 delimiter=','
input id calcium iron protein a c;
calcium=calcium/1000;
iron=iron/15;
protein=protein/60;
a=a/800;
c=c/75;
diff1=iron-calcium;
diff2=protein-iron;
diff3=a-protein;
diff4=c-a;
run;
/* The iml code to compute the hotelling t2 statistic
* is similar to that for the one-sample t2 statistic
* except that by working with differences of variable,
* the null values are all 0s, and the corresponding
* null hypothesis is that all variable means are equal
* to each other.
*/
proc iml;
start hotel;
mu0={0,0,0,0};
one=j(nrow(x),1,1);
ident=i(nrow(x));
ybar=x`*one/nrow(x);
s=x`*(ident-one*one`/nrow(x))*x/(nrow(x)-1.0);
print mu0 ybar;
print s;
t2=nrow(x)*(ybar-mu0)`*inv(s)*(ybar-mu0);
f=(nrow(x)-ncol(x))*t2/ncol(x)/(nrow(x)-1);
df1=ncol(x);
df2=nrow(x)-ncol(x);
p=1-probf(f,df1,df2);
print t2 f df1 df2 p;
finish;
use nutrient;
read all var{diff1 diff2 diff3 diff4} into x;
run hotel;
Profile analysis
To test the hypothesis of equal mean ratios:
- Open the ‘nutrient’ data set in a new worksheet.
- Name the columns id, calcium, iron, protein, vit_A, and vit_C, from left to right.
- Name new columns diff1, diff2, diff3, and diff4.
- Calc > Calculator
- Highlight and select 'diff1' to move it to the 'Store result' window.
- In the Expression window, enter ‘iron’ / 15 - ‘calcium’ / 1000, where the values 15 and 1000 come from the null values of interest for iron and calcium, respectively.
- Choose 'OK'. The difference between the iron and calcium ratios is displayed in the worksheet variable diff1.
- Calc > Calculator
- Highlight and select 'diff2' to move it to the Store result window.
- In the Expression window, enter ‘protein’ / 60 - ‘iron’ / 15, where the values 60 and 15 come from the null values of interest for protein and iron, respectively.
- Choose 'OK'. The difference between the protein and iron ratios is displayed in the worksheet variable diff2.
- Repeat step 5. for the difference between the vitamin A ratio and the protein ratio, where each ratio is obtained by dividing the original variable by its null value.
- Repeat step 5. again for the last difference, which is between the vitamin C ratio and the vitamin A ratio.
- Stat > Basic Statistics > Store Descriptive Statistics
- Highlight and select all 4 difference variables (diff1 through diff4) to move them to the 'Variables' window.
- Under Statistics, choose ‘Mean’, and then ‘OK’.
- Choose ‘OK’ again. The 4 difference means are displayed in five new columns in the worksheet.
- Data > Transpose Columns
- Highlight and select the 4 column names with the means from the step above.
- Choose ‘After last column in use’ then ‘OK'. The means are displayed in a single column in the worksheet.
- Name the new column of the numeric means ‘means’ for the remaining steps.
- Data > Copy > Columns to Matrix
- Highlight and select ‘means’ for the 'Copy from columns' window.
- Enter the ‘M1’ in the In current worksheet window. Then choose ‘OK’.
- Calc > Matrices > Transpose
- Highlight and select ‘M1’ in the 'Transpose from' window and enter ‘M2’ in the 'Store result' window.
- Choose ‘OK’.
- Stat > Basic Statistics > Covariance
- Highlight and select all 4 difference variables (diff1 through diff4) to move them to the 'Variables' window.
- Check the box to Store matrix and then choose ‘OK’. This will store the covariance matrix in a new variable ‘M3’.
- Calc > Matrices > Invert
- Highlight and select ‘M3’ to move it to the 'Invert from' window.
- Enter ‘M4’ in the 'Store result in' window and choose ‘OK’. This will store the inverted covariance matrix in a new variable ‘M4’.
- Calc > Matrices > Arithmetic
- Choose Multiply and enter M2 and M4, respectively in the two windows.
- Enter ‘M5’ as the name in the 'Store result' window and then ‘OK’.
- Calc > Matrices > Arithmetic
- Choose Multiply and enter M5 and M1, respectively in the two windows.
- Enter ‘M6’ as the name in the 'Store result' window and then ‘OK’. The answer 1.39864 is displayed in the results window.
- Calc > Calculator
- Enter C16 (or any unused column name) in the 'Store result' window.
- In the Expression window, enter 1.39864 * 737 (this is the answer from 16b times the sample size). Choose ‘OK’. The value of the T2 statistic is displayed in the worksheet under ‘C16’.
Analysis
The results yield a Hotelling's \(T^{2}\) of 1,030.7953 and an F value of 256.64843, 4, and 733 degrees of freedom, and a p-value very close to 0.
| MU0 | YBAR |
|---|---|
| 0 | 0.1179441 |
| 0 | 0.3547307 |
| 0 | -0.04718 |
| 0 | 0.0028351 |
| S | ||||
|---|---|---|---|---|
| 0.191621 | -0.071018 | 0.0451147 | -0.037562 | |
| -0.071018 | 0.1653837 | -0.178844 | 0.029556 | |
| 0.0451147 | -0.178844 | 4.123726 | -3.755071 | |
| -0.037562 | 0.029556 | -3.75507 | -3.755071 | |
| T2 | F | DF1 | DF2 | P |
|---|---|---|---|---|
| 1030.7953 | 256.64843 | 4 | 733 | 0 |
Example 7-14: Women’s Health Survey
Here we can reject the null hypothesis that the ratio of mean intake over the recommended intake is the same for each nutrient as the evidence has shown here:
\( T ^ { 2 } = 1030.80 ; F = 256.65 ; \mathrm { d.f. } = 4,733 ; p < 0.0001 \)
This null hypothesis could be true if, for example, all the women were taking in nutrients in their required ratios, but they were either eating too little or eating too much.
7.2.2 - Upon Which Variable do the Swiss Banknotes Differ? -- Two Sample Mean Problem
7.2.2 - Upon Which Variable do the Swiss Banknotes Differ? -- Two Sample Mean ProblemWhen the hypothesis of equality of two independent population means is rejected, one would like to know on account of which variable the hypothesis is rejected. To assess that, we go back to the example of Swiss Banknotes.
To assess which variable these notes differ on we will consider the \(( 1 - \alpha ) \times 100 \%\) Confidence Ellipse for the difference in the population mean vectors for the two populations of banknotes, \(\boldsymbol{\mu_{1}}\) - \(\boldsymbol{\mu_{2}}\). This ellipse is given by the set of \(\boldsymbol{\mu_{1}}\) satisfying the expression:
\(\mathbf{(\bar{x}_1-\bar{x}_2-(\pmb{\mu}_1-\pmb{\mu}_2))}'\left\{\mathbf{S}_p \left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right) \right\}^{-1}\mathbf{(\bar{x}_1-\bar{x}_2-(\pmb{\mu}_1-\pmb{\mu}_2))} \le \dfrac{p(n_1+n_2-2)}{n_1+n_2-p-1}F_{p,n_1+n_2-p-1,\alpha}\)
To understand the geometry of this ellipse, let
\(\lambda_1, \lambda_2, \dots, \lambda_p\)
denote the eigenvalues of the pooled variance-covariance matrix \(S_{p}\), and let
\(\mathbf{e}_{1}\), \(\mathbf{e}_{2}\), ..., \(\mathbf{e}_{p}\)
denote the corresponding eigenvectors. Then the \(k^{th}\) axis of this p dimensional ellipse points in the direction specified by the \(k^{th}\) eigenvector, \(\mathbf{e}_{k}\) And, it has a half-length given by the expression below:
\[l_k = \sqrt{\lambda_k\frac{p(n_1+n_2-2)}{n_1+n_2-p-1}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)F_{p,n_1+n_2-p-1,\alpha}}\]
Note, again, that this is a function of the number of variables, p, the sample sizes \(n_{1}\) and \(n_{2}\), and the critical value from the F-table.
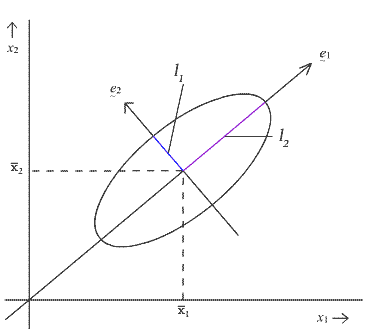
The \(( 1 - \alpha ) \times 100 \%\) confidence ellipse yields simultaneous \(( 1 - \alpha ) \times 100 \%\) confidence intervals for all linear combinations of the form given in the expression below:
\(c_1(\mu_{11}-\mu_{21})+c_2(\mu_{12}-\mu_{22})+\dots+c_p(\mu_{1p}-\mu_{2p}) = \sum_{k=1}^{p}c_k(\mu_{1k}-\mu_{2k}) = \mathbf{c'(\mu_1-\mu_k)}\)
So, these are all linear combinations of the differences in the sample means between the two populations where we are taking linear combinations across variables. These simultaneous confidence intervals are given by the expression below:
\(\sum_{k=1}^{p}c_k(\bar{x}_{1k}-\bar{x}_{2k}) \pm \sqrt{\dfrac{p(n_1+n_2-2)}{n_1+n_2-p-1}F_{p,n_1+n_2-p-1,\alpha}}\sqrt{\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right) \sum_{k=1}^{p}\sum_{l=1}^{p}c_kc_ls^{(p)}_{kl}}\)
Here, the terms \(s^{(p)}_{kl}\) denote the pooled covariances between variables k and l.
Interpretation
The interpretation of these confidence intervals is the same as that for the one sample of Hotelling's T-square. Here, we are \(( 1 - \alpha ) \times 100 \%\) confident that all of these intervals cover their respective linear combinations of the differences between the means of the two populations. In particular, we are also \(( 1 - \alpha ) \times 100 \%\) confident that all of the intervals of the individual variables also cover their respective differences between the population means. For the individual variables, if we are looking at, say, the \(k^{th}\) individual variable, then we have the difference between the sample means for that variable, k, plus or minus the same radical term that we had in the expression previously, times the standard error of that difference between the sample means for the \(k^{th}\) variable. The latter involves the inverses of the sample sizes and the pooled variance for variable k.
\(\bar{x}_{1k}-\bar{x}_{2k} \pm \sqrt{\dfrac{p(n_1+n_2-2)}{n_1+n_2-p-1}F_{p,n_1+n_2-p-1,\alpha}}\sqrt{\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right) s^2_k}\)
So, here, \(s^2_k\) is the pooled variance for variable k. These intervals are called simultaneous confidence intervals.
Let's work through an example of their calculation using the Swiss Banknotes data.
7.2.3 - Example: Swiss Banknotes
7.2.3 - Example: Swiss BanknotesExample 7-15: Swiss Banknotes
An example of the calculation of simultaneous confidence intervals using the Swiss Banknotes data is given in the expression below:
\(\bar{x}_{1k}-\bar{x}_{2k} \pm \sqrt{\frac{p(n_1+n_2-2)}{n_1+n_2-p-1}F_{p,n_1+n_2-p-1,\alpha}}\sqrt{\left(\frac{1}{n_1}+\frac{1}{n_2}\right) s^2_k}\)
Here we note that the sample sizes are both equal to 100, \(n = n_{1} = n_{2} =100\), so there is going to be a simplification of our formula inside the radicals as shown above.
Carrying out the math for the variable Length, we end up with an interval that runs from -0.044 to 0.336 as shown below.
The SAS program, below, can be used to compute the simultaneous confidence intervals for the 6 variables.
Download the SAS program here: swiss11.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Confidence Intervals - Swiss Bank Notes";
/* %let allows the p variable to be used throughout the code below
*/
%let p=6;
data swiss;
infile "D:\Statistics\STAT 505\data\swiss3.csv" firstobs=2 delimiter=','
input type $ length left right bottom top diag;
run;
/* A new data set named 'real' is created, consisting
* of only the real notes. This is used for calculation
* of the statistics needed for the last step.
* Also, where each variable is originally in its own column,
* these commands stack the data so that all variable names
* are in one column called 'variable', and all response values
* are in another column called 'x'.
*/
data real;
set swiss;
if type="real";
variable="length"; x=length; output;
variable="left"; x=left; output;
variable="right"; x=right; output;
variable="bottom"; x=bottom; output;
variable="top"; x=top; output;
variable="diagonal"; x=diag; output;
keep type variable x;
run;
proc sort;
by variable;
run;
/* The means procedure calculates and saves the sample size,
* mean, and variance for each variable. It then saves these results
* in a new data set 'pop1', corresponding to the real notes.
*/
proc means data=real noprint;
by variable;
id type;
var x;
output out=pop1 n=n1 mean=xbar1 var=s21;
/* A new data set named 'fake' is created, consisting
* of only the fake notes. This is used for calculation
* of the statistics needed for the last step.
* Also, where each variable is originally in its own column,
* these commands stack the data so that all variable names
* are in one column called 'variable', and all response values
* are in another column called 'x'.
*/
data fake;
set swiss;
if type="fake";
variable="length"; x=length; output;
variable="left"; x=left; output;
variable="right"; x=right; output;
variable="bottom"; x=bottom; output;
variable="top"; x=top; output;
variable="diagonal"; x=diag; output;
keep type variable x;
run;
proc sort;
by variable;
run;
/* The means procedure calculates and saves the sample size,
* mean, and variance for each variable. It then saves these results
* in a new data set 'pop2', corresponding to the fake notes.
*/
proc means data=fake noprint;
by variable;
id type;
var x;
output out=pop2 n=n2 mean=xbar2 var=s22;
/* This last step combines the two separate data sets to one
* and computes the 95% simultaneous confidence interval limits
* from the statistics calculated previously.
* The variances are pooled from both the real and the fake samples.
*/
data combine;
merge pop1 pop2;
by variable;
f=finv(0.95,&p,n1+n2-&p-1);
t=tinv(1-0.025/&p,n1+n2-2);
sp=((n1-1)*s21+(n2-1)*s22)/(n1+n2-2);
losim=xbar1-xbar2-sqrt(&p*(n1+n2-2)*f*(1/n1+1/n2)*sp/(n1+n2-&p-1));
upsim=xbar1-xbar2+sqrt(&p*(n1+n2-2)*f*(1/n1+1/n2)*sp/(n1+n2-&p-1));
lobon=xbar1-xbar2-t*sqrt((1/n1+1/n2)*sp);
upbon=xbar1-xbar2+t*sqrt((1/n1+1/n2)*sp);
run;
proc print data=combine;
run;
The downloadable results as listed here: swiss11.lst.
At this time Minitab does not support this procedure.
Analysis
| Obs | Variable | type | _TYPE | _FREQ_ | n1 | xbar1 | s21 | n2 | xbar1 | s22 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | bottom | fake | 0 | 100 | 100 | 8.305 | 0.41321 | 100 | 10.530 | 1.28131 |
| 2 | diagon | fake | 0 | 100 | 100 | 141.517 | 0.19981 | 100 | 139.450 | 0.31121 |
| 3 | left | fake | 0 | 100 | 100 | 129.943 | 0.13258 | 100 | 130.300 | 0.06505 |
| 4 | length | fake | 0 | 100 | 100 | 214.969 | 0.15024 | 100 | 214.823 | 0.12401 |
| 5 | right | fake | 0 | 100 | 100 | 129.720 | 0.12626 | 100 | 130.193 | 0.08894 |
| 6 | top | fake | 0 | 100 | 100 | 10.168 | 0.42119 | 100 | 11.133 | 0.40446 |
| Obs | f | t | sp | losim | upsim | lobon | upbon |
|---|---|---|---|---|---|---|---|
| 1 | 2.14580 | 2.66503 | 0.84726 | -2.69809 | 1.75191 | -2.57192 | -1.97808 |
| 2 | 2.14580 | 2.66503 | 0.2551 | 1.80720 | 2.32680 | 1.87649 | 2.25751 |
| 3 | 2.14580 | 2.66503 | 0.09881 | -0.51857 | -0.19543 | -0.47547 | -0.23853 |
| 4 | 2.14580 | 2.66503 | 0.13713 | -0.04433 | 0.33633 | 0.00643 | 0.28557 |
| 5 | 2.14580 | 2.66503 | 0.10760 | -0.64160 | -0.30440 | -0.59663 | -0.34937 |
| 6 | 2.14580 | 2.66503 |
0.41282 |
-1.29523 | -0.63477 | -1.20716 | -0.72284 |
The bounds of the simultaneous confidence intervals are given in columns for losim and upsim. Those entries are copied into the table below:
| Variable | 95% Confidence Interval |
|---|---|
| Length | -0.044, 0.336 |
| Left Width | -0.519, -0.195 |
| Right Width | -0.642, -0.304 |
| Bottom Margin | -2.698, -1.752 |
| Top Margin | -1.295, -0.635 |
| Diagonal | 1.807, 2.327 |
You need to be careful where they appear in the table in the output.
When interpreting these intervals we need to see which intervals include 0, which ones fall entirely below 0, and which ones fall entirely above 0.
The first thing that we notice is that interval for length includes 0. This suggests that we can not distinguish between the lengths of counterfeit and genuine banknotes. The intervals for both width measurements fall below 0.
Since these intervals are being calculated by taking the genuine notes minus the counterfeit notes this would suggest that the counterfeit notes are larger on these variables and we can conclude that the left and right margins of the counterfeit notes are wider than the genuine notes.
Similarly, we can conclude that the top and bottom margins of the counterfeit are also too large. Note, however, that the interval for the diagonal measurements falls entirely above 0. This suggests that the diagonal measurements of the counterfeit notes are smaller than that of the genuine notes.
Conclusions
- Counterfeit notes are too wide on both the left and right margins.
- The top and bottom margins of the counterfeit notes are too large.
- The diagonal measurement of the counterfeit notes is smaller than that of the genuine notes.
- Cannot distinguish between the lengths of counterfeit and genuine banknotes.
7.2.4 - Bonferroni Corrected (1 - α) x 100% Confidence Intervals
7.2.4 - Bonferroni Corrected (1 - α) x 100% Confidence IntervalsAs in the one-sample case, the simultaneous confidence intervals should be computed only when we are interested in linear combinations of the variables. If the only intervals of interest, however, are the confidence intervals for the individual variables with no linear combinations, then a better approach is to calculate the Bonferroni corrected confidence intervals as given in the expression below:
\(\bar{x}_{1k} - \bar{x}_{2k} \pm t_{n_1+n_2-2, \frac{\alpha}{2p}}\sqrt{s^2_k\left(\dfrac{1}{n_1}+\frac{1}{n_2}\right)}\)
Carrying out the math we end up with an interval that runs from 0.006 to 0.286 as shown below:
\(\bar{x}_{1k} - \bar{x}_{2k} \pm t_{2n-2, \frac{\alpha}{2p}}\sqrt{\frac{2s^2_k}{n}}\)
\(214.959 - 214.813 \pm \underset{2.665}{\underbrace{t_{2\times 100-2, \frac{0.05}{2 \times 6}}}}\sqrt{\dfrac{2 \times 0.137}{100}}\)
\((0.006, 0.286)\)
These calculations can also be obtained from the SAS program as shown below:
Download the SAS Program here: swiss11.sas
Looking at the data step combined and moving down, we can see that the fourth line sets t=tinv. This calculates the critical value from the t-table as desired. Then the lower and upper bounds for the Bonferroni intervals are calculated under lobon and upbon at the bottom of this data step.
The downloadable output is given here: swiss11.lst places the results in the columns for lobon and upbon.
Again, make sure you note that the variables are given in alphabetical order rather than in the original order of the data. In any case, you should be able to see where the numbers in the SAS output appear in the table below:
Computing the 2 sample Bonferroni CIs
To compute the two-sample Bonferroni CIs:
- Open the ‘swiss3’ data set in a new worksheet
- Rename the columns type, length, left, right, bottom, top, and diag.
- Calc > Basic Statistics > 2-sample t
- Choose ‘Both samples are in one column’ in the first window.
- Highlight and select length to move it to the Samples window.
- Highlight and select type to move it to the Sample IDs window.
- Under ‘Options’, enter 99.17, which corresponds to 1-0.05/6, the adjusted individual confidence level for simultaneous 95% confidence with the Bonferroni method.
- Check the box to Assume equal variances.
- Select Difference not equal for the Alternative hypothesis.
- Select ‘OK’ twice. The intervals for length are displayed in the results area.
- Repeat steps 3. and 4. for each of the other 5 variables. The six resulting intervals together may be interpreted with simultaneous 95% confidence.
Analysis
In summary, we have:
| Variable | 95% Simultaneous Confidence Intervals (Bonferroni corrected) |
|---|---|
| Length | 0.006, 0.286 |
| Left Width | -0.475, -0.239 |
| Right Width | -0.597, -0.349 |
| Bottom Margin | -2.572, -1.878 |
| Top Margin | -1.207, -0.723 |
| Diagonal | 1.876, 2.258 |
The intervals are interpreted in a way similar to before. Here we can see that:
Conclusions
- Length: Genuine notes are longer than counterfeit notes.
- Left-width and Right-width: Counterfeit notes are too wide on both the left and right margins.
- Top and Bottom margins: Counterfeit notes are too large.
- Diagonal measurement: The counterfeit notes are smaller than the genuine notes.
7.2.5 - Profile Plots
7.2.5 - Profile PlotsProfile plots provide another useful graphical summary of the data. These are only meaningful if all variables have the same units of measurement. They are not meaningful if the variables have different units of measurement. For example, some variables may be measured in grams while other variables are measured in centimeters. In this case, profile plots should not be constructed.
- In the traditional profile plot, the samples mean for each group is plotted against the variables.
- For the bank notes, it is preferable to subtract the government specifications before carrying out the analyses.
This plot can be obtained by the below:
Download the SAS Program here: swiss13b.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Profile Plot - Swiss Bank Notes";
/* After reading in the swiss data, where each variable is
* originally in its own column, the next statements stack the data
* so that all variable names are in one column called 'variable',
* and all response values minus their null values
* are in another column called 'x'.
* The subtraction is useful for plotting purposes because
* it allows for a common reference value of 0 for all variables.
*/
data swiss;
infile "D:\Statistics\STAT 505\data\swiss3.csv" firstobs=2 delimeter=',';
input type $ length left right bottom top diag;
variable="length"; x=length-215.0; output;
variable="left "; x=left-130.0; output;
variable="right "; x=right-130.0; output;
variable="bottom"; x=bottom-9.0; output;
variable="top "; x=top-10.0; output;
variable="diag "; x=diag-141.354; output;
run;
proc sort;
by type variable;
run;
/* The means procedure calculates and saves mean for
* each variable and saves the results in a new data set 'a'
* for use in the steps below.
* /
proc means data=swiss;
by type variable;
var x;
output out=a mean=xbar;
run;
/* The axis commands define the size of the plotting window.
* The horizontal axis is of the variables, and the vertical
* axis is used for the mean values.
* /
proc gplot;
axis1 length=4 in label=("Mean");
axis2 length=6 in;
plot xbar*variable=type / vaxis=axis1 haxis=axis2;
symbol1 v=J f=special h=2 i=join color=black;
symbol2 v=K f=special h=2 i=join color=black;
run;
2 sample profile plot
To compute the two-sample profile plot:
- Open the ‘swiss3’ data set in a new worksheet
- Rename the columns type, length, left, right, bottom, top, and diag.
- Name six new columns in the worksheet: length2 through diag2.
- Calc > Calculator
- Highlight and select length2 to move it to the Store result window.
- In the Expression window, enter ‘length’ - 215, where the value 215 comes from the null value of interest (government specification) for length.
- Choose 'OK'. The length2 variable is populated in the worksheet.
- Repeat step 4. for the other five variables, dividing each by its null value of interest.
- Graph > Line plot > Multiple Y’s with groups > OK
- Highlight and select all 6 variables created in steps 4 and 5 (length2 through diag2) to move them to the Y-variables window.
- Choose type for the Group variable.
- Display Y’s > Y’s first
- Under Options, make sure the Mean confidence interval bar and Mean symbol are checked.
- Choose 'OK', then 'OK' again. The profile plot is shown in the results area.
Analysis
The results are shown below:
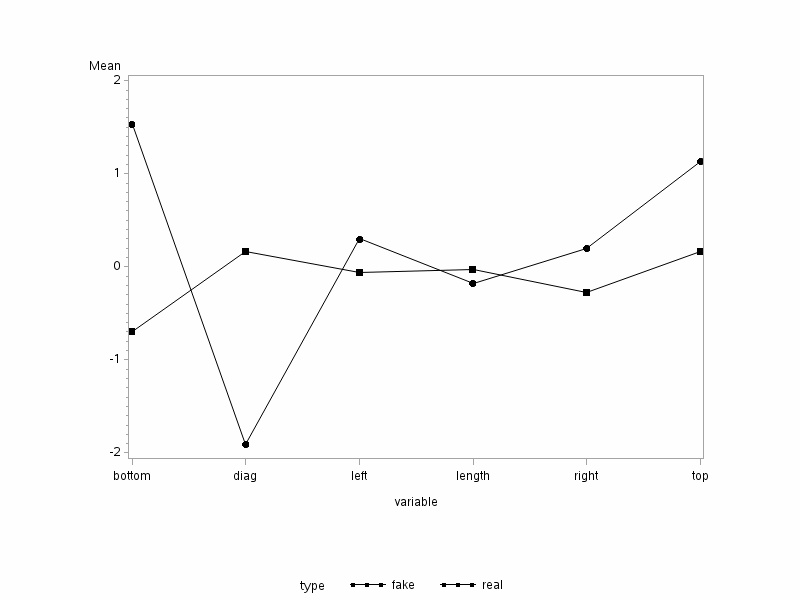
From this plot, we can see that the bottom and top margins of the counterfeit notes are larger than the corresponding mean for the genuine notes. Likewise, the left and right margins are also wider for the counterfeit notes than the genuine notes. However, the diagonal and length measurement for the counterfeit notes appears to be smaller than the genuine notes. Please note, however, this plot does not show which results are significant. The significance is from the previous simultaneous or Bonferroni confidence intervals.
One of the things to look for in these plots is if the line segments joining the dots are parallel to one another. In this case, they are not even close to being parallel for any pair of variables.
Profile Analysis
Profile Analysis is used to test the null hypothesis that these line segments are indeed parallel. You should test the hypothesis that the line segments in the profile plot are parallel to one another only if the variables have the same units of measurement. We might expect parallel segments if all of the measurements for the counterfeit notes are consistently larger than the measurements for the genuine notes by some constant.
Use the following procedure to test this null hypothesis:
Step 1: For each group, we create a new random vector \(Y_{ij}\) corresponding to the \(j^{th}\) observation from population i. The elements in this vector are the differences between the values of the successive variables as shown below:
\( \mathbf{Y}_{ij} = \left(\begin{array}{c}X_{ij2}-X_{ij1}\\X_{ij3}-X_{ij2}\\\vdots \\X_{ijp}-X_{ij,p-1}\end{array}\right)\)
Step 2: Apply the two-sample Hotelling's T-square to the data \(\mathbf{Y}_{ij}\) to test the null hypothesis that the means of the \(\mathbf{Y}_{ij}\)'s for population 1 are the same as the means of the \(\mathbf{Y}_{ij}\)'s for population 2:
\(H_0\colon \boldsymbol{\mu}_{\mathbf{Y}_1} = \boldsymbol{\mu}_{\mathbf{Y}_2}\)
7.2.6 - Model Assumptions and Diagnostics Assumptions
7.2.6 - Model Assumptions and Diagnostics AssumptionsIn carrying out any statistical analysis it is always important to consider the assumptions for the analysis and confirm that all assumptions are satisfied.
Let's recall the four assumptions underlying Hotelling's T-square test.
- The data from population i is sampled from a population with mean vector \(\boldsymbol{\mu}_{i}\).
- The data from both populations have a common variance-covariance matrix \(Σ\)
- Independence. The subjects from both populations are independently sampled.
Note! This does not mean that the variables are independent of one another
- Normality. Both populations are multivariate normally distributed.
The following will consider each of these assumptions separately, and methods for diagnosing their validity.
-
Assumption 1: The data from population i is sampled from a population mean vector \(\boldsymbol{\mu}_{i}\).
- This assumption essentially means that there are no subpopulations with a different population mean vectors.
- In our current example, this might be violated if the counterfeit notes were produced by more than one counterfeiter.
- Generally, if you have randomized experiments, this assumption is not of any concern. However, in the current application, we would have to ask the police investigators whether more than one counterfeiter might be present.
-
Assumption 2: For now we will skip Assumption 2 and return to it at a later time.
-
Assumption 3: Independence
- Says the subjects for each population were independently sampled. This does not mean that the variables are independent of one another.
- This assumption may be violated for three different reasons:
- Clustered data: If bank notes are produced in batches, then the data may be clustered. In this case, the notes sampled within a batch may be correlated with one another.
- Time-series data: If the notes are produced in some order over time, there might be some temporal correlation between notes over time. The notes produced at times close to one another may be more similar. This could result in temporal correlation violating the assumptions of the analysis.
- Spatial data: If the data were collected over space, we may encounter some spatial correlation.
Note! the results of Hotelling's T-square are not generally robust to violations of independence.
-
Assumption 4: Multivariate Normality
To assess this assumption we can produce the following diagnostic procedures:
- Produce histograms for each variable. We should look for a symmetric distribution.
- Produce scatter plots for each pair of variables. Under multivariate normality, we should see an elliptical cloud of points.
- Produce a three-dimensional rotating scatter plot. Again, we should see an elliptical cloud of points.
So, in general, Hotelling's T-square is not going to be sensitive to violations of this assumption.
Now let us return to assumption 2.
Assumption 2. The data from both populations have a common variance-covariance matrix \(Σ\).
This assumption may be assessed using Box's Test.
Box's Test
Suppose that the data from population i have variance-covariance matrix \(\Sigma_i\); for population i = 1, 2. Need to test the null hypothesis that \(\Sigma_1\) is equal to \(\Sigma_2\) against the general alternative that they are not equal as shown below:
\(H_0\colon \Sigma_1 = \Sigma_2\) against \(H_a\colon \Sigma_1 \ne \Sigma_2\)
Here, the alternative is that the variance-covariance matrices differ in at least one of their elements.
The test statistic for Box's Test is given by L-prime as shown below:
\(L' = c\{(n_1+n_2-2)\log{|\mathbf{S}_p|}- (n_1-1)\log{|\mathbf{S}_1|} - (n_2-1)\log{|\mathbf{S}_2|}\}\)
This involves a finite population correction factor c, which is given below.
The finite population correction factor, c, is given below:
\(c = 1-\dfrac{2p^2+3p-1}{6(p+1)}\left\{\dfrac{1}{n_1-1}+\dfrac{1}{n_2-1} - \dfrac{1}{n_1+n_2-2}\right\}\)
It is a function of the number of variables p, and the sample sizes \(n_{1}\) and \(n_{2}\).
Under the null hypothesis, \(H_{0}\colon \Sigma_{1} = \Sigma_{2} \), Box's test statistic is approximately chi-square distributed with p(p + 1)/2 degrees of freedom. That is,
\(L' \overset{\cdot}{\sim} \chi^2_{\dfrac{p(p+1)}{2}}\)
The degrees of freedom is equal to the number of unique elements in the variance-covariance matrix (taking into account that this matrix is symmetric). We will reject \(H_o\) at level \(\alpha\) if the test statistic exceeds the critical value from the chi-square table evaluated at level \(\alpha\).
\(L' > \chi^2_{\dfrac{p(p+1)}{2}, \alpha}\)
Box's Test may be carried out using the SAS program as shown below:
Download the SAS program here: swiss15.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Bartlett's Test - Swiss Bank Notes";
data swiss;
infile "D:\Statistics\STAT 505\data\swiss3.csv" firstobs=2 delimiter=',';
input type $ length left right bottom top diag;
run;
/* The discrim procedure is called with the pool=test
* option to produce Bartlett's test for equal
* covariance matrices. The remaining parts of the
* output are not used.
* The class statement defines the grouping variable,
* which is the type of note, and all response
* variables are specified in the var statement.
*/
proc discrim pool=test;
class type;
var length left right bottom top diag;
run;
The output can be downloaded here: swiss15.lst
At this time Minitab does not support this procedure.
Analysis
Under the null hypothesis that the variance-covariance matrices for the two populations are equal, the natural logs of the determinants of the variance-covariance matrices should be approximately the same for the fake and the real notes.
The results of Box's Test are on the bottom of page two of the output. The test statistic is 121.90 with 21 degrees of freedom; recall that p=6. The p-value for the test is less than 0.0001 indicating that we reject the null hypothesis.
The conclusion here is that the two populations of banknotes have different variance-covariance matrices in at least one of their elements. This is backed up by the evidence given by the test statistic \(\left( L ^ { \prime } = 121.899; \mathrm { d.f. } = 21 ; p < 0.0001 \right)\). Therefore, the assumption of homogeneous variance-covariance matrices is violated.
Notes
One should be aware that, even though Hotelling's T-square test is robust to violations of assumptions of multivariate normality, the results of Box's test are not robust to normality violations. The Box's Test should not be used if there is any indication that the data are not multivariate normally distributed.
In general, the two-sample Hotelling's T-square test is sensitive to violations of the assumption of homogeneity of variance-covariance matrices, this is especially the case when the sample sizes are unequal, i.e., \(n_{1}\) ≠ \(n_{2}\). If the sample sizes are equal then there doesn't tend to be all that much sensitivity and the ordinary two-sample Hotelling's T-square test can be used as usual.
7.2.7 - Testing for Equality of Mean Vectors when \(Σ_1 ≠ Σ_2\)
7.2.7 - Testing for Equality of Mean Vectors when \(Σ_1 ≠ Σ_2\)The following considers a test for equality of the population mean vectors when the variance-covariance matrices are not equal.
Here we will consider the modified Hotelling's T-square test statistic given in the expression below:
\(T^2 = \mathbf{(\bar{x}_1-\bar{x}_2)}'\left\{\dfrac{1}{n_1}\mathbf{S}_1+\dfrac{1}{n_2}\mathbf{S}_2\right\}^{-1}\mathbf{(\bar{x}_1-\bar{x}_2)}\)
Again, this is a function of the differences between the sample means for the two populations. Instead of being a function of the pooled variance-covariance matrix, we can see that the modified test statistic is written as a function of the sample variance-covariance matrix, \(\mathbf{S}_{1}\), for the first population and the sample variance-covariance matrix, \(\mathbf{S}_{2}\), for the second population. It is also a function of the sample sizes \(n_{1}\) and \(n_{2}\).
For large samples, that is if both samples are large, \(T^{2}\) is approximately chi-square distributed with p d.f. We will reject \(H_{0}\): \(\boldsymbol{\mu}_{1}\) = \(\boldsymbol{\mu}_{2}\) at level \(α\) if \(T^{2}\) exceeds the critical value from the chi-square table with p d.f. evaluated at level \(α\).
\(T^2 > \chi^2_{p, \alpha}\)
For small samples, we can calculate an F transformation as before using the formula below.
\(F = \dfrac{n_1+n_2-p-1}{p(n_1+n_2-2)}T^2\textbf{ } \overset{\cdot}{\sim}\textbf{ } F_{p,\nu}\)
This formula is a function of sample sizes \(n_{1}\) and \(n_{2}\), and the number of variables p. Under the null hypothesis, this will be F-distributed with p and approximately ν degrees of freedom, where 1 divided by ν is given by the formula below:
\( \dfrac{1}{\nu} = \sum_{i=1}^{2}\frac{1}{n_i-1} \left\{ \dfrac{\mathbf{(\bar{x}_1-\bar{x}_2)}'\mathbf{S}_T^{-1}(\dfrac{1}{n_i}\mathbf{S}_i)\mathbf{S}_T^{-1}\mathbf{(\bar{x}_1-\bar{x}_2)}}{T^2} \right\} ^2 \)
This involves summing over the two samples of banknotes, a function of the number of observations of each sample, the difference in the sample mean vectors, the sample variance-covariance matrix for each of the individual samples, as well as a new matrix \(\mathbf{S}_{T}\) which is given by the expression below:
\(\mathbf{S_T} = \dfrac{1}{n_1}\mathbf{S_1} + \dfrac{1}{n_2}\mathbf{S}_2\)
We will reject \(H_{0}\) \colon \(\mu_{1}\) = \(\mu_{2}\) at level \(α\) if the F-value exceeds the critical value from the F-table with p and ν degrees of freedom evaluated at level \(α\).
\(F > F_{p,\nu, \alpha}\)
A reference for this particular test is given in Seber, G.A.F. 1984. Multivariate Observations. Wiley, New York.
This modified version of Hotelling's T-square test can be carried out on the Swiss Bank Notes data using the SAS program below:
Download the SAS program here: swiss16.sas
View the video explanation of the SAS code.Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "2-Sample Hotellings T2 - Swiss Bank Notes (unequal variances)";
data swiss;
infile "D:\Statistics\STAT 505\data\swiss3.csv" firstobs=2 delimeter=',';
input type $ length left right bottom top diag;
run;
/* The iml code below defines and executes the 'hotel2m' module
* for calculating the two-sample Hotelling T2 test statistic,
* where here the sample covariances are not pooled.
* The commands between 'start' and 'finish' define the
* calculations of the module for two input vectors 'x1' and 'x2',
* which have the same variables but correspond to two separate groups.
* Note that s1 and s2 are not pooled in these calculations, and the
* resulting degrees of freedom are considerably more involved.
* The 'use' statement makes the 'swiss' data set available, from
* which all the variables are taken. The variables are then read
* separately into the vectors 'x1' and 'x2' for each group, and
* finally the 'hotel2' module is called.
*/
proc iml;
start hotel2m;
n1=nrow(x1);
n2=nrow(x2);
k=ncol(x1);
one1=j(n1,1,1);
one2=j(n2,1,1);
ident1=i(n1);
ident2=i(n2);
ybar1=x1`*one1/n1;
s1=x1`*(ident1-one1*one1`/n1)*x1/(n1-1.0);
print n1 ybar1;
print s1;
ybar2=x2`*one2/n2;
s2=x2`*(ident2-one2*one2`/n2)*x2/(n2-1.0);
st=s1/n1+s2/n2;
print n2 ybar2;
print s2;
t2=(ybar1-ybar2)`*inv(st)*(ybar1-ybar2);
df1=k;
p=1-probchi(t2,df1);
print t2 df1 p;
f=(n1+n2-k-1)*t2/k/(n1+n2-2);
temp=((ybar1-ybar2)`*inv(st)*(s1/n1)*inv(st)*(ybar1-ybar2)/t2)**2/(n1-1);
temp=temp+((ybar1-ybar2)`*inv(st)*(s2/n2)*inv(st)*(ybar1-ybar2)/t2)**2/(n2-1);
df2=1/temp;
p=1-probf(f,df1,df2);
print f df1 df2 p;
finish;
use swiss;
read all var{length left right bottom top diag} where (type="real") into x1;
read all var{length left right bottom top diag} where (type="fake") into x2;
run hotel2m;
The output file can be downloaded here: swiss16.lst
At this time Minitab does not support this procedure.
Analysis
As before, we are given the sample sizes for each population, the sample mean vector for each population, followed by the sample variance-covariance matrix for each population.
In the large sample approximation, we find that T-square is 2412.45 with 6 degrees of freedom, (because we have 6 variables), and a p-value that is close to 0.
- When \(n_{1}\) = \(n_{2}\), the modified values for \(T^{2}\) and F are identical to the original unmodified values obtained under the assumption of homogeneous variance-covariance matrices.
- Using the large-sample approximation, our conclusions are the same as before. We find that the mean dimensions of counterfeit notes do not match the mean dimensions of genuine Swiss banknotes. \(\left( T ^ { 2 } = 2412.45 ; \mathrm { d.f. } = 6 ; p < 0.0001 \right)\).
- Under the small-sample approximation, we also find that the mean dimensions of counterfeit notes do not match the mean dimensions of genuine Swiss banknotes. \(( F = 391.92 ; \mathrm { d } . \mathrm { f } . = 6,193 ; p < 0.0001 )\).
7.2.8 - Simultaneous (1 - α) x 100% Confidence Intervals
7.2.8 - Simultaneous (1 - α) x 100% Confidence IntervalsAs before, the next step is to determine how these notes differ. This may be carried out using the simultaneous \((1 - α) × 100\%\) confidence intervals.
For Large Samples: simultaneous \((1 - α) × 100\%\) confidence intervals may be calculated using the expression below:
\(\bar{x}_{1k} - \bar{x}_{2k} \pm \sqrt{\chi^2_{p,\alpha}\left(\dfrac{s^2_{1k}}{n_1} + \dfrac{s^2_{2k}}{n_2}\right)}\)
This involves the differences in the sample means for the kth variable, plus or minus the square root of the critical value from the chi-square table times the sum of the sample variances divided by their respective sample sizes.
For Small Samples: it is better to use the expression below:
\(\bar{x}_{1k} - \bar{x}_{2k} \pm \sqrt{\dfrac{p(n_1+n_2-2)}{n_1+n_2-p-1}F_{p,\nu,\alpha}}\sqrt{\left(\dfrac{s^2_{1k}}{n_1} + \dfrac{s^2_{2k}}{n_2}\right)}\)
Basically, the chi-square value and the square root are replaced by the critical value from the F-table, times a function of the number of variables, p, and the sample sizes n1 and n2.
Example 7-16: Swiss Bank Notes
An example of the large approximation for length is given by the hand calculation in the expression below:
\(214.969 - 214.823 \pm \sqrt{12.59 \times (\dfrac{0.15024}{100}+\dfrac{0.12401}{100})}\)
\((-0.040, 0.332)\)
Here the sample mean for the length of a genuine note was 214.969. We will subtract the sample mean for the length of a counterfeit note, 214.823. The critical value for a chi-square distribution with 6 degrees of freedom evaluated at 0.05 is 12.59. The sample variance for the first population of genuine notes is 0.15024 which we will divide by a sample size of 100. The sample variance for the second population of counterfeit notes is 0.12401 which will also divide by its sample size of 100. This yields a confidence interval that runs from -0.04 to 0.332.
The results of these calculations for each of the variables are summarized in the table below. Basically, they give us results that are comparable to the results we obtained earlier under the assumption of homogeneity for variance-covariance matrices.
| Variable | 95% Confidence Interval |
|---|---|
| Length | -0.040, 0.332 |
| Left Width | -0.515, -0.199 |
| Right Width | -0.638, -0.308 |
| Bottom Margin | -2.687, -1.763 |
| Top Margin | -1.287, -0.643 |
| Diagonal | 1.813, 2.321 |
7.2.9 - Summary of Advanced Material
7.2.9 - Summary of Advanced MaterialIn this lesson we learned about:
- Profile analysis for one-sample mean and how to carry it out in SAS
- Computing simultaneous and Bonferroni confidence intervals for the differences between sample means for each variable;
- Drawing conclusions from those confidence intervals (make sure that you indicate which population has the larger mean for each significant variable);
- Profile plots for two-sample means
- Methods for diagnosing the assumptions of the two-sample Hotelling's T-square test.
In practice, the data analyses should proceed as follows:
-
Step 1. For small samples, use histograms, scatterplots, and rotating scatterplots to assess the multivariate normality of the data. If the data do not appear to be normally distributed, apply appropriate normalizing transformations.
-
Step 2. Use Box's test to assess the assumption that the population variance-covariance matrices are homogeneous.
-
Step 3. Carry out the two-sample Hotelling's T-square test for equality of the population mean vectors. If Box's test in Step 2 is significant, use the modified two-sample Hotelling's T-square test. If the two-sample Hotelling's T-square test is not significant, conclude that there is no statistically significant evidence that the two populations have different mean vectors and stop. Otherwise, go to Step 4.
-
Step 4. Compute either simultaneous or Bonferroni confidence intervals. For the significant variables, draw conclusions regarding which population has the larger mean.