7.1.10 - Confidence Intervals
7.1.10 - Confidence IntervalsConfidence intervals for the Paired Hotelling's T-square are computed in the same way as for the one-sample Hotelling's T-square, therefore, the notes here will not be as detailed as for the one-sample. Let's review the basic procedures:
Simultaneous (1 - \(\alpha\)) × 100% Confidence Intervals for the mean differences are calculated using the expression below:
\(\bar{y}_j \pm \sqrt{\frac{p(n-1)}{n-p}F_{p,n-p,\alpha}}\sqrt{\frac{s^2_{Y_j}}{n}}\)
Bonferroni (1 - \(\alpha\)) × 100% Confidence Intervals for the mean differences are calculated using the following expression:
\(\bar{y}_j \pm t_{n-1, \frac{\alpha}{2p}}\sqrt{\frac{s^2_{Y_j}}{n}}\)
As before, simultaneous intervals will be used if we are potentially interested in confidence intervals for linear combinations among the variables of the data. Bonferroni intervals should be used if we want to simply focus on the means for each of the individual variables themselves. In this case, the individual questions.
Example 7-10: Spouse Data (Bonferroni CI)
The simultaneous Bonferroni Confidence intervals may be computed using the SAS program that can be downloaded below:
Download the Spouse 1 SAS Program: spouse1a.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Confidence Intervals - Spouse Data";
/* %let allows the p variable to be used throughout the code below
* After reading in the spouse data, where each variable is
* originally in its own column, the next statements define difference
* variables between husbands and wives, and they stack the data
* so that all group labels (1 through 4) are in one column called 'variable',
* and all differences are in another column called 'diff'.
* This format is used for the calculations that follow.
*/
%let p=4;
data spouse;
infile "D:\Statistics\STAT 505\data\spouse.csv" firstobs=2 delimiter=',';
input h1 h2 h3 h4 w1 w2 w3 w4;
variable=1; diff=h1-w1; output;
variable=2; diff=h2-w2; output;
variable=3; diff=h3-w3; output;
variable=4; diff=h4-w4; output;
drop h1 h2 h3 h4 w1 w2 w3 w4;
run;
proc sort;
by variable;
run;
/* The means procedure calculates and saves the sample size,
* mean, and variance for each variable. It then saves these results
* in a new data set 'a' for use in the final step below.
*/
proc means data=spouse noprint;
by variable;
var diff;
output out=a n=n mean=xbar var=s2;
run;
/* The data step here is used to calculate the confidence interval
* limits from the statistics calculated in the data set 'a'.
* The values 't' and'f' are the critical values used in the
* Bonferroni and F intervals, respectively.
*/
data b;
set a;
f=finv(0.95,&p,n-&p);
t=tinv(1-0.025/&p,n-1);
losim=xbar-sqrt(&p*(n-1)*f*s2/(n-&p)/n);
upsim=xbar+sqrt(&p*(n-1)*f*s2/(n-&p)/n);
lobon=xbar-t*sqrt(s2/n);
upbon=xbar+t*sqrt(s2/n);
run;
proc print data=b;
run;
In this output losim and upsim give the lower and upper bounds for the simultaneous intervals, and lobon and upbon give the lower and upper bounds for the Bonferroni interval which are copied into the table below. You should be able to find where all of these numbers are obtained.
Computing the Bonferroni CIs
To calculate Bonferroni confidence intervals for the paired differences:
- Open the ‘spouse’ data set in a new worksheet.
- Name the columns h1, h2, h3, h4, w1, w2, w3, and w4, from left to right.
- Name new columns diff1, diff2, diff3, and diff4.
- Calc > Calculator
- Highlight and select 'diff1' to move it to the 'Store result' window.
- In the Expression window, enter ‘h1’ - ‘w1’.
- Choose 'OK'. The first difference is created in the worksheet.
- Repeat step 4. for each of the other 3 differences.
- Calc > Basic Statistics > 1-sample t
- Choose ‘One or more sample’ in the first window.
- Highlight and select the 4 differences (diff1 through diff4) move them into the window on the right.
- Under ‘Options’, enter 98.75, which corresponds to 1-0.05/4, the adjusted individual confidence level for simultaneous 95% confidence with the Bonferroni method.
- Select Mean not equal to hypothesized mean.
- Select 'OK' twice. The 95% Bonferroni intervals are displayed in the results area.
Analysis
|
Question
|
Simultaneous
|
Bonferroni
|
|---|---|---|
|
1
|
-0.5127, 0.6460
|
-0.3744, 0.5078
|
|
2
|
-0.7078, 0.4412
|
-0.5707, 0.3041
|
|
3
|
-0.7788, 0.1788
|
-0.6645, 0.0645
|
|
4
|
-0.6290, 0.3623
|
-0.5107, 0.2440
|
The simultaneous confidence intervals are plotted using Profile Plots.
The downloadable SAS program for the profile plot can be obtained here: spouse1.sas.
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Profile Plot - Spouse Data";
/* %let allows the p variable to be used throughout the code below
* After reading in the spouse data, where each variable is
* originally in its own column, the next statements define difference
* variables between husbands and wives, and they stack the data
* so that all group labels (1 through 4) are in one column called 'variable',
* and all differences are in another column called 'diff'.
* This format is used for the calculations that follow.
*/
%let p=4;
data spouse;
infile "D:\Statistics\STAT 505\data\spouse.csv" firstobs=2 delimiter=','
input h1 h2 h3 h4 w1 w2 w3 w4;
variable=1; diff=h1-w1; output;
variable=2; diff=h2-w2; output;
variable=3; diff=h3-w3; output;
variable=4; diff=h4-w4; output;
drop h1 h2 h3 h4 w1 w2 w3 w4;
run;
proc sort;
by variable;
run;
/* The means procedure calculates and saves the sample size,
* mean, and variance for each variable. It then saves these results
* in a new data set 'a' for use in the final step below.
* /
proc means data=spouse;
by variable;
var diff;
output out=a n=n mean=xbar var=s2;
run;
/* The data step here is used to calculate the simultaneous
* confidence intervals based on the F-multiplier
* from the statistics calculated in the data set 'a'.
* /
data b;
set a;
f=finv(0.95,&p,n-&p);
diff=xbar; output;
diff=xbar-sqrt(&p*(n-1)*f*s2/(n-&p)/n); output;
diff=xbar+sqrt(&p*(n-1)*f*s2/(n-&p)/n); output;
run;
/* The axis commands define the size of the plotting window.
* The horizontal axis is of the variables, and the vertical
* axis is used for the confidence limits.
* The reference line of 0 corresponds to the null value of the
* difference for each variable.
* /
proc gplot data=b;
axis1 length=4 in;
axis2 length=6 in;
plot diff*variable / vaxis=axis1 haxis=axis2 vref=0 lvref=21;
symbol v=none i=hilot color=black;
run;
(Which in this case is analogous to the earlier SAS program Download here: nutrient6.sas)
Profile plots for paired differences
To construct a profile plot with confidence limits:
1. Open the ‘spouse’ data set in a new worksheet.
2. Name the columns h1, h2, h3, h4, w1, w2, w3, and w4, from left to right.
3. Name new columns diff1, diff2, diff3, and diff4.
4. Calc > Calculator
a. Highlight and select 'diff1' to move it to the 'Store result' window.
b. In the Expression window, enter ‘h1’ - ‘w1’.
c. Choose 'OK'. The first difference is created in the worksheet.
5. Repeat step 4. for each of the other 3 differences.
6. Graph > Interval plot > Multiple Y variables with categorical variables > OK
a. Highlight and select all 4 difference variables (diff1 through diff4) to move them to the Y-variables window.
b. Display Y’s > Y’s first
c. Under Options, make sure the Mean confidence interval bar and Mean symbol are checked.
d. Choose 'OK', then 'OK' again. The profile plot is shown in the results area.
Analysis
Note: The plot is given in plot1 shown below:
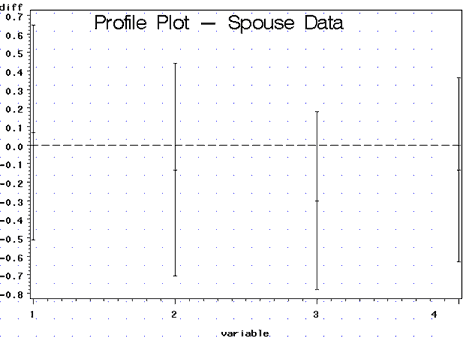
Here we can immediately notice that all of the simultaneous confidence intervals include 0 suggesting that the husbands and wives do not differ significantly in their responses to any of the questions. So what is going on here? Earlier Hotelling's \(T^{2}\) test told us that there was a significant difference between the husband and wives in their responses to the questions. But the plot of the confidence intervals suggests that there are no differences.
Basically, the significant Hotelling's T-square result is achieved through the contributions from all of the variables. It turns out that there is going to be a linear combination of the population means of the form:
\[\Psi = \sum_{j=1}^{p}c_j\mu_{Y_j}\]
whose confidence interval will not include zero.
The profile plot suggests that the largest difference occurs in response to question 3. Here, the wives respond more positively than their husbands to the question: "What is the level of companionate love you feel for your partner?"