7.2 - Advanced
7.2 - AdvancedIn this section, we touch upon some of the intricate details of inference for a multivariate population mean. The reader should be aware of these issues.
7.2.1 - Profile Analysis for One Sample Hotelling's T-Square
7.2.1 - Profile Analysis for One Sample Hotelling's T-SquareLet us revisit the original hypothesis of interest, as below
\(H_0\colon \boldsymbol{\mu} = \boldsymbol{\mu_0}\) against \(H_a\colon \boldsymbol{\mu} \ne \boldsymbol{\mu_a}\)
Note! It is equivalent to testing this null hypothesis:
\(H_0\colon \dfrac{\mu_1}{\mu^0_1} = \dfrac{\mu_2}{\mu^0_2} = \dots = \dfrac{\mu_p}{\mu^0_p} = 1\)
against the alternative that at least one of these ratios is not equal to 1, (below):
\(H_a\colon \dfrac{\mu_j}{\mu^0_j} \ne 1\) for at least one \(j \in \{1,2,\dots, p\}\)
Instead of testing the null hypothesis for the ratios of the means over their hypothesized means are all equal to one, profile analysis involves testing the null hypothesis that all of these ratios are equal to one another, but not necessarily equal to 1.
After rejecting
\(H_0\colon \dfrac{\mu_1}{\mu^0_1} = \dfrac{\mu_2}{\mu^0_2} = \dots = \dfrac{\mu_p}{\mu^0_p} = 1\)
we may wish to test
\(H_0\colon \dfrac{\mu_1}{\mu^0_1} = \dfrac{\mu_2}{\mu^0_2} = \dots = \dfrac{\mu_p}{\mu^0_p}\)
Profile Analysis can be carried out using the following procedure.
Step 1: Compute the differences between the successive ratios. That is we take the ratio of the j + 1-th variable over its hypothesized mean and subtract this from the ratio of jth variable over its hypothesized mean as shown below:
\(D_{ij} = \dfrac{X_{ij+1}}{\mu^0_{j+1}}-\dfrac{X_{ij}}{\mu^0_j}\)
We call this ratio \(D_{ij}\) for observation i.
Note! That, testing the null hypothesis that all of the ratios are equal to one another
\(H_0\colon \dfrac{\mu_1}{\mu^0_1} = \dfrac{\mu_2}{\mu^0_2} = \dots = \dfrac{\mu_p}{\mu^0_p}\)
is equivalent to testing the null hypothesis that all the mean differences are going to be equal to 0.
\(H_0\colon \boldsymbol{\mu}_D = \mathbf{0}\)
Step 2: Apply Hotelling’s \(T^{2}\) test to the data \(D_{ij}\) to test the null hypothesis that the mean of these differences is equal to 0.
\(H_0\colon \boldsymbol{\mu}_D = \mathbf{0}\)
This is carried out using the SAS program as shown below:
download the SAS Program here: nutrient8.sas
Explore the code for an explanation of the SAS code.Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Profile Analysis - Women's Nutrition Data";
/* After reading in the data, each of the original
* variables is divided by its null value to convert
* to a common scale without specific units.
* The differences are then defined for each successive
* pair of variables.
*/
data nutrient;
infile "D:\Statistics\STAT 505\data\nutrient.csv" firstobs=2 delimiter=','
input id calcium iron protein a c;
calcium=calcium/1000;
iron=iron/15;
protein=protein/60;
a=a/800;
c=c/75;
diff1=iron-calcium;
diff2=protein-iron;
diff3=a-protein;
diff4=c-a;
run;
/* The iml code to compute the hotelling t2 statistic
* is similar to that for the one-sample t2 statistic
* except that by working with differences of variable,
* the null values are all 0s, and the corresponding
* null hypothesis is that all variable means are equal
* to each other.
*/
proc iml;
start hotel;
mu0={0,0,0,0};
one=j(nrow(x),1,1);
ident=i(nrow(x));
ybar=x`*one/nrow(x);
s=x`*(ident-one*one`/nrow(x))*x/(nrow(x)-1.0);
print mu0 ybar;
print s;
t2=nrow(x)*(ybar-mu0)`*inv(s)*(ybar-mu0);
f=(nrow(x)-ncol(x))*t2/ncol(x)/(nrow(x)-1);
df1=ncol(x);
df2=nrow(x)-ncol(x);
p=1-probf(f,df1,df2);
print t2 f df1 df2 p;
finish;
use nutrient;
read all var{diff1 diff2 diff3 diff4} into x;
run hotel;
Profile analysis
To test the hypothesis of equal mean ratios:
- Open the ‘nutrient’ data set in a new worksheet.
- Name the columns id, calcium, iron, protein, vit_A, and vit_C, from left to right.
- Name new columns diff1, diff2, diff3, and diff4.
- Calc > Calculator
- Highlight and select 'diff1' to move it to the 'Store result' window.
- In the Expression window, enter ‘iron’ / 15 - ‘calcium’ / 1000, where the values 15 and 1000 come from the null values of interest for iron and calcium, respectively.
- Choose 'OK'. The difference between the iron and calcium ratios is displayed in the worksheet variable diff1.
- Calc > Calculator
- Highlight and select 'diff2' to move it to the Store result window.
- In the Expression window, enter ‘protein’ / 60 - ‘iron’ / 15, where the values 60 and 15 come from the null values of interest for protein and iron, respectively.
- Choose 'OK'. The difference between the protein and iron ratios is displayed in the worksheet variable diff2.
- Repeat step 5. for the difference between the vitamin A ratio and the protein ratio, where each ratio is obtained by dividing the original variable by its null value.
- Repeat step 5. again for the last difference, which is between the vitamin C ratio and the vitamin A ratio.
- Stat > Basic Statistics > Store Descriptive Statistics
- Highlight and select all 4 difference variables (diff1 through diff4) to move them to the 'Variables' window.
- Under Statistics, choose ‘Mean’, and then ‘OK’.
- Choose ‘OK’ again. The 4 difference means are displayed in five new columns in the worksheet.
- Data > Transpose Columns
- Highlight and select the 4 column names with the means from the step above.
- Choose ‘After last column in use’ then ‘OK'. The means are displayed in a single column in the worksheet.
- Name the new column of the numeric means ‘means’ for the remaining steps.
- Data > Copy > Columns to Matrix
- Highlight and select ‘means’ for the 'Copy from columns' window.
- Enter the ‘M1’ in the In current worksheet window. Then choose ‘OK’.
- Calc > Matrices > Transpose
- Highlight and select ‘M1’ in the 'Transpose from' window and enter ‘M2’ in the 'Store result' window.
- Choose ‘OK’.
- Stat > Basic Statistics > Covariance
- Highlight and select all 4 difference variables (diff1 through diff4) to move them to the 'Variables' window.
- Check the box to Store matrix and then choose ‘OK’. This will store the covariance matrix in a new variable ‘M3’.
- Calc > Matrices > Invert
- Highlight and select ‘M3’ to move it to the 'Invert from' window.
- Enter ‘M4’ in the 'Store result in' window and choose ‘OK’. This will store the inverted covariance matrix in a new variable ‘M4’.
- Calc > Matrices > Arithmetic
- Choose Multiply and enter M2 and M4, respectively in the two windows.
- Enter ‘M5’ as the name in the 'Store result' window and then ‘OK’.
- Calc > Matrices > Arithmetic
- Choose Multiply and enter M5 and M1, respectively in the two windows.
- Enter ‘M6’ as the name in the 'Store result' window and then ‘OK’. The answer 1.39864 is displayed in the results window.
- Calc > Calculator
- Enter C16 (or any unused column name) in the 'Store result' window.
- In the Expression window, enter 1.39864 * 737 (this is the answer from 16b times the sample size). Choose ‘OK’. The value of the T2 statistic is displayed in the worksheet under ‘C16’.
Analysis
The results yield a Hotelling's \(T^{2}\) of 1,030.7953 and an F value of 256.64843, 4, and 733 degrees of freedom, and a p-value very close to 0.
| MU0 | YBAR |
|---|---|
| 0 | 0.1179441 |
| 0 | 0.3547307 |
| 0 | -0.04718 |
| 0 | 0.0028351 |
| S | ||||
|---|---|---|---|---|
| 0.191621 | -0.071018 | 0.0451147 | -0.037562 | |
| -0.071018 | 0.1653837 | -0.178844 | 0.029556 | |
| 0.0451147 | -0.178844 | 4.123726 | -3.755071 | |
| -0.037562 | 0.029556 | -3.75507 | -3.755071 | |
| T2 | F | DF1 | DF2 | P |
|---|---|---|---|---|
| 1030.7953 | 256.64843 | 4 | 733 | 0 |
Example 7-14: Women’s Health Survey
Here we can reject the null hypothesis that the ratio of mean intake over the recommended intake is the same for each nutrient as the evidence has shown here:
\( T ^ { 2 } = 1030.80 ; F = 256.65 ; \mathrm { d.f. } = 4,733 ; p < 0.0001 \)
This null hypothesis could be true if, for example, all the women were taking in nutrients in their required ratios, but they were either eating too little or eating too much.
7.2.2 - Upon Which Variable do the Swiss Banknotes Differ? -- Two Sample Mean Problem
7.2.2 - Upon Which Variable do the Swiss Banknotes Differ? -- Two Sample Mean ProblemWhen the hypothesis of equality of two independent population means is rejected, one would like to know on account of which variable the hypothesis is rejected. To assess that, we go back to the example of Swiss Banknotes.
To assess which variable these notes differ on we will consider the \(( 1 - \alpha ) \times 100 \%\) Confidence Ellipse for the difference in the population mean vectors for the two populations of banknotes, \(\boldsymbol{\mu_{1}}\) - \(\boldsymbol{\mu_{2}}\). This ellipse is given by the set of \(\boldsymbol{\mu_{1}}\) satisfying the expression:
\(\mathbf{(\bar{x}_1-\bar{x}_2-(\pmb{\mu}_1-\pmb{\mu}_2))}'\left\{\mathbf{S}_p \left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right) \right\}^{-1}\mathbf{(\bar{x}_1-\bar{x}_2-(\pmb{\mu}_1-\pmb{\mu}_2))} \le \dfrac{p(n_1+n_2-2)}{n_1+n_2-p-1}F_{p,n_1+n_2-p-1,\alpha}\)
To understand the geometry of this ellipse, let
\(\lambda_1, \lambda_2, \dots, \lambda_p\)
denote the eigenvalues of the pooled variance-covariance matrix \(S_{p}\), and let
\(\mathbf{e}_{1}\), \(\mathbf{e}_{2}\), ..., \(\mathbf{e}_{p}\)
denote the corresponding eigenvectors. Then the \(k^{th}\) axis of this p dimensional ellipse points in the direction specified by the \(k^{th}\) eigenvector, \(\mathbf{e}_{k}\) And, it has a half-length given by the expression below:
\[l_k = \sqrt{\lambda_k\frac{p(n_1+n_2-2)}{n_1+n_2-p-1}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)F_{p,n_1+n_2-p-1,\alpha}}\]
Note, again, that this is a function of the number of variables, p, the sample sizes \(n_{1}\) and \(n_{2}\), and the critical value from the F-table.
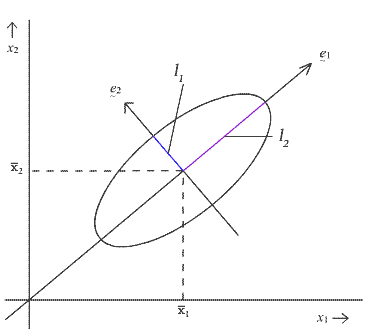
The \(( 1 - \alpha ) \times 100 \%\) confidence ellipse yields simultaneous \(( 1 - \alpha ) \times 100 \%\) confidence intervals for all linear combinations of the form given in the expression below:
\(c_1(\mu_{11}-\mu_{21})+c_2(\mu_{12}-\mu_{22})+\dots+c_p(\mu_{1p}-\mu_{2p}) = \sum_{k=1}^{p}c_k(\mu_{1k}-\mu_{2k}) = \mathbf{c'(\mu_1-\mu_k)}\)
So, these are all linear combinations of the differences in the sample means between the two populations where we are taking linear combinations across variables. These simultaneous confidence intervals are given by the expression below:
\(\sum_{k=1}^{p}c_k(\bar{x}_{1k}-\bar{x}_{2k}) \pm \sqrt{\dfrac{p(n_1+n_2-2)}{n_1+n_2-p-1}F_{p,n_1+n_2-p-1,\alpha}}\sqrt{\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right) \sum_{k=1}^{p}\sum_{l=1}^{p}c_kc_ls^{(p)}_{kl}}\)
Here, the terms \(s^{(p)}_{kl}\) denote the pooled covariances between variables k and l.
Interpretation
The interpretation of these confidence intervals is the same as that for the one sample of Hotelling's T-square. Here, we are \(( 1 - \alpha ) \times 100 \%\) confident that all of these intervals cover their respective linear combinations of the differences between the means of the two populations. In particular, we are also \(( 1 - \alpha ) \times 100 \%\) confident that all of the intervals of the individual variables also cover their respective differences between the population means. For the individual variables, if we are looking at, say, the \(k^{th}\) individual variable, then we have the difference between the sample means for that variable, k, plus or minus the same radical term that we had in the expression previously, times the standard error of that difference between the sample means for the \(k^{th}\) variable. The latter involves the inverses of the sample sizes and the pooled variance for variable k.
\(\bar{x}_{1k}-\bar{x}_{2k} \pm \sqrt{\dfrac{p(n_1+n_2-2)}{n_1+n_2-p-1}F_{p,n_1+n_2-p-1,\alpha}}\sqrt{\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right) s^2_k}\)
So, here, \(s^2_k\) is the pooled variance for variable k. These intervals are called simultaneous confidence intervals.
Let's work through an example of their calculation using the Swiss Banknotes data.
7.2.3 - Example: Swiss Banknotes
7.2.3 - Example: Swiss BanknotesExample 7-15: Swiss Banknotes
An example of the calculation of simultaneous confidence intervals using the Swiss Banknotes data is given in the expression below:
\(\bar{x}_{1k}-\bar{x}_{2k} \pm \sqrt{\frac{p(n_1+n_2-2)}{n_1+n_2-p-1}F_{p,n_1+n_2-p-1,\alpha}}\sqrt{\left(\frac{1}{n_1}+\frac{1}{n_2}\right) s^2_k}\)
Here we note that the sample sizes are both equal to 100, \(n = n_{1} = n_{2} =100\), so there is going to be a simplification of our formula inside the radicals as shown above.
Carrying out the math for the variable Length, we end up with an interval that runs from -0.044 to 0.336 as shown below.
The SAS program, below, can be used to compute the simultaneous confidence intervals for the 6 variables.
Download the SAS program here: swiss11.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Confidence Intervals - Swiss Bank Notes";
/* %let allows the p variable to be used throughout the code below
*/
%let p=6;
data swiss;
infile "D:\Statistics\STAT 505\data\swiss3.csv" firstobs=2 delimiter=','
input type $ length left right bottom top diag;
run;
/* A new data set named 'real' is created, consisting
* of only the real notes. This is used for calculation
* of the statistics needed for the last step.
* Also, where each variable is originally in its own column,
* these commands stack the data so that all variable names
* are in one column called 'variable', and all response values
* are in another column called 'x'.
*/
data real;
set swiss;
if type="real";
variable="length"; x=length; output;
variable="left"; x=left; output;
variable="right"; x=right; output;
variable="bottom"; x=bottom; output;
variable="top"; x=top; output;
variable="diagonal"; x=diag; output;
keep type variable x;
run;
proc sort;
by variable;
run;
/* The means procedure calculates and saves the sample size,
* mean, and variance for each variable. It then saves these results
* in a new data set 'pop1', corresponding to the real notes.
*/
proc means data=real noprint;
by variable;
id type;
var x;
output out=pop1 n=n1 mean=xbar1 var=s21;
/* A new data set named 'fake' is created, consisting
* of only the fake notes. This is used for calculation
* of the statistics needed for the last step.
* Also, where each variable is originally in its own column,
* these commands stack the data so that all variable names
* are in one column called 'variable', and all response values
* are in another column called 'x'.
*/
data fake;
set swiss;
if type="fake";
variable="length"; x=length; output;
variable="left"; x=left; output;
variable="right"; x=right; output;
variable="bottom"; x=bottom; output;
variable="top"; x=top; output;
variable="diagonal"; x=diag; output;
keep type variable x;
run;
proc sort;
by variable;
run;
/* The means procedure calculates and saves the sample size,
* mean, and variance for each variable. It then saves these results
* in a new data set 'pop2', corresponding to the fake notes.
*/
proc means data=fake noprint;
by variable;
id type;
var x;
output out=pop2 n=n2 mean=xbar2 var=s22;
/* This last step combines the two separate data sets to one
* and computes the 95% simultaneous confidence interval limits
* from the statistics calculated previously.
* The variances are pooled from both the real and the fake samples.
*/
data combine;
merge pop1 pop2;
by variable;
f=finv(0.95,&p,n1+n2-&p-1);
t=tinv(1-0.025/&p,n1+n2-2);
sp=((n1-1)*s21+(n2-1)*s22)/(n1+n2-2);
losim=xbar1-xbar2-sqrt(&p*(n1+n2-2)*f*(1/n1+1/n2)*sp/(n1+n2-&p-1));
upsim=xbar1-xbar2+sqrt(&p*(n1+n2-2)*f*(1/n1+1/n2)*sp/(n1+n2-&p-1));
lobon=xbar1-xbar2-t*sqrt((1/n1+1/n2)*sp);
upbon=xbar1-xbar2+t*sqrt((1/n1+1/n2)*sp);
run;
proc print data=combine;
run;
The downloadable results as listed here: swiss11.lst.
At this time Minitab does not support this procedure.
Analysis
| Obs | Variable | type | _TYPE | _FREQ_ | n1 | xbar1 | s21 | n2 | xbar1 | s22 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | bottom | fake | 0 | 100 | 100 | 8.305 | 0.41321 | 100 | 10.530 | 1.28131 |
| 2 | diagon | fake | 0 | 100 | 100 | 141.517 | 0.19981 | 100 | 139.450 | 0.31121 |
| 3 | left | fake | 0 | 100 | 100 | 129.943 | 0.13258 | 100 | 130.300 | 0.06505 |
| 4 | length | fake | 0 | 100 | 100 | 214.969 | 0.15024 | 100 | 214.823 | 0.12401 |
| 5 | right | fake | 0 | 100 | 100 | 129.720 | 0.12626 | 100 | 130.193 | 0.08894 |
| 6 | top | fake | 0 | 100 | 100 | 10.168 | 0.42119 | 100 | 11.133 | 0.40446 |
| Obs | f | t | sp | losim | upsim | lobon | upbon |
|---|---|---|---|---|---|---|---|
| 1 | 2.14580 | 2.66503 | 0.84726 | -2.69809 | 1.75191 | -2.57192 | -1.97808 |
| 2 | 2.14580 | 2.66503 | 0.2551 | 1.80720 | 2.32680 | 1.87649 | 2.25751 |
| 3 | 2.14580 | 2.66503 | 0.09881 | -0.51857 | -0.19543 | -0.47547 | -0.23853 |
| 4 | 2.14580 | 2.66503 | 0.13713 | -0.04433 | 0.33633 | 0.00643 | 0.28557 |
| 5 | 2.14580 | 2.66503 | 0.10760 | -0.64160 | -0.30440 | -0.59663 | -0.34937 |
| 6 | 2.14580 | 2.66503 |
0.41282 |
-1.29523 | -0.63477 | -1.20716 | -0.72284 |
The bounds of the simultaneous confidence intervals are given in columns for losim and upsim. Those entries are copied into the table below:
| Variable | 95% Confidence Interval |
|---|---|
| Length | -0.044, 0.336 |
| Left Width | -0.519, -0.195 |
| Right Width | -0.642, -0.304 |
| Bottom Margin | -2.698, -1.752 |
| Top Margin | -1.295, -0.635 |
| Diagonal | 1.807, 2.327 |
You need to be careful where they appear in the table in the output.
When interpreting these intervals we need to see which intervals include 0, which ones fall entirely below 0, and which ones fall entirely above 0.
The first thing that we notice is that interval for length includes 0. This suggests that we can not distinguish between the lengths of counterfeit and genuine banknotes. The intervals for both width measurements fall below 0.
Since these intervals are being calculated by taking the genuine notes minus the counterfeit notes this would suggest that the counterfeit notes are larger on these variables and we can conclude that the left and right margins of the counterfeit notes are wider than the genuine notes.
Similarly, we can conclude that the top and bottom margins of the counterfeit are also too large. Note, however, that the interval for the diagonal measurements falls entirely above 0. This suggests that the diagonal measurements of the counterfeit notes are smaller than that of the genuine notes.
Conclusions
- Counterfeit notes are too wide on both the left and right margins.
- The top and bottom margins of the counterfeit notes are too large.
- The diagonal measurement of the counterfeit notes is smaller than that of the genuine notes.
- Cannot distinguish between the lengths of counterfeit and genuine banknotes.
7.2.4 - Bonferroni Corrected (1 - α) x 100% Confidence Intervals
7.2.4 - Bonferroni Corrected (1 - α) x 100% Confidence IntervalsAs in the one-sample case, the simultaneous confidence intervals should be computed only when we are interested in linear combinations of the variables. If the only intervals of interest, however, are the confidence intervals for the individual variables with no linear combinations, then a better approach is to calculate the Bonferroni corrected confidence intervals as given in the expression below:
\(\bar{x}_{1k} - \bar{x}_{2k} \pm t_{n_1+n_2-2, \frac{\alpha}{2p}}\sqrt{s^2_k\left(\dfrac{1}{n_1}+\frac{1}{n_2}\right)}\)
Carrying out the math we end up with an interval that runs from 0.006 to 0.286 as shown below:
\(\bar{x}_{1k} - \bar{x}_{2k} \pm t_{2n-2, \frac{\alpha}{2p}}\sqrt{\frac{2s^2_k}{n}}\)
\(214.959 - 214.813 \pm \underset{2.665}{\underbrace{t_{2\times 100-2, \frac{0.05}{2 \times 6}}}}\sqrt{\dfrac{2 \times 0.137}{100}}\)
\((0.006, 0.286)\)
These calculations can also be obtained from the SAS program as shown below:
Download the SAS Program here: swiss11.sas
Looking at the data step combined and moving down, we can see that the fourth line sets t=tinv. This calculates the critical value from the t-table as desired. Then the lower and upper bounds for the Bonferroni intervals are calculated under lobon and upbon at the bottom of this data step.
The downloadable output is given here: swiss11.lst places the results in the columns for lobon and upbon.
Again, make sure you note that the variables are given in alphabetical order rather than in the original order of the data. In any case, you should be able to see where the numbers in the SAS output appear in the table below:
Computing the 2 sample Bonferroni CIs
To compute the two-sample Bonferroni CIs:
- Open the ‘swiss3’ data set in a new worksheet
- Rename the columns type, length, left, right, bottom, top, and diag.
- Calc > Basic Statistics > 2-sample t
- Choose ‘Both samples are in one column’ in the first window.
- Highlight and select length to move it to the Samples window.
- Highlight and select type to move it to the Sample IDs window.
- Under ‘Options’, enter 99.17, which corresponds to 1-0.05/6, the adjusted individual confidence level for simultaneous 95% confidence with the Bonferroni method.
- Check the box to Assume equal variances.
- Select Difference not equal for the Alternative hypothesis.
- Select ‘OK’ twice. The intervals for length are displayed in the results area.
- Repeat steps 3. and 4. for each of the other 5 variables. The six resulting intervals together may be interpreted with simultaneous 95% confidence.
Analysis
In summary, we have:
| Variable | 95% Simultaneous Confidence Intervals (Bonferroni corrected) |
|---|---|
| Length | 0.006, 0.286 |
| Left Width | -0.475, -0.239 |
| Right Width | -0.597, -0.349 |
| Bottom Margin | -2.572, -1.878 |
| Top Margin | -1.207, -0.723 |
| Diagonal | 1.876, 2.258 |
The intervals are interpreted in a way similar to before. Here we can see that:
Conclusions
- Length: Genuine notes are longer than counterfeit notes.
- Left-width and Right-width: Counterfeit notes are too wide on both the left and right margins.
- Top and Bottom margins: Counterfeit notes are too large.
- Diagonal measurement: The counterfeit notes are smaller than the genuine notes.
7.2.5 - Profile Plots
7.2.5 - Profile PlotsProfile plots provide another useful graphical summary of the data. These are only meaningful if all variables have the same units of measurement. They are not meaningful if the variables have different units of measurement. For example, some variables may be measured in grams while other variables are measured in centimeters. In this case, profile plots should not be constructed.
- In the traditional profile plot, the samples mean for each group is plotted against the variables.
- For the bank notes, it is preferable to subtract the government specifications before carrying out the analyses.
This plot can be obtained by the below:
Download the SAS Program here: swiss13b.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Profile Plot - Swiss Bank Notes";
/* After reading in the swiss data, where each variable is
* originally in its own column, the next statements stack the data
* so that all variable names are in one column called 'variable',
* and all response values minus their null values
* are in another column called 'x'.
* The subtraction is useful for plotting purposes because
* it allows for a common reference value of 0 for all variables.
*/
data swiss;
infile "D:\Statistics\STAT 505\data\swiss3.csv" firstobs=2 delimeter=',';
input type $ length left right bottom top diag;
variable="length"; x=length-215.0; output;
variable="left "; x=left-130.0; output;
variable="right "; x=right-130.0; output;
variable="bottom"; x=bottom-9.0; output;
variable="top "; x=top-10.0; output;
variable="diag "; x=diag-141.354; output;
run;
proc sort;
by type variable;
run;
/* The means procedure calculates and saves mean for
* each variable and saves the results in a new data set 'a'
* for use in the steps below.
* /
proc means data=swiss;
by type variable;
var x;
output out=a mean=xbar;
run;
/* The axis commands define the size of the plotting window.
* The horizontal axis is of the variables, and the vertical
* axis is used for the mean values.
* /
proc gplot;
axis1 length=4 in label=("Mean");
axis2 length=6 in;
plot xbar*variable=type / vaxis=axis1 haxis=axis2;
symbol1 v=J f=special h=2 i=join color=black;
symbol2 v=K f=special h=2 i=join color=black;
run;
2 sample profile plot
To compute the two-sample profile plot:
- Open the ‘swiss3’ data set in a new worksheet
- Rename the columns type, length, left, right, bottom, top, and diag.
- Name six new columns in the worksheet: length2 through diag2.
- Calc > Calculator
- Highlight and select length2 to move it to the Store result window.
- In the Expression window, enter ‘length’ - 215, where the value 215 comes from the null value of interest (government specification) for length.
- Choose 'OK'. The length2 variable is populated in the worksheet.
- Repeat step 4. for the other five variables, dividing each by its null value of interest.
- Graph > Line plot > Multiple Y’s with groups > OK
- Highlight and select all 6 variables created in steps 4 and 5 (length2 through diag2) to move them to the Y-variables window.
- Choose type for the Group variable.
- Display Y’s > Y’s first
- Under Options, make sure the Mean confidence interval bar and Mean symbol are checked.
- Choose 'OK', then 'OK' again. The profile plot is shown in the results area.
Analysis
The results are shown below:
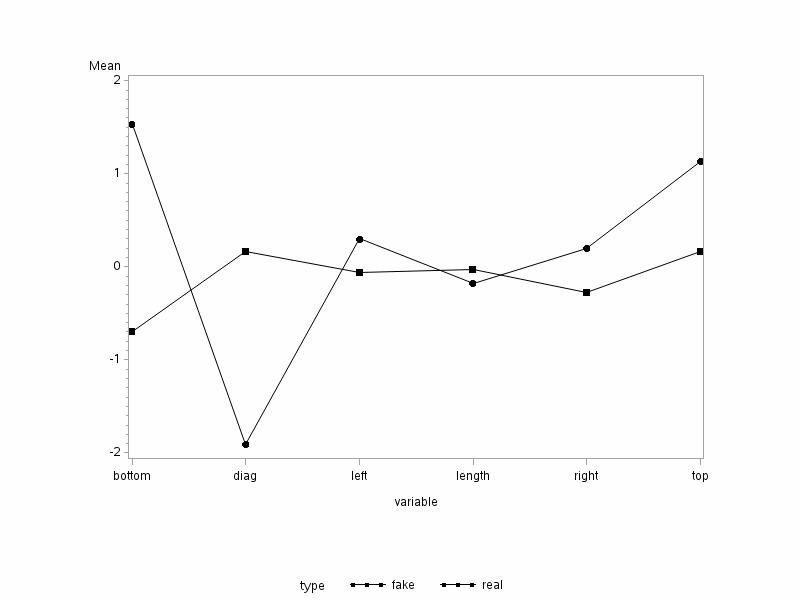
From this plot, we can see that the bottom and top margins of the counterfeit notes are larger than the corresponding mean for the genuine notes. Likewise, the left and right margins are also wider for the counterfeit notes than the genuine notes. However, the diagonal and length measurement for the counterfeit notes appears to be smaller than the genuine notes. Please note, however, this plot does not show which results are significant. The significance is from the previous simultaneous or Bonferroni confidence intervals.
One of the things to look for in these plots is if the line segments joining the dots are parallel to one another. In this case, they are not even close to being parallel for any pair of variables.
Profile Analysis
Profile Analysis is used to test the null hypothesis that these line segments are indeed parallel. You should test the hypothesis that the line segments in the profile plot are parallel to one another only if the variables have the same units of measurement. We might expect parallel segments if all of the measurements for the counterfeit notes are consistently larger than the measurements for the genuine notes by some constant.
Use the following procedure to test this null hypothesis:
Step 1: For each group, we create a new random vector \(Y_{ij}\) corresponding to the \(j^{th}\) observation from population i. The elements in this vector are the differences between the values of the successive variables as shown below:
\( \mathbf{Y}_{ij} = \left(\begin{array}{c}X_{ij2}-X_{ij1}\\X_{ij3}-X_{ij2}\\\vdots \\X_{ijp}-X_{ij,p-1}\end{array}\right)\)
Step 2: Apply the two-sample Hotelling's T-square to the data \(\mathbf{Y}_{ij}\) to test the null hypothesis that the means of the \(\mathbf{Y}_{ij}\)'s for population 1 are the same as the means of the \(\mathbf{Y}_{ij}\)'s for population 2:
\(H_0\colon \boldsymbol{\mu}_{\mathbf{Y}_1} = \boldsymbol{\mu}_{\mathbf{Y}_2}\)
7.2.6 - Model Assumptions and Diagnostics Assumptions
7.2.6 - Model Assumptions and Diagnostics AssumptionsIn carrying out any statistical analysis it is always important to consider the assumptions for the analysis and confirm that all assumptions are satisfied.
Let's recall the four assumptions underlying Hotelling's T-square test.
- The data from population i is sampled from a population with mean vector \(\boldsymbol{\mu}_{i}\).
- The data from both populations have a common variance-covariance matrix \(Σ\)
- Independence. The subjects from both populations are independently sampled.
Note! This does not mean that the variables are independent of one another
- Normality. Both populations are multivariate normally distributed.
The following will consider each of these assumptions separately, and methods for diagnosing their validity.
-
Assumption 1: The data from population i is sampled from a population mean vector \(\boldsymbol{\mu}_{i}\).
- This assumption essentially means that there are no subpopulations with a different population mean vectors.
- In our current example, this might be violated if the counterfeit notes were produced by more than one counterfeiter.
- Generally, if you have randomized experiments, this assumption is not of any concern. However, in the current application, we would have to ask the police investigators whether more than one counterfeiter might be present.
-
Assumption 2: For now we will skip Assumption 2 and return to it at a later time.
-
Assumption 3: Independence
- Says the subjects for each population were independently sampled. This does not mean that the variables are independent of one another.
- This assumption may be violated for three different reasons:
- Clustered data: If bank notes are produced in batches, then the data may be clustered. In this case, the notes sampled within a batch may be correlated with one another.
- Time-series data: If the notes are produced in some order over time, there might be some temporal correlation between notes over time. The notes produced at times close to one another may be more similar. This could result in temporal correlation violating the assumptions of the analysis.
- Spatial data: If the data were collected over space, we may encounter some spatial correlation.
Note! the results of Hotelling's T-square are not generally robust to violations of independence.
-
Assumption 4: Multivariate Normality
To assess this assumption we can produce the following diagnostic procedures:
- Produce histograms for each variable. We should look for a symmetric distribution.
- Produce scatter plots for each pair of variables. Under multivariate normality, we should see an elliptical cloud of points.
- Produce a three-dimensional rotating scatter plot. Again, we should see an elliptical cloud of points.
So, in general, Hotelling's T-square is not going to be sensitive to violations of this assumption.
Now let us return to assumption 2.
Assumption 2. The data from both populations have a common variance-covariance matrix \(Σ\).
This assumption may be assessed using Box's Test.
Box's Test
Suppose that the data from population i have variance-covariance matrix \(\Sigma_i\); for population i = 1, 2. Need to test the null hypothesis that \(\Sigma_1\) is equal to \(\Sigma_2\) against the general alternative that they are not equal as shown below:
\(H_0\colon \Sigma_1 = \Sigma_2\) against \(H_a\colon \Sigma_1 \ne \Sigma_2\)
Here, the alternative is that the variance-covariance matrices differ in at least one of their elements.
The test statistic for Box's Test is given by L-prime as shown below:
\(L' = c\{(n_1+n_2-2)\log{|\mathbf{S}_p|}- (n_1-1)\log{|\mathbf{S}_1|} - (n_2-1)\log{|\mathbf{S}_2|}\}\)
This involves a finite population correction factor c, which is given below.
The finite population correction factor, c, is given below:
\(c = 1-\dfrac{2p^2+3p-1}{6(p+1)}\left\{\dfrac{1}{n_1-1}+\dfrac{1}{n_2-1} - \dfrac{1}{n_1+n_2-2}\right\}\)
It is a function of the number of variables p, and the sample sizes \(n_{1}\) and \(n_{2}\).
Under the null hypothesis, \(H_{0}\colon \Sigma_{1} = \Sigma_{2} \), Box's test statistic is approximately chi-square distributed with p(p + 1)/2 degrees of freedom. That is,
\(L' \overset{\cdot}{\sim} \chi^2_{\dfrac{p(p+1)}{2}}\)
The degrees of freedom is equal to the number of unique elements in the variance-covariance matrix (taking into account that this matrix is symmetric). We will reject \(H_o\) at level \(\alpha\) if the test statistic exceeds the critical value from the chi-square table evaluated at level \(\alpha\).
\(L' > \chi^2_{\dfrac{p(p+1)}{2}, \alpha}\)
Box's Test may be carried out using the SAS program as shown below:
Download the SAS program here: swiss15.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Bartlett's Test - Swiss Bank Notes";
data swiss;
infile "D:\Statistics\STAT 505\data\swiss3.csv" firstobs=2 delimiter=',';
input type $ length left right bottom top diag;
run;
/* The discrim procedure is called with the pool=test
* option to produce Bartlett's test for equal
* covariance matrices. The remaining parts of the
* output are not used.
* The class statement defines the grouping variable,
* which is the type of note, and all response
* variables are specified in the var statement.
*/
proc discrim pool=test;
class type;
var length left right bottom top diag;
run;
The output can be downloaded here: swiss15.lst
At this time Minitab does not support this procedure.
Analysis
Under the null hypothesis that the variance-covariance matrices for the two populations are equal, the natural logs of the determinants of the variance-covariance matrices should be approximately the same for the fake and the real notes.
The results of Box's Test are on the bottom of page two of the output. The test statistic is 121.90 with 21 degrees of freedom; recall that p=6. The p-value for the test is less than 0.0001 indicating that we reject the null hypothesis.
The conclusion here is that the two populations of banknotes have different variance-covariance matrices in at least one of their elements. This is backed up by the evidence given by the test statistic \(\left( L ^ { \prime } = 121.899; \mathrm { d.f. } = 21 ; p < 0.0001 \right)\). Therefore, the assumption of homogeneous variance-covariance matrices is violated.
Notes
One should be aware that, even though Hotelling's T-square test is robust to violations of assumptions of multivariate normality, the results of Box's test are not robust to normality violations. The Box's Test should not be used if there is any indication that the data are not multivariate normally distributed.
In general, the two-sample Hotelling's T-square test is sensitive to violations of the assumption of homogeneity of variance-covariance matrices, this is especially the case when the sample sizes are unequal, i.e., \(n_{1}\) ≠ \(n_{2}\). If the sample sizes are equal then there doesn't tend to be all that much sensitivity and the ordinary two-sample Hotelling's T-square test can be used as usual.
7.2.7 - Testing for Equality of Mean Vectors when \(Σ_1 ≠ Σ_2\)
7.2.7 - Testing for Equality of Mean Vectors when \(Σ_1 ≠ Σ_2\)The following considers a test for equality of the population mean vectors when the variance-covariance matrices are not equal.
Here we will consider the modified Hotelling's T-square test statistic given in the expression below:
\(T^2 = \mathbf{(\bar{x}_1-\bar{x}_2)}'\left\{\dfrac{1}{n_1}\mathbf{S}_1+\dfrac{1}{n_2}\mathbf{S}_2\right\}^{-1}\mathbf{(\bar{x}_1-\bar{x}_2)}\)
Again, this is a function of the differences between the sample means for the two populations. Instead of being a function of the pooled variance-covariance matrix, we can see that the modified test statistic is written as a function of the sample variance-covariance matrix, \(\mathbf{S}_{1}\), for the first population and the sample variance-covariance matrix, \(\mathbf{S}_{2}\), for the second population. It is also a function of the sample sizes \(n_{1}\) and \(n_{2}\).
For large samples, that is if both samples are large, \(T^{2}\) is approximately chi-square distributed with p d.f. We will reject \(H_{0}\): \(\boldsymbol{\mu}_{1}\) = \(\boldsymbol{\mu}_{2}\) at level \(α\) if \(T^{2}\) exceeds the critical value from the chi-square table with p d.f. evaluated at level \(α\).
\(T^2 > \chi^2_{p, \alpha}\)
For small samples, we can calculate an F transformation as before using the formula below.
\(F = \dfrac{n_1+n_2-p-1}{p(n_1+n_2-2)}T^2\textbf{ } \overset{\cdot}{\sim}\textbf{ } F_{p,\nu}\)
This formula is a function of sample sizes \(n_{1}\) and \(n_{2}\), and the number of variables p. Under the null hypothesis, this will be F-distributed with p and approximately ν degrees of freedom, where 1 divided by ν is given by the formula below:
\( \dfrac{1}{\nu} = \sum_{i=1}^{2}\frac{1}{n_i-1} \left\{ \dfrac{\mathbf{(\bar{x}_1-\bar{x}_2)}'\mathbf{S}_T^{-1}(\dfrac{1}{n_i}\mathbf{S}_i)\mathbf{S}_T^{-1}\mathbf{(\bar{x}_1-\bar{x}_2)}}{T^2} \right\} ^2 \)
This involves summing over the two samples of banknotes, a function of the number of observations of each sample, the difference in the sample mean vectors, the sample variance-covariance matrix for each of the individual samples, as well as a new matrix \(\mathbf{S}_{T}\) which is given by the expression below:
\(\mathbf{S_T} = \dfrac{1}{n_1}\mathbf{S_1} + \dfrac{1}{n_2}\mathbf{S}_2\)
We will reject \(H_{0}\) \colon \(\mu_{1}\) = \(\mu_{2}\) at level \(α\) if the F-value exceeds the critical value from the F-table with p and ν degrees of freedom evaluated at level \(α\).
\(F > F_{p,\nu, \alpha}\)
A reference for this particular test is given in Seber, G.A.F. 1984. Multivariate Observations. Wiley, New York.
This modified version of Hotelling's T-square test can be carried out on the Swiss Bank Notes data using the SAS program below:
Download the SAS program here: swiss16.sas
View the video explanation of the SAS code.Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "2-Sample Hotellings T2 - Swiss Bank Notes (unequal variances)";
data swiss;
infile "D:\Statistics\STAT 505\data\swiss3.csv" firstobs=2 delimeter=',';
input type $ length left right bottom top diag;
run;
/* The iml code below defines and executes the 'hotel2m' module
* for calculating the two-sample Hotelling T2 test statistic,
* where here the sample covariances are not pooled.
* The commands between 'start' and 'finish' define the
* calculations of the module for two input vectors 'x1' and 'x2',
* which have the same variables but correspond to two separate groups.
* Note that s1 and s2 are not pooled in these calculations, and the
* resulting degrees of freedom are considerably more involved.
* The 'use' statement makes the 'swiss' data set available, from
* which all the variables are taken. The variables are then read
* separately into the vectors 'x1' and 'x2' for each group, and
* finally the 'hotel2' module is called.
*/
proc iml;
start hotel2m;
n1=nrow(x1);
n2=nrow(x2);
k=ncol(x1);
one1=j(n1,1,1);
one2=j(n2,1,1);
ident1=i(n1);
ident2=i(n2);
ybar1=x1`*one1/n1;
s1=x1`*(ident1-one1*one1`/n1)*x1/(n1-1.0);
print n1 ybar1;
print s1;
ybar2=x2`*one2/n2;
s2=x2`*(ident2-one2*one2`/n2)*x2/(n2-1.0);
st=s1/n1+s2/n2;
print n2 ybar2;
print s2;
t2=(ybar1-ybar2)`*inv(st)*(ybar1-ybar2);
df1=k;
p=1-probchi(t2,df1);
print t2 df1 p;
f=(n1+n2-k-1)*t2/k/(n1+n2-2);
temp=((ybar1-ybar2)`*inv(st)*(s1/n1)*inv(st)*(ybar1-ybar2)/t2)**2/(n1-1);
temp=temp+((ybar1-ybar2)`*inv(st)*(s2/n2)*inv(st)*(ybar1-ybar2)/t2)**2/(n2-1);
df2=1/temp;
p=1-probf(f,df1,df2);
print f df1 df2 p;
finish;
use swiss;
read all var{length left right bottom top diag} where (type="real") into x1;
read all var{length left right bottom top diag} where (type="fake") into x2;
run hotel2m;
The output file can be downloaded here: swiss16.lst
At this time Minitab does not support this procedure.
Analysis
As before, we are given the sample sizes for each population, the sample mean vector for each population, followed by the sample variance-covariance matrix for each population.
In the large sample approximation, we find that T-square is 2412.45 with 6 degrees of freedom, (because we have 6 variables), and a p-value that is close to 0.
- When \(n_{1}\) = \(n_{2}\), the modified values for \(T^{2}\) and F are identical to the original unmodified values obtained under the assumption of homogeneous variance-covariance matrices.
- Using the large-sample approximation, our conclusions are the same as before. We find that the mean dimensions of counterfeit notes do not match the mean dimensions of genuine Swiss banknotes. \(\left( T ^ { 2 } = 2412.45 ; \mathrm { d.f. } = 6 ; p < 0.0001 \right)\).
- Under the small-sample approximation, we also find that the mean dimensions of counterfeit notes do not match the mean dimensions of genuine Swiss banknotes. \(( F = 391.92 ; \mathrm { d } . \mathrm { f } . = 6,193 ; p < 0.0001 )\).
7.2.8 - Simultaneous (1 - α) x 100% Confidence Intervals
7.2.8 - Simultaneous (1 - α) x 100% Confidence IntervalsAs before, the next step is to determine how these notes differ. This may be carried out using the simultaneous \((1 - α) × 100\%\) confidence intervals.
For Large Samples: simultaneous \((1 - α) × 100\%\) confidence intervals may be calculated using the expression below:
\(\bar{x}_{1k} - \bar{x}_{2k} \pm \sqrt{\chi^2_{p,\alpha}\left(\dfrac{s^2_{1k}}{n_1} + \dfrac{s^2_{2k}}{n_2}\right)}\)
This involves the differences in the sample means for the kth variable, plus or minus the square root of the critical value from the chi-square table times the sum of the sample variances divided by their respective sample sizes.
For Small Samples: it is better to use the expression below:
\(\bar{x}_{1k} - \bar{x}_{2k} \pm \sqrt{\dfrac{p(n_1+n_2-2)}{n_1+n_2-p-1}F_{p,\nu,\alpha}}\sqrt{\left(\dfrac{s^2_{1k}}{n_1} + \dfrac{s^2_{2k}}{n_2}\right)}\)
Basically, the chi-square value and the square root are replaced by the critical value from the F-table, times a function of the number of variables, p, and the sample sizes n1 and n2.
Example 7-16: Swiss Bank Notes
An example of the large approximation for length is given by the hand calculation in the expression below:
\(214.969 - 214.823 \pm \sqrt{12.59 \times (\dfrac{0.15024}{100}+\dfrac{0.12401}{100})}\)
\((-0.040, 0.332)\)
Here the sample mean for the length of a genuine note was 214.969. We will subtract the sample mean for the length of a counterfeit note, 214.823. The critical value for a chi-square distribution with 6 degrees of freedom evaluated at 0.05 is 12.59. The sample variance for the first population of genuine notes is 0.15024 which we will divide by a sample size of 100. The sample variance for the second population of counterfeit notes is 0.12401 which will also divide by its sample size of 100. This yields a confidence interval that runs from -0.04 to 0.332.
The results of these calculations for each of the variables are summarized in the table below. Basically, they give us results that are comparable to the results we obtained earlier under the assumption of homogeneity for variance-covariance matrices.
| Variable | 95% Confidence Interval |
|---|---|
| Length | -0.040, 0.332 |
| Left Width | -0.515, -0.199 |
| Right Width | -0.638, -0.308 |
| Bottom Margin | -2.687, -1.763 |
| Top Margin | -1.287, -0.643 |
| Diagonal | 1.813, 2.321 |
7.2.9 - Summary of Advanced Material
7.2.9 - Summary of Advanced MaterialIn this lesson we learned about:
- Profile analysis for one-sample mean and how to carry it out in SAS
- Computing simultaneous and Bonferroni confidence intervals for the differences between sample means for each variable;
- Drawing conclusions from those confidence intervals (make sure that you indicate which population has the larger mean for each significant variable);
- Profile plots for two-sample means
- Methods for diagnosing the assumptions of the two-sample Hotelling's T-square test.
In practice, the data analyses should proceed as follows:
-
Step 1. For small samples, use histograms, scatterplots, and rotating scatterplots to assess the multivariate normality of the data. If the data do not appear to be normally distributed, apply appropriate normalizing transformations.
-
Step 2. Use Box's test to assess the assumption that the population variance-covariance matrices are homogeneous.
-
Step 3. Carry out the two-sample Hotelling's T-square test for equality of the population mean vectors. If Box's test in Step 2 is significant, use the modified two-sample Hotelling's T-square test. If the two-sample Hotelling's T-square test is not significant, conclude that there is no statistically significant evidence that the two populations have different mean vectors and stop. Otherwise, go to Step 4.
-
Step 4. Compute either simultaneous or Bonferroni confidence intervals. For the significant variables, draw conclusions regarding which population has the larger mean.