Lesson 14: Cluster Analysis
Lesson 14: Cluster AnalysisOverview
Cluster analysis is a data exploration (mining) tool for dividing a multivariate dataset into “natural” clusters (groups). We use the methods to explore whether previously undefined clusters (groups) exist in the dataset. For instance, a marketing department may wish to use survey results to sort its customers into categories (perhaps those likely to be most receptive to buying a product, those most likely to be against buying a product, and so forth).
Cluster Analysis is used when we believe that the sample units come from an unknown number of distinct populations or sub-populations. We also assume that the sample units come from a number of distinct populations, but there is no apriori definition of those populations. Our objective is to describe those populations with the observed data.
Cluster Analysis, until relatively recently, has had very little interest. This has changed because of the interest in bioinformatics and genome research. We will use an ecological example in our lesson.
Objectives
- Carry out cluster analysis using SAS or Minitab;
- Use a dendrogram to partition the data into clusters of known composition;
- Carry out post hoc analyses to describe differences among clusters.
14.1 - Example: Woodyard Hammock Data
14.1 - Example: Woodyard Hammock DataExample 14-1: Woodyard Hammock Data
We illustrate the various methods of cluster analysis using ecological data from Woodyard Hammock, a beech-magnolia forest in northern Florida. The data involve counts of the number of trees of each species in n = 72 sites. A total of 31 species were identified and counted, however, only p = 13 of the most common species were retained and are listed below. They are:
| Variable | Scientific Name | Common Name |
|---|---|---|
| carcar | Carpinus caroliniana | Ironwood |
| corflo | Cornus florida | Dogwood |
| faggra | Fagus grandifolia | Beech |
| ileopa | Ilex opaca | Holly |
| liqsty | Liquidambar styraciflua | Sweetgum |
| maggra | Magnolia grandiflora | Magnolia |
| nyssyl | Nyssa sylvatica | Blackgum |
| ostvir | Ostrya virginiana | Blue Beech |
| oxyarb | Oxydendrum arboreum | Sourwood |
| pingla | Pinus glabra | Spruce Pine |
| quenig | Quercus nigra | Water Oak |
| quemic | Quercus michauxii | Swamp Chestnut Oak |
| symtin | Symplocus tinctoria | Horse Sugar |
The first column gives the 6-letter code identifying the species, the second column gives its scientific name (Latin binomial), and the third column gives the common name for each species. The most commonly found of these species were the beech and magnolia.
What is our objective with this data?
We hope to group sample sites together into clusters that share similar species compositions as determined by some measure of association. There are several options to measure association. Two common measures are listed below:
-
The measure of Association between Sample Units: We need some way to measure how similar two subjects or objects are to one another. This could be just about any type of measure of association. There is a lot of room for creativity here. However, SAS only allows Euclidean distance (defined later).
-
The measure of Association between Clusters: How similar are two clusters? There are dozens of techniques that can be used here.
Many different approaches to the cluster analysis problem have been proposed. The approaches generally fall into three broad categories:
-
Hierarchical methods
- In agglomerative hierarchical algorithms, we start by defining each data point as a cluster. Then, the two closest clusters are combined into a new cluster. In each subsequent step, two existing clusters are merged into a single cluster.
- In divisive hierarchical algorithms, we start by putting all data points into a single cluster. Then we divide this cluster into two clusters. At each subsequent step, we divide an existing cluster into two clusters.
Note 1: Agglomerative methods are used much more often than divisive methods.Note 2: Hierarchical methods can be adapted to cluster variables rather than observations. This is a common use for hierarchical methods.
-
Non-hierarchical methods:
- In a non-hierarchical method, the data are initially partitioned into a set of K clusters. This may be a random partition or a partition based on a first “good” guess at seed points which form the initial centers of the clusters. The data points are iteratively moved into different clusters until there is no sensible reassignment possible. The initial number of clusters (K) may be specified by the user or by the software algorithm.
- The most commonly used non-hierarchical method is MacQueen’s K-means method.
-
Model-based methods:
- A model-based method uses a mixture model to specify the density function of the x-variables. In a mixture model, a population is modeled as a mixture of different subpopulations, each with the same general form for its probability density function and possibly different values for parameters, such as the mean vector. For instance, the model may be a mixture of multivariate normal distributions. In cluster analysis, the algorithm provides a partition of the dataset that maximizes the likelihood function as defined by the mixture model. We won’t cover this method any further in this course unit.
14.2 - Measures of Association for Continuous Variables
14.2 - Measures of Association for Continuous VariablesWe use the standard notation that we have been using all along:
- \(X_{ik}\) = Response for variable k in sample unit i (the number of individual species k at site i)
- \(n\) = Number of sample units
- \(p\) = Number of variables
Johnson and Wichern list four different measures of association (similarity) that are frequently used with continuous variables in cluster analysis:
Some other distances also use a similar concept.
-
Euclidean Distance
This is used most commonly. For instance, in two dimensions, we can plot the observations in a scatter plot, and simply measure the distances between the pairs of points. More generally we can use the following equation:
\(d(\mathbf{X_i, X_j}) = \sqrt{\sum\limits_{k=1}^{p}(X_{ik} - X_{jk})^2}\)
This is the square root of the sum of the squared differences between the measurements for each variable. (This is the only method that is available in SAS. In Minitab there are other distances like Pearson, Squared Euclidean, etc.)
-
Minkowski Distance
\(d(\mathbf{X_i, X_j}) = \left[\sum\limits_{k=1}^{p}|X_{ik}-X_{jk}|^m\right]^{1/m}\)
Here the square is replaced by raising the difference by a power of m and instead of taking the square root, we take the mth root.
Here are two other methods for measuring association:
-
Canberra Metric
\(d(\mathbf{X_i, X_j}) = \sum\limits_{k=1}^{p}\frac{|X_{ik}-X_{jk}|}{X_{ik}+X_{jk}}\)
-
Czekanowski Coefficient
\(d(\mathbf{X_i, X_j}) = 1- \frac{2\sum\limits_{k=1}^{p}\text{min}(X_{ik},X_{jk})}{\sum\limits_{k=1}^{p}(X_{ik}+X_{jk})}\)
For each distance measure, similar subjects have smaller distances than dissimilar subjects. Similar subjects are more strongly associated.
Or, if you like, you can invent your own measure! However, whatever you invent, the measure of association must satisfy the following properties:
-
Symmetry
\(d(\mathbf{X_i, X_j}) = d(\mathbf{X_j, X_i})\)
i.e., the distance between subject one and subject two must be the same as the distance between subject two and subject one. -
Positivity
\(d(\mathbf{X_i, X_j}) > 0\) if \(\mathbf{X_i} \ne \mathbf{X_j}\)
...the distances must be positive - negative distances are not allowed! -
Identity
\(d(\mathbf{X_i, X_j}) = 0\) if \(\mathbf{X_i} = \mathbf{X_j}\)
...the distance between the subject and itself should be zero. - Triangle inequality
\(d(\mathbf{X_i, X_k}) \le d(\mathbf{X_i, X_j}) +d(\mathbf{X_j, X_k}) \)
This follows from a geometric consideration, that is the sum of two sides of a triangle cannot be smaller than the third side.
14.3 - Measures of Association for Binary Variables
14.3 - Measures of Association for Binary VariablesIn the Woodyard Hammock example, the observer recorded how many individuals belong to each species at each site. However, other research methods might only record whether or not the species was present at a site. In sociological studies, we might look at traits that some people have and others do not. Typically 1(0) signifies that the trait of interest is present (absent).
For sample units i and j, consider the following contingency table of frequencies of 1-1, 1-0, 0-1, and 0-0 matches across the variables:
| Unit j | ||||
|---|---|---|---|---|
| Unit i | 1 | 0 | Total | |
| 1 | a | b | a + b | |
| 0 | c | d | c + d | |
| Total | a + c | b + d | p = a + b + c + d | |
If we are comparing two subjects, subject I, and subject j, then a is the number of variables present for both subjects. In the Woodyard Hammock example, this is the number of species found at both sites. Similarly, b is the number (of species) found in subject i but not subject j, c is just the opposite, and d is the number that is not found in either subject.
From here we can calculate row totals, column totals, and a grand total.
Johnson and Wichern list the following Similarity Coefficients used for binary data:
| Coefficient | Rationale |
|---|---|
| \( \dfrac { a + d } { p }\) | Equal weights for 1-1, 0-0 matches |
| \( \dfrac { 2 ( a + d ) } { 2 ( a + d ) + b + c }\) | Double weights for 1-, 0-0 matches |
| \( \dfrac { a + d } { a + d + 2 ( b + c ) }\) | Double weights for unmatched pairs |
| \( \dfrac { a } { p }\) | Proportion of 1-1 matches |
| \( \dfrac { a } { a + b + c }\) | 0-0 matches are irrelevant |
| \( \dfrac { 2 a } { 2 a + b + c }\) |
0-0 matches are irrelevant Double weights for 1-1 matches |
| \( \dfrac { a } { a + 2 ( b + c ) }\) | 0-0 matches are irrelevant |
| \( \dfrac { a } { b + c }\) |
Double weights for unmatched pairs Ratio of 1-1 matches to mismatches |
The first coefficient looks at the number of matches (1-1 or 0-0) and divides it by the total number of variables. If two sites have identical species lists, then this coefficient is equal to one because c = b = 0. The more species that are found at one and only one of the two sites, the smaller the value for this coefficient. If no species in one site are found in the other site, then this coefficient takes a value of zero because a = d = 0.
The remaining coefficients give different weights to matched (1-1 or 0-0) or mismatched (1-0 or 0-1) pairs. For example, the second coefficient gives matched pairs double the weight and thus emphasizes agreements in the species lists. In contrast, the third coefficient gives mismatched pairs double the weight, more strongly penalizing disagreements between the species lists. The remaining coefficients ignore species not found in either site.
The choice of coefficient will have an impact on the results of the analysis. Coefficients may be selected based on theoretical considerations specific to the problem at hand, or so as to yield the most parsimonious description of the data. For the latter, the analysis may be repeated using several of these coefficients. The coefficient that yields the most easily interpreted results is selected.
The main thing is that you need some measure of association between your subjects before the analysis can proceed. We will look next at methods of measuring distances between clusters.
14.4 - Agglomerative Hierarchical Clustering
14.4 - Agglomerative Hierarchical ClusteringCombining Clusters in the Agglomerative Approach
In the agglomerative hierarchical approach, we define each data point as a cluster and combine existing clusters at each step. Here are four different methods for this approach:
-
Single Linkage: In single linkage, we define the distance between two clusters as the minimum distance between any single data point in the first cluster and any single data point in the second cluster. On the basis of this definition of distance between clusters, at each stage of the process, we combine the two clusters with the smallest single linkage distance.
-
Complete Linkage: In complete linkage, we define the distance between two clusters to be the maximum distance between any single data point in the first cluster and any single data point in the second cluster. On the basis of this definition of distance between clusters, at each stage of the process, we combine the two clusters that have the smallest complete linkage distance.
-
Average Linkage: In average linkage, we define the distance between two clusters to be the average distance between data points in the first cluster and data points in the second cluster. On the basis of this definition of distance between clusters, at each stage of the process we combine the two clusters that have the smallest average linkage distance.
-
Centroid Method: In the centroid method, the distance between two clusters is the distance between the two mean vectors of the clusters. At each stage of the process we combine the two clusters that have the smallest centroid distance.
-
Ward’s Method: This method does not directly define a measure of distance between two points or clusters. It is an ANOVA-based approach. One-way univariate ANOVAs are done for each variable with groups defined by the clusters at that stage of the process. At each stage, two clusters merge that provide the smallest increase in the combined error sum of squares.
In the following table, the mathematical form of the distances is provided. The graph gives a geometric interpretation.
Notationally, define
- \(\boldsymbol{X _ { 1 , } X _ { 2 , } , \dots , X _ { k }}\) = Observations from cluster 1
- \(\boldsymbol{Y _ { 1 , } Y _ { 2 , } , \dots , Y _ { l }}\) = Observations from cluster 2
- d(x,y) = Distance between a subject with observation vector x and a subject with observation vector y
Linkage Methods or Measuring Association d12 Between Clusters 1 and 2
| Single Linkage | \(d_{12} = \displaystyle \min_{i,j}\text{ } d(\mathbf{X}_i, \mathbf{Y}_j)\) | This is the distance between the closest members of the two clusters. |
|---|---|---|
| Complete Linkage | \(d_{12} = \displaystyle \max_{i,j}\text{ } d(\mathbf{X}_i, \mathbf{Y}_j)\) | This is the distance between the members that are farthest apart (most dissimilar) |
| Average Linkage | \(d_{12} = \frac{1}{kl}\sum\limits_{i=1}^{k}\sum\limits_{j=1}^{l}d(\mathbf{X}_i, \mathbf{Y}_j)\) | This method involves looking at the distances between all pairs and averages all of these distances. This is also called UPGMA - Unweighted Pair Group Mean Averaging. |
| Centroid Method |
\( d_{12} = d(\bar{\mathbf{x}},\bar{\mathbf{y}})\) |
This involves finding the mean vector location for each of the clusters and taking the distance between the two centroids. |
The following video shows the linkage method types listed on the right for a visual representation of how the distances are determined for each method.
14.5 - Agglomerative Method Example
14.5 - Agglomerative Method ExampleExample: Woodyard Hammock Data
SAS uses the Euclidian distance metric and agglomerative clustering, while Minitab can use Manhattan, Pearson, Squared Euclidean, and Squared Pearson distances as well. Both SAS and Minitab use only agglomerative clustering.
Use the datafile wood.csv.
Cluster analysis is carried out in SAS using a cluster analysis procedure that is abbreviated as a cluster. We will look at how this is carried out in the SAS program below.
options ls=78;
title 'Cluster Analysis - Woodyard Hammock - Complete Linkage';
data wood;
infile 'D:\Statistics\STAT 505\data\wood.csv' firstobs=2 delimiter=',';
input x y acerub carcar carcor cargla cercan corflo faggra frapen
ileopa liqsty lirtul maggra magvir morrub nyssyl osmame ostvir
oxyarb pingla pintae pruser quealb quehem quenig quemic queshu quevir
symtin ulmala araspi cyrrac;
ident=_n_;
drop acerub carcor cargla cercan frapen lirtul magvir morrub osmame pintae
pruser quealb quehem queshu quevir ulmala araspi cyrrac;
run;
proc sort data=wood;
by ident;
run;
proc cluster data=wood method=complete outtree=clust1;
var carcar corflo faggra ileopa liqsty maggra nyssyl ostvir oxyarb
pingla quenig quemic symtin;
id ident;
run;
proc tree data=clust1 horizontal nclusters=6 out=clust2;
id ident;
run;
proc sort data=clust2;
by ident;
run;
proc print data=clust2;
run;
data combine;
merge wood clust2;
by ident;
run;
proc glm data=combine;
class cluster;
model carcar corflo faggra ileopa liqsty maggra nyssyl ostvir oxyarb
pingla quenig quemic symtin = cluster;
means cluster;
run;
Download the SAS Program here: wood1.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title 'Cluster Analysis - Woodyard Hammock - Complete Linkage';
/* After reading in the data, an ident variable is created as the
* row number for each observation. This is neeed for the clustering algorithm.
* The drop statement removes several variables not used for this analysis.
*/
data wood;
infile 'D:\Statistics\STAT 505\data\wood.csv' firstobs=2 delimiter=',';
input x y acerub carcar carcor cargla cercan corflo faggra frapen
ileopa liqsty lirtul maggra magvir morrub nyssyl osmame ostvir
oxyarb pingla pintae pruser quealb quehem quenig quemic queshu quevir
symtin ulmala araspi cyrrac;
ident=_n_;
drop acerub carcor cargla cercan frapen lirtul magvir morrub osmame pintae
pruser quealb quehem queshu quevir ulmala araspi cyrrac;
run;
/* The observations are sorted by their ident value.
*/
proc sort data=wood;
by ident;
run;
/* The cluster procedure is for hierarchical clustering.
* The method option specifies the cluster distance formula to use.
* The outtree option saves the results.
*/
proc cluster data=wood method=complete outtree=clust1;
var carcar corflo faggra ileopa liqsty maggra nyssyl ostvir oxyarb
pingla quenig quemic symtin;
id ident;
run;
/* The tree procedure generates a dendrogram of the heirarchical
* clustering results and saves cluster label assignments if the
* nclusters option is also specified.
*/
proc tree data=clust1 horizontal nclusters=6 out=clust2;
id ident;
run;
/* The data are sorted by their ident value.
*/
proc sort data=clust2;
by ident;
run;
/* The results from clust2 are printed.
*/
proc print data=clust2;
run;
/* This step combines the original wood data set with
* the results of clust2, which allows the ANOVA statistics
* to be calculated in the following glm procedure.
*/
data combine;
merge wood clust2;
by ident;
run;
/* The glm procedure views the cluster labels as ANOVA groups and
* reports several statistics to assess variation between clusters
* relative to variation within clusters.
* The mean for each cluster is also reported.
*/
proc glm data=combine;
class cluster;
model carcar corflo faggra ileopa liqsty maggra nyssyl ostvir oxyarb
pingla quenig quemic symtin = cluster;
means cluster;
run;
Performing a cluster analysis
To perform cluster analysis:
- Open the ‘wood’ data set in a new worksheet.
- Stat > Multivariate > Cluster Observations
- Highlight and select the variables to use in the clustering. For this example, the following variables are selected (13 total): carcar corflo faggra ileopa liqsty maggra nyssyl ostvir oxyarb pingla quenig quemic symtin
- Choose Complete as the Linkage and Euclidean as the Distance.
- Choose Show dendrogram, and under Customize, choose Distance for Y Axis.
- Choose OK, and OK again. The results, along with the dendrogram, are shown in the session window.
Dendrograms (Tree Diagrams)
The results of cluster analysis are best summarized using a dendrogram. In a dendrogram, distance is plotted on one axis, while the sample units are given on the remaining axis. The tree shows how the sample units are combined into clusters, the height of each branching point corresponding to the distance at which two clusters are joined.
In looking at the cluster history section of the SAS (or Minitab) output, we see that the Euclidean distance between sites 33 and 51 was smaller than between any other pair of sites (clusters). Therefore, this pair of sites were clustered first in the tree diagram. Following the clustering of these two sites, there are a total of n - 1 = 71 clusters, and so, the cluster formed by sites 33 and 51 is designated "CL71". Note that the numerical values of the distances in SAS and in Minitab are different because SAS shows a 'normalized' distance. We are interested in the relative ranking for cluster formation, rather than the absolute value of the distance anyhow.
The Euclidean distance between sites 15 and 23 was smaller than between any other pair of the 70 unclustered sites or the distance between any of those sites and CL71. Therefore, this pair of sites were clustered second. Its designation is "CL70".
In the seventh step of the algorithm, the distance between site 8 and cluster CL67 was smaller than the distance between any pair of unclustered sites and the distances between those sites and the existing clusters. Therefore, site 8 was joined to CL67 to form the cluster of 3 sites designated as CL65.
The clustering algorithm is completed when clusters CL2 and CL5 are joined.
The plot below is generated by Minitab. In SAS the diagram is horizontal. The color scheme depends on how many clusters are created (discussed later).
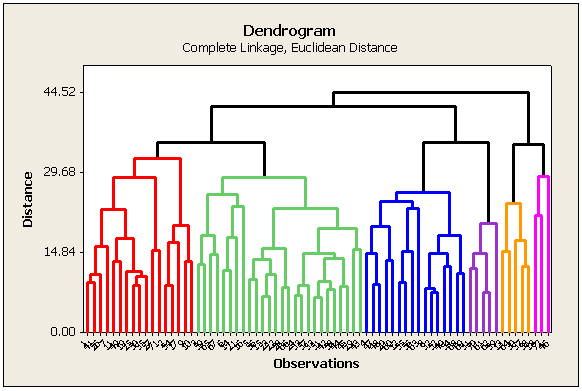
What do you do with the information in this tree diagram?
We decide the optimum number of clusters and which clustering technique to use. We adapted the wood1.sas program to specify the use of the other clustering techniques. Here are links to these program changes. In Minitab also you may select other options instead of a single linkage from the appropriate box.
| File Name | Description of Data |
|---|---|
| wood1.sas | specifies complete linkage |
| wood2.sas | is identical, except that it uses average linkage |
| wood3.sas | uses the centroid method |
| wood4.sas | uses the simple linkage |
As we run each of these programs we must remember to keep in mind that our goal is a good description of the data.
Applying the Cluster Analysis Process
First, we compare the results of the different clustering algorithms. Note that clusters containing one or only a few members are undesirable, as that will give rise to a large number of clusters, defeating the purpose of the whole analysis. That is not to say that we can never have a cluster with a single member! In fact, if that happens, we need to investigate the reason. It may indicate that the single-item cluster is completely different from the other members of the sample and is best left alone.
To arrive at the optimum number of clusters we may follow this simple guideline. Select the number of clusters that have been identified by each method. This is accomplished by finding a breakpoint (distance) below which further branching is ignored. In practice, this is not necessarily straightforward. You will need to try a number of different cut points to see which is more decisive. Here are the results of this type of partitioning using the different clustering algorithm methods on the Woodyard Hammock data. A dendrogram helps determine the breakpoint.
| Cluster Analysis | Linkage Type | Cluster Yield |
|---|---|---|
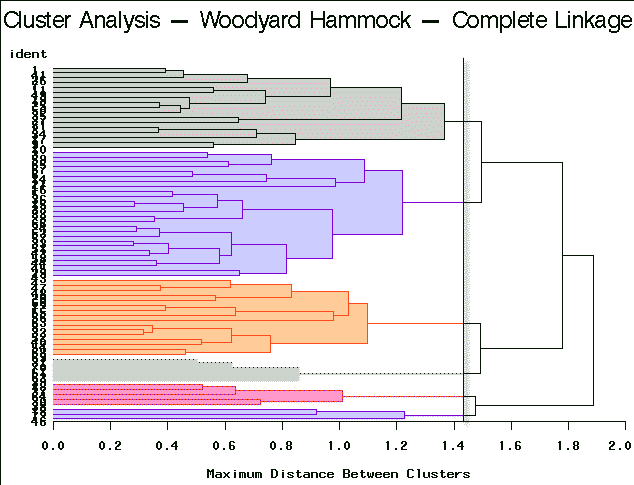 |
Complete Linkage | Partitioning into 6 clusters yields clusters of sizes 3, 5, 5, 16, 17, and 26. |
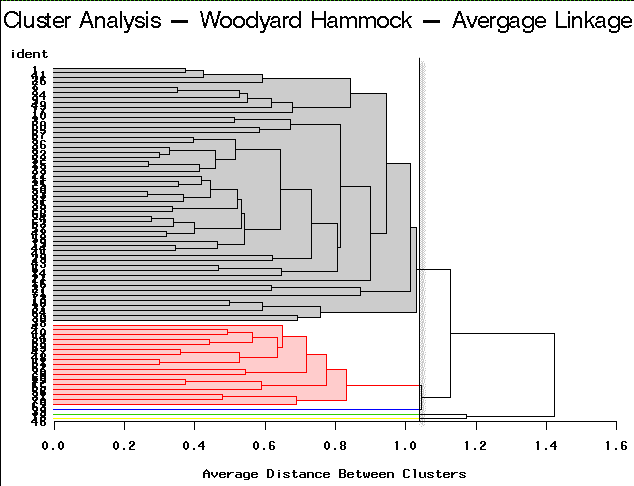 |
Average Linkage | Partitioning into 5 clusters would yield 3 clusters containing only a single site each. |
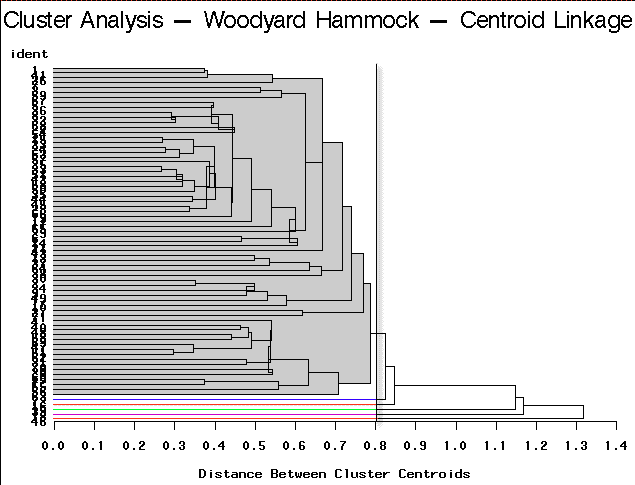 |
Centroid Linkage | Partitioning into 6 clusters would yield 5 clusters containing only a single site each. |
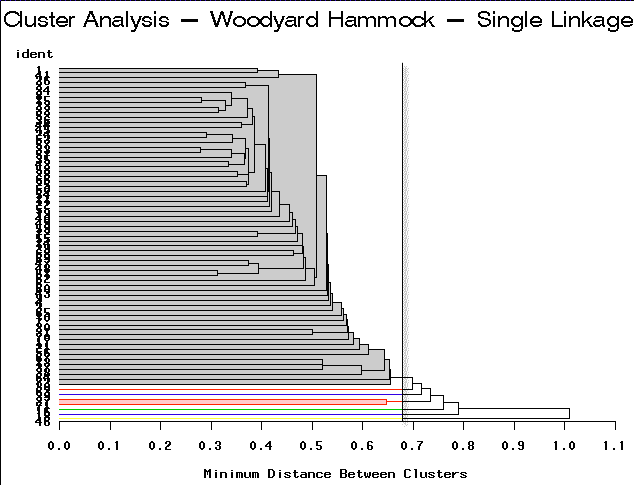 |
Single Linkage | Partitioning into 7 clusters would yield 6 clusters containing only 1-2 sites each. |
For this example, complete linkage yields the most satisfactory result.
For your convenience, the following screenshots demonstrate how alternative clustering procedures may be done in Minitab.
14.6 - Cluster Description
14.6 - Cluster DescriptionThe next step of cluster analysis is to describe the identified clusters.
The SAS program shows how this is implemented.
Download the SAS Program here: wood1.sas
Notice that in the cluster procedure, we created a new SAS dataset called clust1.
- This contains the information required by the tree procedure to draw the tree diagram.
In the tree procedure, we chose to investigate 6 clusters with ncluster=6.
- A new SAS dataset called clust2 is output with the id numbers of each site and the cluster that site belongs stored in a new variable called a cluster.
- We need to merge this back with the original data to describe the characteristics of each of the 6 clusters.
Now an Analysis of Variance for each species is carried out with a class statement for the grouping variable, cluster.
- We also include the means statement to get the cluster means.
Performing a cluster analysis, part 2
To perform cluster analysis with follow-up ANOVA on clusters:
- Open the ‘wood’ data set in a new worksheet.
- Stat > Multivariate > Cluster Observations
- Highlight and select the variables to use in the clustering. For this example, the following variables are selected (13 total): carcar, corflo, faggra, ileopa, liqsty, maggra, nyssyl, ostvir, oxyarb, pingla, quenig, quemic, symtin.
- Choose Complete as the Linkage and Euclidean as the Distance.
- Choose Show dendrogram, and under Customize, choose Distance for Y-Axis.
- Under Storage, enter c34 (or the name of any blank column in the worksheet) in the Cluster membership column.
- Choose OK, and OK again. In addition to the session window results, the cluster assignments are stored in the c34 column. We relabel this column as ‘cluster’ for the steps below.
- Stat > ANOVA > One-way
- Highlight and select any one of the variables used in the original clustering (in this example, we use carcar) to move it to the Response window.
- Highlight and select cluster to move it to the Factor window.
- Choose OK. The results, including the F statistic, are shown in the session window.
Analysis
We perform an analysis of variance for each of the tree species, comparing the means of the species across clusters. The Bonferroni method is applied to control the experiment-wise error rate. This means that we will reject the null hypothesis of equal means among clusters at level \(\alpha\) if the p-value is less than \(\alpha/ p\). Here, \(p = 13\) so for an \(\alpha = 0.05\) level test, we reject the null hypothesis of equality of cluster means if the p-value is less than \(0.05/13\) or \(0.003846\).
Here is the output for the species carcar.
| Pr > F | |||||
|---|---|---|---|---|---|
| Model | 5 | 4340.834339 | 868.166868 | 62.94 | < 0.0001 |
| Error | 66 | 910.443439 | 13.794598 | ||
| Corrected Total | 71 | 5251.277778 | |||
| R-Square | Coeff Var | Root MSE | carcar Mean |
|---|---|---|---|
| 0.826624 | 44.71836 | 3.714108 | 8.305556 |
| Source | DF | Type I SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| CLUSTER | 5 | 4340.834339 | 868.166868 | 62.94 | < 0.0001 |
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| CLUSTER | 5 | 4340.834339 | 868.166868 | 62.94 | < 0.0001 |
We collected the results of the individual species ANOVAs in the table below. The species names in boldface indicate significant results suggesting that there was significant variation among the clusters for that particular species.
| Code | Species | F | p-value |
|---|---|---|---|
| carcar | Ironwood | 62.94 | < 0.0001 |
| corflo | Dogwood | 1.55 | 0.1870 |
| faggra | Beech | 7.11 | < 0.0001 |
| ileopa | Holly | 3.42 | 0.0082 |
| liqsty | Sweetgum | 5.87 | 0.0002 |
| maggra | Magnolia | 3.97 | 0.0033 |
| nyssyl | Blackgum | 1.66 | 0.1567 |
| ostvir | Blue Beech | 17.70 | < 0.0001 |
| oxyarb | Sourwood | 1.42 | 0.2294 |
| pingla | Spruce Pine | 0.43 | 0.8244 |
| quenig | Water Oak | 2.23 | 0.0612 |
| quemic | Swamp Chestnut Oak | 4.12 | 0.0026 |
| symtin | Horse Sugar | 75.57 | < 0.0001 |
d.f. = 5, 66
The results indicate that there are significant differences among clusters for ironwood, beech, sweetgum, magnolia, blue beech, swamp chestnut oak, and horse sugar.
Next, SAS computed the cluster means for each of the species. Here is a sample of the output with a couple of significant species highlighted.

We collected the cluster means for each of the significant species indicated above and placed the values in the table below:
| Code | Cluster | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| carcar | 3.8 | 24.4 | 18.5 | 1.2 | 8.2 | 6.0 |
| faggra | 11.4 | 6.4 | 5.9 | 5.9 | 8.6 | 2.7 |
| liqsty | 7.2 | 17.4 | 6.4 | 6.8 | 6.6 | 18.0 |
| maggra | 5.3 | 3.8 | 2.8 | 3.2 | 4.6 | 0.7 |
| ostvir | 4.3 | 2.8 | 2.9 | 13.8 | 3.6 | 14.0 |
| quemic | 5.3 | 5.2 | 9.4 | 4.1 | 7.0 | 2.3 |
| symtin | 0.9 | 0.0 | 0.7 | 2.0 | 18.0 | 20.0 |
The boldface values highlight the clusters where each species is abundant. For example, carcar (ironwood) is abundant in clusters 2 and 3. This operation is carried out across the rows of the table.
Each cluster is then characterized by the species that are highlighted in its column. For example, cluster 1 is characterized by a high abundance of faggra, or beech trees. This operation is carried out across the columns of the table.
In summary, we find:
- Cluster 1: primarily Beech (faggra)
- Cluster 2: Ironwood (carcar) and Sweetgum (liqsty)
- Cluster 3: Ironwood (carcar) and Swamp Chestnut Oak(quemic)
- Cluster 4: primarily Blue Beech (ostvir)
- Cluster 5: Beech (faggra), Swamp Chestnut Oak(quemic), and Horse Sugar(symtin)
- Cluster 6: Sweetgum (liqsty), Blue Beech (ostvir) and Horse Sugar(symtin)
It is also useful to summarize the results in the cluster diagram:
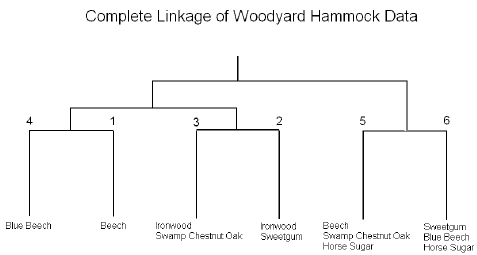
We can see that the two ironwood clusters (2 and 3) are joined. Ironwood is an understory species that tend to be found in wet regions that may be frequently flooded. Cluster 2 also contains sweetgum, an overstory species found in disturbed habitats, while cluster 3 contains swamp chestnut oak, an overstory species characteristic of undisturbed habitats.
Clusters 5 and 6 both contain horse sugar, an understory species characteristic of light gaps in the forest. Cluster 5 also contains beech and swamp chestnut oak, two overstory species characteristic of undisturbed habitats. These are likely to be saplings of the two species growing in the horse sugar light gaps. Cluster 6 also contains blue beech, an understory species similar to ironwood, but characteristic of uplands.
Cluster 4 is dominated by blue beech, an understory species characteristic of uplands
Cluster 1 is dominated by beech, an overstory species most abundant in undisturbed habitats.
From the above description, you can see that a meaningful interpretation of the results of cluster analysis is best obtained using subject-matter knowledge.
14.7 - Ward’s Method
14.7 - Ward’s MethodThis is an alternative approach for performing cluster analysis. Basically, it looks at cluster analysis as an analysis of variance problem instead of using distance metrics or measures of association.
This method involves an agglomerative clustering algorithm. It will start out at the leaves and work its way to the trunk, so to speak. It looks for groups of leaves that form into branches, the branches into limbs, and eventually into the trunk. Ward's method starts out with n clusters of size 1 and continues until all the observations are included in one cluster.
This method is most appropriate for quantitative variables and not binary variables.
Based on the notion that clusters of multivariate observations should be approximately elliptical in shape, we assume that the data from each of the clusters have been realized in a multivariate distribution. Therefore, it would follow that they would fall into an elliptical shape when plotted in a p-dimensional scatter plot.
Let \(X _ { i j k }\) denote the value for variable k in observation j belonging to cluster i.
Furthermore, we define:
We sum over all variables and all of the units within each cluster. We compare individual observations for each variable against the cluster means for that variable.
The total sums of squares are defined the same as always. Here we compare the individual observations for each variable against the grand mean for that variable.
This \(r^{2}\) value is interpreted as the proportion of variation explained by a particular clustering of the observations.
- Error Sum of Squares: \(ESS = \sum_{i}\sum_{j}\sum_{k}|X_{ijk} - \bar{x}_{i\cdot k}|^2\)
- Total Sum of Squares: \(TSS = \sum_{i}\sum_{j}\sum_{k}|X_{ijk} - \bar{x}_{\cdot \cdot k}|^2\)
- R-Square: \(r^2 = \frac{\text{TSS-ESS}}{\text{TSS}}\)
Using Ward's Method we start out with all sample units in n clusters of size 1 each. In the first step of the algorithm, n - 1 clusters are formed, one of size two and the remaining of size 1. The error sum of squares and \(r^{2}\) values are then computed. The pair of sample units that yield the smallest error sum of squares, or equivalently, the largest \(r^{2}\) value will form the first cluster. Then, in the second step of the algorithm, n - 2 clusters are formed from that n - 1 clusters defined in step 2. These may include two clusters of size 2 or a single cluster of size 3 including the two items clustered in step 1. Again, the value of \(r^{2}\) is maximized. Thus, at each step of the algorithm, clusters or observations are combined in such a way as to minimize the results of error from the squares or alternatively maximize the \(r^{2}\) value. The algorithm stops when all sample units are combined into a single large cluster of size n.
Example 14-3: Woodyard Hammock Data (Ward's Method)
We will take a look at the implementation of Ward's Method using the SAS program below. Minitab implementation is also similar. Minitab is not shown separately.
Download the SAS Program here: wood5.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Cluster Analysis - Woodyard Hammock - Ward's Method";
/* After reading in the data, an ident variable is created as the
* row number for each observation. This is neeed for the clustering algorithm.
* The drop statement removes several variables not used for this analysis.
*/
data wood;
infile 'D:\Statistics\STAT 505\data\wood.csv' firstobs=2 delimiter=',';
input x y acerub carcar carcor cargla cercan corflo faggra frapen
ileopa liqsty lirtul maggra magvir morrub nyssyl osmame ostvir
oxyarb pingla pintae pruser quealb quehem quenig quemic queshu quevir
symtin ulmala araspi cyrrac;
ident=_n_;
drop acerub carcor cargla cercan frapen lirtul magvir morrub osmame pintae
pruser quealb quehem queshu quevir ulmala araspi cyrrac;
run;
/* The observations are sorted by their ident value.
*/
proc sort data=wood;
by ident;
run;
/* The cluster procedure is for hierarchical clustering.
* The method option specifies the cluster distance formula to use.
* The outtree option saves the results.
*/
proc cluster data=wood method=ward outtree=clust1;
var carcar corflo faggra ileopa liqsty maggra nyssyl ostvir oxyarb
pingla quenig quemic symtin;
id ident;
run;
/* The tree procedure generates a dendrogram of the heirarchical
* clustering results and saves cluster label assignments if the
* nclusters option is also specified.
*/
proc tree data=clust1 horizontal nclusters=6 out=clust2;
id ident;
run;
/* The data are sorted by their ident value.
*/
proc sort data=clust2;
by ident;
run;
/* This step combines the original wood data set with
* the results of clust2, which allows the ANOVA statistics
* to be calculated in the following glm procedure.
*/
data combine;
merge wood clust2;
by ident;
run;
/* The glm procedure views the cluster labels as ANOVA groups and
* reports several statistics to assess variation between clusters
* relative to variation within clusters.
* The mean for each cluster is also reported.
*/
proc glm data=combine;
class cluster;
model carcar corflo faggra ileopa liqsty maggra nyssyl ostvir oxyarb
pingla quenig quemic symtin = cluster;
means cluster;
run;
As you can see, this program is very similar to the previous program, (wood1.sas), that was discussed earlier in this lesson. The only difference is that we have specified that method=ward in the cluster procedure as highlighted above. The tree procedure is used to draw the tree diagram shown below, as well as to assign cluster identifications. Here we will look at four clusters.
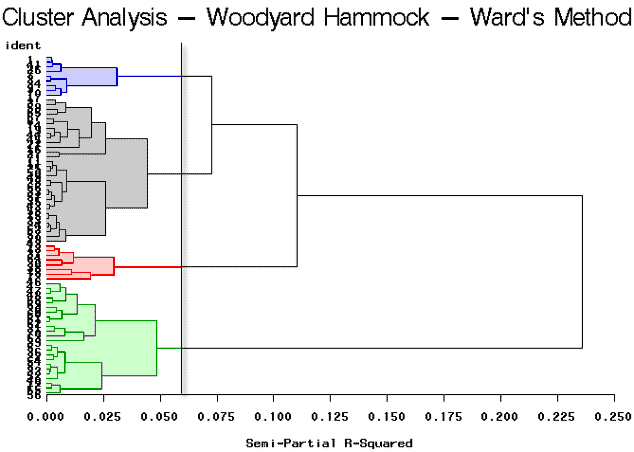
The break in the plot shows four highlighted clusters. It looks as though there are two very well-defined clusters because it shows a large break between the first and second branches of the tree. The partitioning results in 4 clusters yielding clusters of sizes 31, 24, 9, and 8.
Referring back to the SAS output, the results of the ANOVAs are copied here for discussion.
| Code | Species | F | p-value |
|---|---|---|---|
| carcar | Ironwood | 67.42 | < 0.0001 |
| corflo | Dogwood | 2.31 | 0.0837 |
| faggra | Beech | 7.13 | 0.0003 |
| ileopa | Holly | 5.38 | 0.0022 |
| liqsty | Sweetgum | 0.76 | 0.5188 |
| maggra | Magnolia | 2.75 | 0.0494 |
| nyssyl | Blackgum | 1.36 | 0.2627 |
| ostvir | Blue Beech | 32.91 | < 0.0001 |
| oxyarb | Sourwood | 3.15 | 0.0304 |
| pingla | Spruce Pine | 1.03 | 0.3839 |
| quenig | Water Oak | 2.39 | 0.0759 |
| quemic | Swamp Chestnut Oak | 3.44 | 0.0216 |
| symtin | Horse Sugar | 120.95 | < 0.0001 |
d.f. = 3, 68
We boldfaced the species whose F-values, using a Bonferroni correction, show significance. These include Ironwood, Beech, Holly, Blue Beech, and Horse Sugar.
Next, we look at the cluster Means for these significant species:
| Code | Cluster | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| carcar | 2.8 | 18.5 | 1.0 | 7.4 |
| faggra | 10.6 | 6.0 | 5.9 | 6.4 |
| ileopa | 7.5 | 4.3 | 12.3 | 7.9 |
| ostvir | 5.4 | 3.1 | 18.3 | 7.5 |
| symtin | 1.3 | 0.7 | 1.4 | 18.8 |
Again, we boldfaced the values that show an abundance of that species within the different clusters.
- Cluster 1: Beech (faggra): Canopy species typical of old-growth forests.
- Cluster 2: Ironwood (carcar): Understory species that favors wet habitats.
- Cluster 3: Holly (ileopa) and Blue Beech (ostvir): Understory species that favor dry habitats.
- Cluster 4: Horse Sugar(symtin): Understory species typically found in disturbed habitats.
Note! This interpretation is cleaner than the interpretation obtained earlier from the complete linkage method. This suggests that Ward's method may be preferred for the current data.
The results are summarized in the following dendrogram:
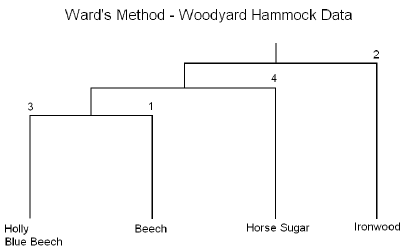
In summary, this method is performed in essentially the same manner as the previous method the only difference is that the cluster analysis is based on the Analysis of Variance instead of distances.
14.8 - K-Means Procedure
14.8 - K-Means ProcedureThis final method that we would like to examine is a non-hierarchical approach. This method was presented by MacQueen (1967) in the Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability.
One advantage of this method is that we do not have to calculate the distance measures between all pairs of subjects. Therefore, this procedure seems much more efficient or practical when you have very large datasets.
Under this procedure, you need to pre-specify how many clusters to consider. The clusters in this procedure do not form a tree. There are two approaches to carrying out the K-Means procedure. The approaches vary as to how the procedure begins the partitioning. The first approach is to do this randomly, which is to start out with a random partitioning of subjects into groups and go from there. The alternative is to start with an additional set of starting points to form the centers of the clusters. The random nature of the first approach avoids bias.
Once this decision has been made, here is an overview of the process:
- Step 1: Partition the items into K initial clusters.
- Step 2: Scan through the list of n items, assigning each item to the cluster whose centroid (mean) is closest. Each time an item is reassigned, we recalculate the cluster mean or centroid for the cluster receiving that item and the cluster losing that item.
- Step 3: Repeat Step 2 over and over again until no more reassignments are made.
Let's look at a simple example in order to see how this works. Here is an example where we have four items and two variables:
| Item | \(X_{1}\) | \(X_{2}\) |
|---|---|---|
| A | 7 | 9 |
| B | 3 | 3 |
| C | 4 | 1 |
| D | 3 | 8 |
Suppose that we initially decide to partition the items into two clusters (A, B) and (C, D). The cluster centroids, or the mean of all the variables within the cluster, are as follows:
| Cluster | \(\overline { x } _ { 1 }\) | \(\overline { x } _ { 2 }\) |
|---|---|---|
| (A, B) | \(\dfrac { 7 + 3 } { 2 } = 5\) | \(\dfrac { 9 + 3 } { 2 } = 6\) |
| (C, D) | \(\dfrac{4+3}{2} = 3.5\) | \(\dfrac { 1 + 8 } { 2 } = 4.5\) |
For example, the mean of the first variable for cluster (A, B) is 5.
Next, we calculate the distances between item A and the centroids of clusters (A, B) and (C, D).
| Cluster | Distance to A |
|---|---|
| (A, B) | \(\sqrt { ( 7 - 5 ) ^ { 2 } + ( 9 - 6 ) ^ { 2 } } = \sqrt { 13 }\) |
| (C, D) | \(\sqrt { ( 7 - 3.5 ) ^ { 2 } + ( 9 - 4.5 ) ^ { 2 } } = \sqrt { 32.5 }\) |
This is the Euclidean distance between A and each of the cluster centroids. We see that item A is closer to cluster (A, B) than cluster (C, D). Therefore, we are going to leave item A in cluster (A, B) and no change is made at this point.
Next, we will look at the distance between item B and the centroids of clusters (A, B) and (C, D).
| Cluster | Distance to B |
|---|---|
| (A, B) | \(\sqrt { ( 3 - 5 ) ^ { 2 } + ( 3 - 6 ) ^ { 2 } } = \sqrt { 13 }\) |
| (C, D) | \(\sqrt { ( 3 - 3.5 ) ^ { 2 } + ( 3 - 4.5 ) ^ { 2 } } = \sqrt { 2.5 }\) |
Here, we see that item B is closer to cluster (C, D) than cluster (A, B). Therefore, item B will be reassigned, resulting in the new clusters (A) and (B, C, D).
The centroids of the new clusters are calculated as:
| Cluster | \(\overline { x } _ { 1 }\) | \(\overline { x } _ { 2 }\) |
|---|---|---|
| (A) | 7 | 9 |
| (B, C, D) | \(\frac { 3 + 4 + 3 } { 3 } = 3 . \overline { 3 }\) | \(\frac { 3 + 1 + 8 } { 3 } = 4\) |
Next, we will calculate the distance between the items and each of the clusters (A) and (B, C, D).
| Cluster | C | D | A | B |
|---|---|---|---|---|
| (A) | \(\sqrt {73 }\) | \(\sqrt { 17 }\) | 0 | \(\sqrt { 52 }\) |
| (B, C, D) | \(\sqrt { 9 . \overline { 4 } }\) | \(\sqrt { 16 . \overline { 1 } }\) | \(\sqrt { 38 . \overline { 4 } }\) | \(\sqrt { 1 . \overline { 1 } }\) |
It turns out that since all four items are closer to their current cluster centroids, no further reassignments are required.
We must note, however, that the results of the K-means procedure can be sensitive to the initial assignment of clusters.
For example, suppose the items had initially been assigned to the clusters (A, C) and (B, D). Then the cluster centroids would be calculated as follows:
| Cluster | \(\overline { x } _ { 1 }\) | \(\overline { x } _ { 2 }\) |
|---|---|---|
| (A, C) | \(\dfrac { 7 + 4 } { 2 } = 5.5\) | \(\dfrac { 9 + 1 } { 2 } = 5\) |
| (B, D) | \(\dfrac{3+3}{2} = 3\) | \(\dfrac { 3 + 8 } { 2 } = 5.5\) |
From here we can find that the distances between the items and the cluster centroids are:
| Cluster | A | B | C | D |
|---|---|---|---|---|
| (A, C) | \(\sqrt {18.25}\) | \(\sqrt {10.25 }\) | \(\sqrt {18.25}\) | \(\sqrt {15.25 }\) |
| (B, D) | \(\sqrt {28.25}\) | \(\sqrt {6.25 }\) | \(\sqrt {21.25 }\) | \(\sqrt {6.25}\) |
Question
If this is the case, then which result should be used as our summary?
We can compute the sum of squared distances between the items and their cluster centroid. For our first clustering scheme for clusters (A) and (B, C, D), we had the following distances to cluster centroids:
| Cluster | C | D | A | B |
|---|---|---|---|---|
| (A) | \(\sqrt {73 }\) | \(\sqrt { 17 }\) | 0 | \(\sqrt { 52 }\) |
| (B, C, D) | \(\sqrt { 9 . \overline { 4 } }\) | \(\sqrt { 16 . \overline { 1 } }\) | \(\sqrt { 38 . \overline { 4 } }\) | \(\sqrt { 1 . \overline { 1 } }\) |
So, the sum of squared distances is:
\(9.\bar{4} + 16.\bar{1} + 0 + 1.\bar{1} = 26.\bar{6}\)
For clusters (A, C) and (B, D), we had the following distances to cluster centroids:
| Cluster | A | B | C | D |
|---|---|---|---|---|
| (A, C) | \(\sqrt {18.25 }\) | \(\sqrt {10.25 }\) | \(\sqrt {18.25 }\) | \(\sqrt {15.25 }\) |
| (B, D) | \(\sqrt {28.25 }\) | \(\sqrt {6.25 }\) | \(\sqrt {21.25 }\) | \(\sqrt {6.25 }\) |
So, the sum of squared distances is:
\(18.25 + 6.25 + 18.25 + 6.25 = 49. 0\)
We would conclude that since \(26.\bar{6} < 49.0\), this would suggest that the first clustering scheme is better and partition the items into the clusters (A) and (B, C, D).
In practice, several initial clusters should be tried and compared to find the best results. A question arises, however, how should we define the initial clusters?
14.9 - Defining Initial Clusters
14.9 - Defining Initial ClustersNow that you have a good idea of what is going to happen, we need to go back to our original question for this method... How should we define the initial clusters? Again, there are two main approaches that are taken to define the initial clusters.
1st Approach: Random assignment
The first approach is to assign the clusters randomly. This does not seem like it would be a very efficient approach. The main reason to take this approach would be to avoid any bias in this process.
2nd Approach: Leader Algorithm
The second approach is to use a Leader Algorithm. (Hartigan, J.A., 1975, Clustering Algorithms). This involves the following procedure:
- Step 1. Select the first item from the list. This item forms the centroid of the initial cluster.
- Step 2. Search through the subsequent items until an item is found that is at least distance δ away from any previously defined cluster centroid. This item will form the centroid of the next cluster.
- Step 3: Step 2 is repeated until all K cluster centroids are obtained or no further items can be assigned.
- Step 4: The initial clusters are obtained by assigning items to the nearest cluster centroids.
The following video illustrates this procedure for k = 4 clusters and p = 2 variables plotted in a scatter plot:
Example 14-5: Woodyard Hammock Data (Initial Clusters)
Now, let's take a look at each of these options, in turn, using our Woodyard Hammock dataset.
We first must determine:
- The number of clusters K
- The radius \(δ\) for the leader algorithm.
In some applications, the theory specific to the discipline may suggest reasonable values for K. In general, however, there is no prior knowledge that can be applied to find K. Our approach is to apply the following procedure for various values of K. For each K, we obtain a description of the resulting clusters. The value of K is then selected to yield the most meaningful description. We wish to select K large enough so that the composition of the individual clusters is uniform, but not so large as to yield too complex a description for the resulting clusters.
Here, we shall take K = 4 and use the random assignment approach to find a reasonable value for \(δ\).
This random approach is implemented in SAS using the following program below.
Download the SAS Program here: wood6.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Cluster Analysis - Woodyard Hammock - K-Means";
/* After reading in the data, an ident variable is created as the
* row number for each observation. This is neeed for the clustering algorithm.
* The drop statement removes several variables not used for this analysis.
*/
data wood;
infile 'D:\Statistics\STAT 505\data\wood.csv' firstobs=2 delimiter=',';
input x y acerub carcar carcor cargla cercan corflo faggra frapen
ileopa liqsty lirtul maggra magvir morrub nyssyl osmame ostvir
oxyarb pingla pintae pruser quealb quehem quenig quemic queshu quevir
symtin ulmala araspi cyrrac;
ident=_n_;
drop acerub carcor cargla cercan frapen lirtul magvir morrub osmame pintae
pruser quealb quehem queshu quevir ulmala araspi cyrrac;
run;
/* The observations are sorted by their ident value.
*/
proc sort data=wood;
by ident;
run;
/* The fastclus is a non-hierarchical procedure.
* The maxclusters option is the number it works with
* throughout the algorithm. The replace option specifies
* the way seeds are replaced.
*/
proc fastclus data=wood maxclusters=4 replace=random;
var carcar corflo faggra ileopa liqsty maggra nyssyl ostvir oxyarb
pingla quenig quemic symtin;
id ident;
run;
We use the fastclus procedure, which stands for fast cluster analysis. This is designed specifically to develop results quickly, especially with very large datasets. Remember, unlike the previous cluster analysis methods, we will not get a tree diagram out of this procedure.
We need to first specify the number of clusters that we want to include. In this case, we ask for four clusters. Then, we set replace=random, indicating the initial cluster of centroids will be randomly selected from the study subjects (sites).
Perform a cluster analysis (kmeans)
To perform k-means cluster analysis:
- Open the ‘wood’ data set in a new worksheet.
- Stat > Multivariate > Cluster K-means
- Highlight and select the variables to use in the clustering. For this example, the following variables are selected (13 total): carcar corflo faggra ileopa liqsty maggra nyssyl ostvir oxyarb pingla quenig quemic symtin
- Choose 4 as the number of clusters.
- In Storage, enter c35 (or the name of any blank column in the worksheet) in Cluster membership column.
- Choose OK, and OK again. In addition to the session window results, the cluster assignments are stored in the c35 column, which can be used for any subsequent ANOVA analysis.
When you run this program, you will always get different results because a different random set of subjects is selected each time.
The first part of the output gives the initial cluster centers. SAS picks four sites at random and lists how many species of each tree are at each site.
The procedure works iteratively until no reassignments can be obtained. The following table was copied from the SAS output for discussion purposes.
| Cluster | Maximum Point to Centroid Distance | Nearest Cluster | Distance to Closest Cluster |
|---|---|---|---|
| 1 | 21.1973 | 3 | 16.5910 |
| 2 | 20.2998 | 3 | 13.0501 |
| 3 | 22.1861 | 2 | 13.0501 |
| 4 | 23.1866 | 3 | 15.8186 |
In this case, we see that cluster 3 is the nearest neighboring cluster to cluster 1 and the distance between those two clusters is 16.591.
To set the delta for the leader algorithm, we want to pay attention to the maximum distances between the cluster centroids and the furthest site in that cluster. We can see that all of the maximum distances exceed 20. Based on these results, we set the radius \(δ = 20\).
Now, we can turn to the SAS program below where this radius \(δ\) value is used to run the Leader Algorithmic approach.
Here is the SAS program modified to accommodate these changes:
Download the SAS Program here: wood7.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Cluster Analysis - Woodyard Hammock - K-Means";
/* After reading in the data, an ident variable is created as the
* row number for each observation. This is neeed for the clustering algorithm.
* The drop statement removes several variables not used for this analysis.
*/
data wood;
infile 'D:\Statistics\STAT 505\data\wood.csv' firstobs=2 delimiter=',';
input x y acerub carcar carcor cargla cercan corflo faggra frapen
ileopa liqsty lirtul maggra magvir morrub nyssyl osmame ostvir
oxyarb pingla pintae pruser quealb quehem quenig quemic queshu quevir
symtin ulmala araspi cyrrac;
ident=_n_;
drop acerub carcor cargla cercan frapen lirtul magvir morrub osmame pintae
pruser quealb quehem queshu quevir ulmala araspi cyrrac;
run;
/* The observations are sorted by their ident value.
*/
proc sort data=wood;
by ident;
run;
/* The fastclus is a non-hierarchical procedure.
* The maxclusters option is the number it works with
* throughout the algorithm. The radius option specifies
* the minimum distance between new seeds.
* The maxiter option specifies the number of iterations.
*/
proc fastclus data=wood maxclusters=4 radius=20 maxiter=100 out=clust;
var carcar corflo faggra ileopa liqsty maggra nyssyl ostvir oxyarb
pingla quenig quemic symtin;
id ident;
run;
The fastclus procedure is used again, only this time with the leader algorithm options specified.
We set the maximum number of clusters to four and also set the radius to equal 20, the delta value that we decided on earlier.
Again, the output produces the initial cluster of centroids. Given the first site, it will go down the list of the sites until it finds another site that is at least 20 away from this first point. The first one it finds forms the second cluster centroid. Then it goes down the list until it finds another site that is at least 20 away from the first two to form the third cluster centroid. Finally, the fourth cluster is formed by searching until it finds a site that is at least 20 away from the first three.
SAS also provides an iteration history showing what happens during each iteration of the algorithm. The algorithm stops after five iterations, showing the changes in the location of the centroids. In other words, convergence was achieved after 5 iterations.
Next, the SAS output provides a cluster summary that gives the number of sites in each cluster. It also tells you which cluster is closest. From this, it seems that Cluster 1 is in the middle because three of the clusters (2,3, and 4) are closest to Cluster 1 and not the other clusters. The distances between the cluster centroids and their nearest neighboring clusters are reported, i.e., Cluster 1 is 14.3 away from Cluster 4. The SAS output from all four clusters is in the table below:
| Cluster | Size | Nearest Neighbor | Distance |
|---|---|---|---|
| 1 | 28 | 4 | 14.3126 |
| 2 | 9 | 1 | 17.6003 |
| 3 | 18 | 1 | 19.3971 |
| 4 | 17 | 1 | 14.3126 |
In comparing these spacings with the spacing we found earlier, you will notice that these clusters are more widely spaced than the previously defined clusters.
The output of fastclus also gives the results of individual ANOVAs for each species. However, only the \(r^{2}\) values for each ANOVAs are presented. The \(r^{2}\) values are computed, as usual, by dividing the model sum of squares by the total sum of squares. These are summarized in the following table:
| Code | Species | \(\boldsymbol{r^{2}}\) | \(\boldsymbol{r ^ { 2 } / \left( 1 - r ^ { 2 } \right)}\) | F |
|---|---|---|---|---|
| carcar | Ironwood | 0.785 | 3.685 | 82.93 |
| corflo | Dogwood | 0.073 | 0.079 | 1.79 |
| faggra | Beech | 0.299 | 0.427 | 9.67 |
| ileopa | Holly | 0.367 | 0.579 | 13.14 |
| liqsty | Sweetgum | 0.110 | 0.123 | 2.80 |
| maggra | Magnolia | 0.199 | 0.249 | 5.64 |
| nyssyl | Blackgum | 0.124 | 0.142 | 3.21 |
| ostvir | Blue Beech | 0.581 | 1.387 | 31.44 |
| oxyarb | Sourwood | 0.110 | 0.124 | 2.81 |
| pingla | Spruce Pine | 0.033 | 0.034 | 0.76 |
| quenig | Water Oak | 0.119 | 0.135 | 3.07 |
| quemic | Swamp Chestnut Oak | 0.166 | 0.199 | 4.50 |
| symtin | Horse Sugar | 0.674 | 2.063 | 46.76 |
Given \(r^{2}\) , the F-statistic is:
\(F = \dfrac{r^2/(K-1)}{(1-r^2)/(n-K)}\)
where K-1 is the degrees of freedom between clusters and n-K is the degrees of freedom within clusters.
In our example, n = 72 and K = 4. If we take the ratio of \(r^{2}\) divided by 1-\(r^{2}\), multiply the result by 68, and divide by 3, we arrive at the F-values in the table.
Each of these F-values is tested at K - 1 = 3 and n - K = 68 degrees of freedom. Using the Bonferroni correction, the critical value for an \(α = 0.05\) level test is \(F_{3,68,0.05/13} = 4.90 \). Therefore, anything above 4.90 will be significant here. In this case, the species in boldface in the table above are the species where the F-value is above 4.90.
Let's look at the cluster means for the significant species identified above. The species and the species' means are listed in the table below. As before, the larger numbers within each row are boldfaced. As a result, you can see that ironwood is most abundant in Cluster 3, Beech is most abundant in Cluster 1, and so forth...
| Cluster | ||||
|---|---|---|---|---|
| Species | 1 | 2 | 3 | 4 |
| Ironwood | 4.1 | 7.2 | 21.2 | 2.1 |
| Beech | 11.1 | 6.1 | 5.7 | 6.2 |
| Holly | 5.5 | 5.9 | 4.4 | 13.2 |
| Magnolia | 5.3 | 3.3 | 2.8 | 3.0 |
| Blue Beech | 4.5 | 5.3 | 2.4 | 14.6 |
| Horse Sugar | 0.9 | 16.1 | 0.6 | 2.2 |
In looking down at the columns of the table, we can characterize the individual clusters:
- Cluster 1: Primarily Beech and Magnolia: These are the large canopy species typical of old-growth forests.
- Cluster 2: Primarily Horse Sugar: These are small understory species typical of small-scale disturbances (light gaps) in the forest.
- Cluster 3: Primarily Ironwood: This is an understory species typical of wet habitats.
- Cluster 4: Primarily Holly and Blue Beech: This is also an understory species typical of dry habitats.
14.10 - Summary
14.10 - SummaryIn this lesson we learned about:
- Methods for measuring distances or similarities between subjects
- Linkage methods for measuring the distances between clusters
- The difference between agglomerative and divisive clustering
- How to interpret tree diagrams and select how many clusters are of interest
- How to use individual ANOVAs and cluster means to describe cluster composition
- The definition of Ward's method
- The definition of the K-means method