Lesson 8: Multivariate Analysis of Variance (MANOVA)
Lesson 8: Multivariate Analysis of Variance (MANOVA)Overview
The Multivariate Analysis of Variance (MANOVA) is the multivariate analog of the Analysis of Variance (ANOVA) procedure used for univariate data. We will introduce the Multivariate Analysis of Variance with the Romano-British Pottery data example.
Pottery shards are collected from four sites in the British Isles:
- L: Llanedyrn
- C: Caldicot
- I: Isle Thorns
- A: Ashley Rails
Subsequently, we will use the first letter of the name to distinguish between the sites.
Each pottery sample was returned to the laboratory for chemical assay. In these assays the concentrations of five different chemicals were determined:
- Al: Aluminum
- Fe: Iron
- Mg: Magnesium
- Ca: Calcium
- Na: Sodium
We will abbreviate the chemical constituents with the chemical symbol in the examples that follow.
MANOVA will allow us to determine whether the chemical content of the pottery depends on the site where the pottery was obtained. If this is the case, then in Lesson 10, we will learn how to use the chemical content of a pottery sample of unknown origin to hopefully determine which site the sample came from.
Objectives
- Use SAS/Minitab to perform a multivariate analysis of variance;
- Draw appropriate conclusions from the results of a multivariate analysis of variance;
- Understand the Bonferroni method for assessing the significance of individual variables;
- Understand how to construct and interpret orthogonal contrasts among groups (treatments)
8.1 - The Univariate Approach: Analysis of Variance (ANOVA)
8.1 - The Univariate Approach: Analysis of Variance (ANOVA)In the univariate case, the data can often be arranged in a table as shown in the table below:
| 1 | 2 | \(\dots\) | g | ||
|---|---|---|---|---|---|
| Subjects | 1 | \(Y_{11}\) | \(Y_{21}\) | \(\dots\) | \(Y_{g_1}\) |
| 2 | \(Y_{12}\) | \(Y_{22}\) | \(\dots\) | \(Y_{g_2}\) | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | ||
| \(n_i\) | \(Y_{1n_1}\) | \(Y_{2n_2}\) | \(\dots\) | \(Y_{gn_g}\) | |
The columns correspond to the responses to g different treatments or from g different populations. And, the rows correspond to the subjects in each of these treatments or populations.
Notations:
- \(Y_{ij}\) = Observation from subject j in group i
- \(n_{i}\) = Number of subjects in group i
- \(N = n_{1} + n_{2} + \dots + n_{g}\) = Total sample size.
Assumptions for the Analysis of Variance are the same as for a two-sample t-test except that there are more than two groups:
- The data from group i has common mean = \(\mu_{i}\); i.e., \(E\left(Y_{ij}\right) = \mu_{i}\) . This means that there are no sub-populations with different means.
- Homoskedasticity: The data from all groups have common variance \(\sigma^2\); i.e., \(var(Y_{ij}) = \sigma^{2}\). That is, the variability in the data does not depend on group membership.
- Independence: The subjects are independently sampled.
- Normality: The data are normally distributed.
The hypothesis of interest is that all of the means are equal. Mathematically we write this as:
\(H_0\colon \mu_1 = \mu_2 = \dots = \mu_g\)
The alternative is expressed as:
\(H_a\colon \mu_i \ne \mu_j \) for at least one \(i \ne j\).
i.e., there is a difference between at least one pair of group population means. The following notation should be considered:
This involves taking an average of all the observations for j = 1 to \(n_{i}\) belonging to the ith group. The dot in the second subscript means that the average involves summing over the second subscript of y.
This involves taking the average of all the observations within each group and over the groups and dividing by the total sample size. The double dots indicate that we are summing over both subscripts of y.
- \(\bar{y}_{i.} = \frac{1}{n_i}\sum_{j=1}^{n_i}Y_{ij}\) = Sample mean for group i .
- \(\bar{y}_{..} = \frac{1}{N}\sum_{i=1}^{g}\sum_{j=1}^{n_i}Y_{ij}\) = Grand mean.
- ANOVA
- The Analysis of Variance involves the partitioning of the total sum of squares which is defined as in the expression below:
- \(SS_{total} = \sum\limits_{i=1}^{g}\sum\limits_{j=1}^{n_i}(Y_{ij}-\bar{y}_{..})^2\)
Here we are looking at the average squared difference between each observation and the grand mean. Note that if the observations tend to be far away from the Grand Mean then this will take a large value. Conversely, if all of the observations tend to be close to the Grand mean, this will take a small value. Thus, the total sum of squares measures the variation of the data about the Grand mean.
An Analysis of Variance (ANOVA) is a partitioning of the total sum of squares. In the second line of the expression below, we are adding and subtracting the sample mean for the ith group. In the third line, we can divide this out into two terms, the first term involves the differences between the observations and the group means, \(\bar{y}_i\), while the second term involves the differences between the group means and the grand mean.
\(\begin{array}{lll} SS_{total} & = & \sum_{i=1}^{g}\sum_{j=1}^{n_i}\left(Y_{ij}-\bar{y}_{..}\right)^2 \\ & = & \sum_{i=1}^{g}\sum_{j=1}^{n_i}\left((Y_{ij}-\bar{y}_{i.})+(\bar{y}_{i.}-\bar{y}_{..})\right)^2 \\ & = &\underset{SS_{error}}{\underbrace{\sum_{i=1}^{g}\sum_{j=1}^{n_i}(Y_{ij}-\bar{y}_{i.})^2}}+\underset{SS_{treat}}{\underbrace{\sum_{i=1}^{g}n_i(\bar{y}_{i.}-\bar{y}_{..})^2}} \end{array}\)
The first term is called the error sum of squares and measures the variation in the data about their group means.
Note that if the observations tend to be close to their group means, then this value will tend to be small. On the other hand, if the observations tend to be far away from their group means, then the value will be larger. The second term is called the treatment sum of squares and involves the differences between the group means and the Grand mean. Here, if group means are close to the Grand mean, then this value will be small. While, if the group means tend to be far away from the Grand mean, this will take a large value. This second term is called the Treatment Sum of Squares and measures the variation of the group means about the Grand mean.
The Analysis of Variance results is summarized in an analysis of variance table below:
Hover over the light bulb to get more information on that item.
|
Source |
d.f. |
SS |
MS |
F |
|---|---|---|---|---|
|
Treatments |
\(g-1\) |
\(\sum _ { i = 1 } ^ { g } n _ { i } \left( \overline { y } _ { i . } - \overline { y } _ { . . } \right) ^ { 2 }\) |
\(\dfrac { S S _ { \text { treat } } } { g - 1 }\) |
\(\dfrac { M S _ { \text { treat } } } { M S _ { \text { error } } }\) |
|
Error |
\(N-g\) |
\(\sum _ { i = 1 } ^ { g } \sum _ { j = 1 } ^ { n _ { i } } \left( Y _ { i j } - \overline { y } _ { i . } \right) ^ { 2 }\) |
\(\dfrac { S S _ { \text { error } } } { N - g }\) |
|
|
Total |
\(N-1\) |
\(\sum _ { i = 1 } ^ { g } \sum _ { j = 1 } ^ { n _ { i } } \left( Y _ { i j } - \overline { y } _ { \dots } \right) ^ { 2 }\) |
The ANOVA table contains columns for Source, Degrees of Freedom, Sum of Squares, Mean Square and F. Sources include Treatment and Error which together add up to the Total.
The degrees of freedom for treatment in the first row of the table are calculated by taking the number of groups or treatments minus 1. The total degree of freedom is the total sample size minus 1. The Error degrees of freedom are obtained by subtracting the treatment degrees of freedom from the total degrees of freedom to obtain N-g.
The formulae for the Sum of Squares are given in the SS column. The Mean Square terms are obtained by taking the Sums of Squares terms and dividing them by the corresponding degrees of freedom.
The final column contains the F statistic which is obtained by taking the MS for treatment and dividing it by the MS for Error.
Under the null hypothesis that the treatment effect is equal across group means, that is \(H_{0} \colon \mu_{1} = \mu_{2} = \dots = \mu_{g} \), this F statistic is F-distributed with g - 1 and N - g degrees of freedom:
\(F \sim F_{g-1, N-g}\)
The numerator degrees of freedom g - 1 comes from the degrees of freedom for treatments in the ANOVA table. This is referred to as the numerator degrees of freedom since the formula for the F-statistic involves the Mean Square for Treatment in the numerator. The denominator degrees of freedom N - g is equal to the degrees of freedom for error in the ANOVA table. This is referred to as the denominator degrees of freedom because the formula for the F-statistic involves the Mean Square Error in the denominator.
We reject \(H_{0}\) at level \(\alpha\) if the F statistic is greater than the critical value of the F-table, with g - 1 and N - g degrees of freedom, and evaluated at level \(\alpha\).
\(F > F_{g-1, N-g, \alpha}\)
8.2 - The Multivariate Approach: One-way Multivariate Analysis of Variance (One-way MANOVA)
8.2 - The Multivariate Approach: One-way Multivariate Analysis of Variance (One-way MANOVA)Now we will consider the multivariate analog, the Multivariate Analysis of Variance, often abbreviated as MANOVA.
Suppose that we have data on p variables which we can arrange in a table such as the one below:
| Treatment | |||||
|---|---|---|---|---|---|
| 1 | 2 | \(\cdots\) | g | ||
| Subject | |||||
| Treatment 1 | \(\mathbf{Y_{11}} = \begin{pmatrix} Y_{111} \\ Y_{112} \\ \vdots \\ Y_{11p} \end{pmatrix}\) | \(\mathbf{Y_{21}} = \begin{pmatrix} Y_{211} \\ Y_{212} \\ \vdots \\ Y_{21p} \end{pmatrix}\) | \(\cdots\) | \(\mathbf{Y_{g1}} = \begin{pmatrix} Y_{g11} \\ Y_{g12} \\ \vdots \\ Y_{g1p} \end{pmatrix}\) | |
| Treatment 2 | \(\mathbf{Y_{12}} = \begin{pmatrix} Y_{121} \\ Y_{122} \\ \vdots \\ Y_{12p} \end{pmatrix}\) | \(\mathbf{Y_{22}} = \begin{pmatrix} Y_{221} \\ Y_{222} \\ \vdots \\ Y_{22p} \end{pmatrix}\) | \(\cdots\) | \(\mathbf{Y_{g2}} = \begin{pmatrix} Y_{g21} \\ Y_{g22} \\ \vdots \\ Y_{g2p} \end{pmatrix}\) | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | ||
| \(n_i\) | \(\mathbf{Y_{1n_1}} = \begin{pmatrix} Y_{1n_{1}1} \\ Y_{1n_{1}2} \\ \vdots \\ Y_{1n_{1}p} \end{pmatrix}\) | \(\mathbf{Y_{2n_2}} = \begin{pmatrix} Y_{2n_{2}1} \\ Y_{2n_{2}2} \\ \vdots \\ Y_{2n_{2}p} \end{pmatrix}\) | \(\cdots\) | \(\mathbf{Y_{gn_{g}}} = \begin{pmatrix} Y_{gn_{g^1}} \\ Y_{gn_{g^2}} \\ \vdots \\ Y_{gn_{2}p} \end{pmatrix}\) | |
In this multivariate case the scalar quantities, \(Y_{ij}\), of the corresponding table in ANOVA, are replaced by vectors having p observations.
Notation
\(n_{i}\) = the number of subjects in group i
\(N = n _ { 1 } + n _ { 2 } + \ldots + n _ { g }\) = Total sample size.
Assumptions
The assumptions here are essentially the same as the assumptions in Hotelling's \(T^{2}\) test, only here they apply to groups:
- The data from group i has common mean vector \(\boldsymbol{\mu}_i = \left(\begin{array}{c}\mu_{i1}\\\mu_{i2}\\\vdots\\\mu_{ip}\end{array}\right)\)
- The data from all groups have a common variance-covariance matrix \(\Sigma\).
- Independence: The subjects are independently sampled.
- Normality: The data are multivariate normally distributed.
Here we are interested in testing the null hypothesis that the group mean vectors are all equal to one another. Mathematically this is expressed as:
\(H_0\colon \boldsymbol{\mu}_1 = \boldsymbol{\mu}_2 = \dots = \boldsymbol{\mu}_g\)
The alternative hypothesis is:
\(H_a \colon \mu_{ik} \ne \mu_{jk}\) for at least one \(i \ne j\) and at least one variable \(k\)
This says that the null hypothesis is false if at least one pair of treatments is different on at least one variable.
Notation
The scalar quantities used in the univariate setting are replaced by vectors in the multivariate setting:
Sample Mean Vector
\(\bar{\mathbf{y}}_{i.} = \frac{1}{n_i}\sum_{j=1}^{n_i}\mathbf{Y}_{ij} = \left(\begin{array}{c}\bar{y}_{i.1}\\ \bar{y}_{i.2} \\ \vdots \\ \bar{y}_{i.p}\end{array}\right)\) = sample mean vector for group i . This sample mean vector is comprised of the group means for each of the p variables. Thus, \(\bar{y}_{i.k} = \frac{1}{n_i}\sum_{j=1}^{n_i}Y_{ijk}\) = sample mean vector for variable k in group i .
Grand Mean Vector
\(\bar{\mathbf{y}}_{..} = \frac{1}{N}\sum_{i=1}^{g}\sum_{j=1}^{n_i}\mathbf{Y}_{ij} = \left(\begin{array}{c}\bar{y}_{..1}\\ \bar{y}_{..2} \\ \vdots \\ \bar{y}_{..p}\end{array}\right)\) = grand mean vector. This grand mean vector is comprised of the grand means for each of the p variables. Thus, \(\bar{y}_{..k} = \frac{1}{N}\sum_{i=1}^{g}\sum_{j=1}^{n_i}Y_{ijk}\) = grand mean for variable k.
Total Sum of Squares and Cross Products
In the univariate Analysis of Variance, we defined the Total Sums of Squares, a scalar quantity. The multivariate analog is the Total Sum of Squares and Cross Products matrix, a p x p matrix of numbers. The total sum of squares is a cross products matrix defined by the expression below:
\(\mathbf{T = \sum\limits_{i=1}^{g}\sum_\limits{j=1}^{n_i}(Y_{ij}-\bar{y}_{..})(Y_{ij}-\bar{y}_{..})'}\)
Here we are looking at the differences between the vectors of observations \(Y_{ij}\) and the Grand mean vector. These differences form a vector which is then multiplied by its transpose.
Here, the \(\left (k, l \right )^{th}\) element of T is
\(\sum\limits_{i=1}^{g}\sum\limits_{j=1}^{n_i} (Y_{ijk}-\bar{y}_{..k})(Y_{ijl}-\bar{y}_{..l})\)
For k = l, this is the total sum of squares for variable k and measures the total variation in the \(k^{th}\) variable. For \(k ≠ l\), this measures the dependence between variables k and l across all of the observations.
We may partition the total sum of squares and cross products as follows:
\(\begin{array}{lll}\mathbf{T} & = & \mathbf{\sum_{i=1}^{g}\sum_{j=1}^{n_i}(Y_{ij}-\bar{y}_{..})(Y_{ij}-\bar{y}_{..})'} \\ & = & \mathbf{\sum_{i=1}^{g}\sum_{j=1}^{n_i}\{(Y_{ij}-\bar{y}_i)+(\bar{y}_i-\bar{y}_{..})\}\{(Y_{ij}-\bar{y}_i)+(\bar{y}_i-\bar{y}_{..})\}'} \\ & = & \mathbf{\underset{E}{\underbrace{\sum_{i=1}^{g}\sum_{j=1}^{n_i}(Y_{ij}-\bar{y}_{i.})(Y_{ij}-\bar{y}_{i.})'}}+\underset{H}{\underbrace{\sum_{i=1}^{g}n_i(\bar{y}_{i.}-\bar{y}_{..})(\bar{y}_{i.}-\bar{y}_{..})'}}}\end{array}\)
where E is the Error Sum of Squares and Cross Products, and H is the Hypothesis Sum of Squares and Cross Products.
The \(\left (k, l \right )^{th}\) element of the error sum of squares and cross products matrix E is:
\(\sum_\limits{i=1}^{g}\sum\limits_{j=1}^{n_i}(Y_{ijk}-\bar{y}_{i.k})(Y_{ijl}-\bar{y}_{i.l})\)
For k = l, this is the error sum of squares for variable k, and measures the within treatment variation for the \(k^{th}\) variable. For \(k ≠ l\), this measures the dependence between variables k and l after taking into account the treatment.
The \(\left (k, l \right )^{th}\) element of the hypothesis sum of squares and cross products matrix H is
\(\sum\limits_{i=1}^{g}n_i(\bar{y}_{i.k}-\bar{y}_{..k})(\bar{y}_{i.l}-\bar{y}_{..l})\)
For k = l, this is the treatment sum of squares for variable k and measures the between-treatment variation for the \(k^{th}\) variable. For \(k ≠ l\), this measures the dependence of variables k and l across treatments.
The partitioning of the total sum of squares and cross-products matrix may be summarized in the multivariate analysis of the variance table:
| Source | d.f. | SSP |
|---|---|---|
| Treatments | g - 1 | H |
| Error | N - g | E |
| Total | N - 1 | T |
We wish to reject
\(H_0\colon \boldsymbol{\mu_1 = \mu_2 = \dots =\mu_g}\)
if the hypothesis sum of squares and cross products matrix H is large relative to the error sum of squares and cross products matrix E.
8.3 - Test Statistics for MANOVA
8.3 - Test Statistics for MANOVASAS uses four different test statistics based on the MANOVA table:
- Wilks Lambda
\(\Lambda^* = \dfrac{|\mathbf{E}|}{|\mathbf{H+E}|}\)
Here, the determinant of the error sums of squares and cross-products matrix E is divided by the determinant of the total sum of squares and cross-products matrix T = H + E. If H is large relative to E, then |H + E| will be large relative to |E|. Thus, we will reject the null hypothesis if Wilks lambda is small (close to zero).
- Hotelling-Lawley Trace
\(T^2_0 = trace(\mathbf{HE}^{-1})\)
Here, we are multiplying H by the inverse of E; then we take the trace of the resulting matrix. If H is large relative to E, then the Hotelling-Lawley trace will take a large value. Thus, we will reject the null hypothesis if this test statistic is large.
- Pillai Trace
\(V = trace(\mathbf{H(H+E)^{-1}})\)
Here, we are multiplying H by the inverse of the total sum of squares and cross products matrix T = H + E. If H is large relative to E, then the Pillai trace will take a large value. Thus, we will reject the null hypothesis if this test statistic is large.
- Roy's Maximum Root: Largest eigenvalue of HE-1
Here, we multiply H by the inverse of E and then compute the largest eigenvalue of the resulting matrix. If H is large relative to E, then Roy's root will take a large value. Thus, we will reject the null hypothesis if this test statistic is large.
Recall: The trace of a p x p matrix
\(\mathbf{A} = \left(\begin{array}{cccc}a_{11} & a_{12} & \dots & a_{1p}\\ a_{21} & a_{22} & \dots & a_{2p} \\ \vdots & \vdots & & \vdots \\ a_{p1} & a_{p2} & \dots & a_{pp}\end{array}\right)\)
is equal to
\(trace(\mathbf{A}) = \sum_{i=1}^{p}a_{ii}\)
Statistical tables are not available for the above test statistics. However, each of the above test statistics has an F approximation: The following details the F approximations for Wilks lambda. Details for all four F approximations can be found on the SAS website.
1. Wilks Lambda
\begin{align} \text{Starting with }&& \Lambda^* &= \dfrac{|\mathbf{E}|}{|\mathbf{H+E}|}\\ \text{Let, }&& a &= N-g - \dfrac{p-g+2}{2},\\ &&\text{} b &= \left\{\begin{array}{ll} \sqrt{\frac{p^2(g-1)^2-4}{p^2+(g-1)^2-5}}; &\text{if } p^2 + (g-1)^2-5 > 0\\ 1; & \text{if } p^2 + (g-1)^2-5 \le 0 \end{array}\right. \\ \text{and}&& c &= \dfrac{p(g-1)-2}{2} \\ \text{Then}&& F &= \left(\dfrac{1-\Lambda^{1/b}}{\Lambda^{1/b}}\right)\left(\dfrac{ab-c}{p(g-1)}\right) \overset{\cdot}{\sim} F_{p(g-1), ab-c} \\ \text{Under}&& H_{o} \end{align}
8.4 - Example: Pottery Data - Checking Model Assumptions
8.4 - Example: Pottery Data - Checking Model AssumptionsExample 8-1 Pottery Data (MANOVA)
Before carrying out a MANOVA, first, check the model assumptions:
- The data from group i has common mean vector \(\boldsymbol{\mu}_{i}\)
- The data from all groups have a common variance-covariance matrix \(\Sigma\).
- Independence: The subjects are independently sampled.
- Normality: The data are multivariate normally distributed.
Assumptions
-
Assumption 1: The data from group i have a common mean vector \(\boldsymbol{\mu}_{i}\)
This assumption says that there are no subpopulations with different mean vectors. Here, this assumption might be violated if pottery collected from the same site had inconsistencies.
-
Assumption 3: Independence: The subjects are independently sampled. This assumption is satisfied if the assayed pottery is obtained by randomly sampling the pottery collected from each site. This assumption would be violated if, for example, pottery samples were collected in clusters. In other applications, this assumption may be violated if the data were collected over time or space.
-
Assumption 4: Normality: The data are multivariate normally distributed.
- For large samples, the Central Limit Theorem says that the sample mean vectors are approximately multivariate normally distributed, even if the individual observations are not.
- For the pottery data, however, we have a total of only N = 26 observations, including only two samples from Caldicot. With a small N, we cannot rely on the Central Limit Theorem.
Diagnostic procedures are based on the residuals, computed by taking the differences between the individual observations and the group means for each variable:
\(\hat{\epsilon}_{ijk} = Y_{ijk}-\bar{Y}_{i.k}\)
Thus, for each subject (or pottery sample in this case), residuals are defined for each of the p variables. Then, to assess normality, we apply the following graphical procedures:
- Plot the histograms of the residuals for each variable. Look for a symmetric distribution.
- Plot a matrix of scatter plots. Look for elliptical distributions and outliers.
- Plot three-dimensional scatter plots. Look for elliptical distributions and outliers.
If the histograms are not symmetric or the scatter plots are not elliptical, this would be evidence that the data are not sampled from a multivariate normal distribution in violation of Assumption 4. In this case, a normalizing transformation should be considered.
Download the text file containing the data here: pottery.csv
The SAS program below will help us check this assumption.
Download the SAS Program here: potterya.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Check for normality - Pottery Data";
data pottery;
infile "D:\Statistics\STAT 505\data\pottery.csv" delimiter=',' firstobs=2;
input site $ al fe mg ca na;
run;
/* The class statement specifies the categorical variable site.
* The model statement specifies the five responses to the left
* and the categorical predictor to the right of the = sign.
* The output statement is optional and can be used to save the
* residuals, which are named with the r= option for later use.
*/
proc glm data=pottery;
class site;
model al fe mg ca na = site;
output out=resids r=ral rfe rmg rca rna;
run;
proc print data=resids;
run;
MANOVA normality assumption
To fit the MANOVA model and assess the normality of residuals in Minitab:
- Open the ‘pottery’ data set in a new worksheet
- For convenience, rename the columns: site, al, fe, mg, ca, and na from left to right.
- Stat > ANOVA > General MANOVA
- Highlight and select all five variables (al through na) to move them to the Responses window
- Highlight and select 'site' to move it to the Model window.
- Graphs > Individual plots, check Histogram and Normal plot, then 'OK'.
- Choose 'OK' again. The MANOVA table, along with the residual plots are displayed in the results area.
- Histograms suggest that, except for sodium, the distributions are relatively symmetric. However, the histogram for sodium suggests that there are two outliers in the data. Both of these outliers are in Llanadyrn.
- Two outliers can also be identified from the matrix of scatter plots.
- Removal of the two outliers results in a more symmetric distribution for sodium.
The results of MANOVA can be sensitive to the presence of outliers. One approach to assessing this would be to analyze the data twice, once with the outliers and once without them. The results may then be compared for consistency. The following analyses use all of the data, including the two outliers.
Assumption 2: The data from all groups have a common variance-covariance matrix \(\Sigma\).
This assumption can be checked using Box's test for homogeneity of variance-covariance matrices. To obtain Box's test, let \(\Sigma_{i}\) denote the population variance-covariance matrix for group i . Consider testing:
\(H_0\colon \Sigma_1 = \Sigma_2 = \dots = \Sigma_g\)
against
\(H_0\colon \Sigma_i \ne \Sigma_j\) for at least one \(i \ne j\)
Under the alternative hypothesis, at least two of the variance-covariance matrices differ on at least one of their elements. Let:
\(\mathbf{S}_i = \dfrac{1}{n_i-1}\sum\limits_{j=1}^{n_i}\mathbf{(Y_{ij}-\bar{y}_{i.})(Y_{ij}-\bar{y}_{i.})'}\)
denote the sample variance-covariance matrix for group i . Compute the pooled variance-covariance matrix
\(\mathbf{S}_p = \dfrac{\sum_{i=1}^{g}(n_i-1)\mathbf{S}_i}{\sum_{i=1}^{g}(n_i-1)}= \dfrac{\mathbf{E}}{N-g}\)
Box's test is based on the following test statistic:
\(L' = c\left\{(N-g)\log |\mathbf{S}_p| - \sum_{i=1}^{g}(n_i-1)\log|\mathbf{S}_i|\right\}\)
where the correction factor is
\(c = 1-\dfrac{2p^2+3p-1}{6(p+1)(g-1)}\left\{\sum_\limits{i=1}^{g}\dfrac{1}{n_i-1}-\dfrac{1}{N-g}\right\}\)
The version of Box's test considered in the lesson of the two-sample Hotelling's T-square is a special case where g = 2. Under the null hypothesis of homogeneous variance-covariance matrices, L' is approximately chi-square distributed with
\(\dfrac{1}{2}p(p+1)(g-1)\)
degrees of freedom. Reject \(H_0\) at level \(\alpha\) if
\(L' > \chi^2_{\frac{1}{2}p(p+1)(g-1),\alpha}\)
Example 8-2: Pottery Data
Here we will use the Pottery SAS program.
Download the SAS Program here: pottery2.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Box's Test - Pottery Data";
data pottery;
infile "D:\Statistics\STAT 505\data\pottery.csv" delimiter=',' firstobs=2;
input site $ al fe mg ca na;
run;
/* The pool option specifies that covariance matrices should be pooled.
* The class statement specifies the categorical variable site.
* The var statement specifies the five variables to be used to
* calculate the covariance matrix.
*/
proc discrim data=pottery pool=test;
class site;
var al fe mg ca na;
run;
Minitab does not perform this function at this time.
Analysis
We find no statistically significant evidence against the null hypothesis that the variance-covariance matrices are homogeneous (L' = 27.58; d.f. = 45; p = 0.98).
Notes
- If we were to reject the null hypothesis of homogeneity of variance-covariance matrices, then we would conclude that assumption 2 is violated.
- MANOVA is not robust to violations of the assumption of homogeneous variance-covariance matrices.
- If the variance-covariance matrices are determined to be unequal then the solution is to find a variance-stabilizing transformation.
- Note that the assumptions of homogeneous variance-covariance matrices and multivariate normality are often violated together.
- Therefore, a normalizing transformation may also be a variance-stabilizing transformation.
8.5 - Example: MANOVA of Pottery Data
8.5 - Example: MANOVA of Pottery DataExample 8-3: Pottery Data (MANOVA)
After we have assessed the assumptions, our next step is to proceed with the MANOVA.
This may be carried out using the Pottery SAS Program below.
Download the SAS Program here: pottery.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "MANOVA - Pottery Data";
data pottery;
infile "D:\Statistics\STAT 505\data\pottery.csv" delimiter=',' firstobs=2;
input site $ al fe mg ca na;
run;
proc print data=pottery;
run;
/* The class statement specifies the categorical variable site.
* The model statement specifies the five responses to the left
* and the categorical predictor to the right of the = sign.
*/
proc glm data=pottery;
class site;
model al fe mg ca na = site;
/* The contrast statements are used to calculate test statistics
* and p-values for combinations of the groups.
* The initial strings in quotes are arbitrary names,
* followed by the name of the categorical variable defining the
* groups, and the coefficients multiplying each group mean.
*/
contrast 'C+L-A-I' site 8 -2 8 -14;
contrast 'A vs I ' site 1 0 -1 0;
contrast 'C vs L ' site 0 1 0 -1;
/* The estimate statements are used to calculate estimates and
* standard errors for combinations of the groups.
* The divisor option divides the contrast by the value specified.
*/
estimate 'C+L-A-I' site 8 -2 8 -14/ divisor=16;
estimate 'A vs I ' site 1 0 -1 0;
estimate 'C vs L ' site 0 1 0 -1;
/* The lsmeans option provides standard error estimates and
* standard errors for the differences between the site groups.
* The manova statement is used for multivariate tests and results.
* The h= option specifies the groups for comparison, and the
* options printe and printh display the sums of squares and cross
* products matrices for error and the hypothesis, respectively.
*/
lsmeans site / stderr;
manova h=site / printe printh;
run;
Performing a MANOVA
To carry out the MANOVA test in Minitab:
- Open the ‘pottery’ data set in a new worksheet
- For convenience, rename the columns: site, al, fe, mg, ca, and na from left to right.
- Stat > ANOVA > General MANOVA
- Highlight and select all five variables (al through na) to move them to the Responses window
- Highlight and select 'site' to move it to the Model window. Choose 'OK'.
- Choose 'OK' again. The MANOVA table is displayed in the results area.
Analysis
The concentrations of the chemical elements depend on the site where the pottery sample was obtained \(\left( \Lambda ^ { \star } = 0.0123; F = 13.09; \mathrm { d } . \mathrm { f } = 15,50 ; p < 0.0001 \right)\). It was found, therefore, that there are differences in the concentrations of at least one element between at least one pair of sites.
Question: How do the chemical constituents differ among sites?
A profile plot may be used to explore how the chemical constituents differ among the four sites. In a profile plot, the group means are plotted on the Y-axis against the variable names on the X-axis, connecting the dots for all means within each group. A profile plot for the pottery data is obtained using the SAS program below
Download the SAS Program here: pottery1.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Profile Plot for Pottery Data";
/* After reading in the pottery data, where each variable is
* originally in its own column, the next statements stack the data
* so that all variable names are in one column called 'chemical',
* and all response values are in another column called 'amount'.
* This format is used for the calculations that follow, as well
* as for the profile plot.
*/
data pottery;
infile "D:\Statistics\STAT 505\data\pottery.csv" delimiter=',' firstobs=2;
input site $ al fe mg ca na;
chemical="al"; amount=al; output;
chemical="fe"; amount=fe; output;
chemical="mg"; amount=mg; output;
chemical="ca"; amount=ca; output;
chemical="na"; amount=na; output;
proc sort data=pottery;
by site chemical;
run;
/* The means procedure calculates and saves the mean amount,
* for each site and chemical. It then saves these results
* in a new data set 'a' for use in the steps below.
* /
proc means data=pottery;
by site chemical;
var amount;
output out=a mean=mean;
run;
/* The axis commands define the size of the plotting window.
* The horizontal axis is of the chemicals, and the vertical
* axis is used for the means. Using the =site syntax also
* separates these plotted means by site.
* /
proc gplot data=a;
axis1 length=3 in;
axis2 length=4.5 in;
plot mean*chemical=site / vaxis=axis1 haxis=axis2;
symbol1 v=J f=special h=2 l=1 i=join color=black;
symbol2 v=K f=special h=2 l=1 i=join color=black;
symbol3 v=L f=special h=2 l=1 i=join color=black;
symbol4 v=M f=special h=2 l=1 i=join color=black;
run;
MANOVA profile plot
To create a profile plot in Minitab:
- Open the ‘pottery’ data set in a new worksheet
- For convenience, rename the columns: site, al, fe, mg, ca, and na from left to right.
- Graph > Line plots > Multiple Y’s
- Highlight and select all five variables (al through na) to move them to Graph variables.
- Highlight and select 'site' to move it to the Categorical variable for grouping.
- Choose 'OK'. The profile plot is displayed in the results area. Note that the order of the variables on the plot corresponds to the original order in the data set.
Analysis
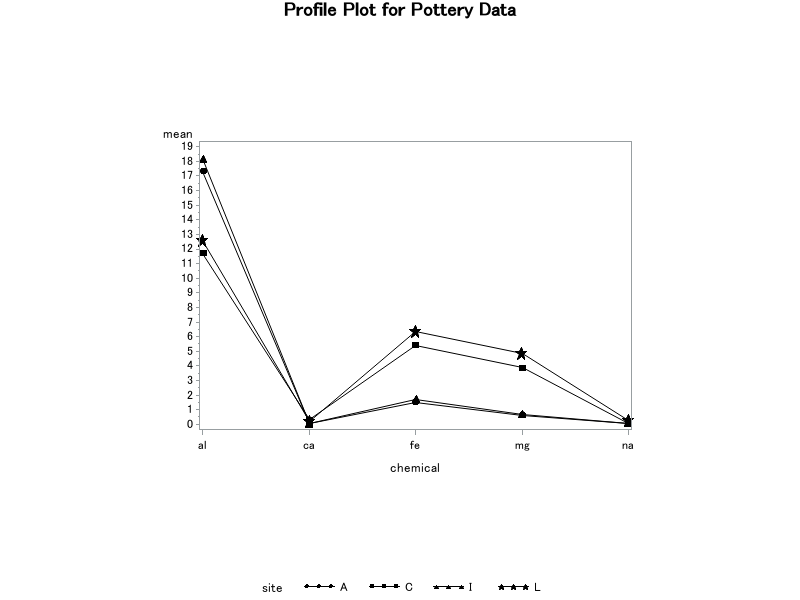
Results from the profile plots are summarized as follows:
- The sample sites appear to be paired: Ashley Rails with Isle Thorns and Caldicot with Llanedyrn.
- Ashley Rails and Isle Thorns appear to have higher aluminum concentrations than Caldicot and Llanedyrn.
- Caldicot and Llanedyrn appear to have higher iron and magnesium concentrations than Ashley Rails and Isle Thorns.
- Calcium and sodium concentrations do not appear to vary much among the sites.
Note: These results are not backed up by appropriate hypotheses tests. Hypotheses need to be formed to answer specific questions about the data. These should be considered only if significant differences among group mean vectors are detected in the MANOVA.
Specific Questions
- Which chemical elements vary significantly across sites?
- How do the sites differ?
- Is the mean chemical constituency of pottery from Ashley Rails and Isle Thorns different from that of Llanedyrn and Caldicot?
- Is the mean chemical constituency of pottery from Ashley Rails equal to that of Isle Thorns?
- Is the mean chemical constituency of pottery from Llanedyrn equal to that of Caldicot?
Analysis of Individual Chemical Elements
A naive approach to assessing the significance of individual variables (chemical elements) would be to carry out individual ANOVAs to test:
\(H_0\colon \mu_{1k} = \mu_{2k} = \dots = \mu_{gk}\)
for chemical k. Reject \(H_0 \) at level \(\alpha\) if
\(F > F_{g-1, N-g, \alpha}\)
Problem: If we're going to repeat this analysis for each of the p variables, this does not control for the experiment-wise error rate.
Just as we can apply a Bonferroni correction to obtain confidence intervals, we can also apply a Bonferroni correction to assess the effects of group membership on the population means of the individual variables.
Bonferroni Correction: Reject \(H_0 \) at level \(\alpha\) if
\(F > F_{g-1, N-g, \alpha/p}\)
or, equivalently, if the p-value is less than \(α/p\).
Example 8-4: Pottery Data (ANOVA)
The results for individual ANOVA results are output with the SAS program below.
Download the SAS program here: pottery.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "MANOVA - Pottery Data";
data pottery;
infile "D:\Statistics\STAT 505\data\pottery.csv" delimiter=',' firstobs=2;
input site $ al fe mg ca na;
run;
proc print data=pottery;
run;
/* The class statement specifies the categorical variable site.
* The model statement specifies the five responses to the left
* and the categorical predictor to the right of the = sign.
*/
proc glm data=pottery;
class site;
model al fe mg ca na = site;
/* The contrast statements are used to calculate test statistics
* and p-values for combinations of the groups.
* The initial strings in quotes are arbitrary names,
* followed by the name of the categorical variable defining the
* groups, and the coefficients multiplying each group mean.
*/
contrast 'C+L-A-I' site 8 -2 8 -14;
contrast 'A vs I ' site 1 0 -1 0;
contrast 'C vs L ' site 0 1 0 -1;
/* The estimate statements are used to calculate estimates and
* standard errors for combinations of the groups.
* The divisor option divides the contrast by the value specified.
*/
estimate 'C+L-A-I' site 8 -2 8 -14/ divisor=16;
estimate 'A vs I ' site 1 0 -1 0;
estimate 'C vs L ' site 0 1 0 -1;
/* The lsmeans option provides standard error estimates and
* standard errors for the differences between the site groups.
* The manova statement is used for multivariate tests and results.
* The h= option specifies the groups for comparison, and the
* options printe and printh display the sums of squares and cross
* products matrices for error and the hypothesis, respectively.
*/
lsmeans site / stderr;
manova h=site / printe printh;
run;
MANOVA follow-up ANOVAs
To carry out multiple ANOVA tests in Minitab:
- Open the ‘pottery’ data set in a new worksheet
- For convenience, rename the columns: site, al, fe, mg, ca, and na from left to right.
- Stat > ANOVA > General Linear Model > Fit General Linear Model
- Highlight and select all five variables (al through na) to move them to the Responses window
- Highlight and select 'site' to move it to the Factors window.
- Choose 'OK'. Each of the ANOVA tables is displayed separately in the results area.
Analysis
Here, p = 5 variables, g = 4 groups, and a total of N = 26 observations. So, for an α = 0.05 level test, we reject
\(H_0\colon \mu_{1k} = \mu_{2k} = \dots = \mu_{gk}\)
if
\(F > F_{3,22,0.01} = 4.82\)
or equivalently, if the p-value reported by SAS is less than 0.05/5 = 0.01. The results of the individual ANOVAs are summarized in the following table. All tests are carried out with 3, 22 degrees freedom (the d.f. should always be noted when reporting these results).
| Element | F | SAS p-value |
|---|---|---|
| Al | 26.67 | < 0.0001 |
| Fe | 89.88 | < 0.0001 |
| Mg | 49.12 | < 0.0001 |
| Ca | 29.16 | < 0.0001 |
| Na | 9.50 | 0.0003 |
Because all of the F-statistics exceed the critical value of 4.82, or equivalently, because the SAS p-values all fall below 0.01, we can see that all tests are significant at the 0.05 level under the Bonferroni correction.
Conclusion: The means for all chemical elements differ significantly among the sites. For each element, the means for that element are different for at least one pair of sites.
8.6 - Orthogonal Contrasts
8.6 - Orthogonal ContrastsDifferences among treatments can be explored through pre-planned orthogonal contrasts. Contrasts involve linear combinations of group mean vectors instead of linear combinations of the variables.
- Contrasts
-
The linear combination of group mean vectors
\(\mathbf{\Psi} = \sum_\limits{i=1}^{g}c_i\mathbf{\mu}_i\)
is a (treatment) contrast if
\(\sum_\limits{i=1}^{g}c_i = 0\)
Contrasts are defined with respect to specific questions we might wish to ask of the data. Here, we shall consider testing hypotheses of the form
\(H_0\colon \mathbf{\Psi = 0}\)
Example 8-5: Drug Trial
Suppose that we have a drug trial with the following 3 treatments:
- Placebo
- Brand Name
- Generic
Consider the following questions:
Question 1: Is there a difference between the Brand Name drug and the Generic drug?
\begin{align} \text{That is, consider testing:}&& &H_0\colon \mathbf{\mu_2 = \mu_3}\\ \text{This is equivalent to testing,}&& &H_0\colon \mathbf{\Psi = 0}\\ \text{where,}&& &\mathbf{\Psi = \mu_2 - \mu_3} \\ \text{with}&& &c_1 = 0, c_2 = 1, c_3 = -1 \end{align}
Question 2: Are the drug treatments effective?
\begin{align} \text{That is, consider testing:}&& &H_0\colon \mathbf{\mu_1} = \frac{\mathbf{\mu_2+\mu_3}}{2}\\ \text{This is equivalent to testing,}&& &H_0\colon \mathbf{\Psi = 0}\\ \text{where,}&& &\mathbf{\Psi} = \mathbf{\mu}_1 - \frac{1}{2}\mathbf{\mu}_2 - \frac{1}{2}\mathbf{\mu}_3 \\ \text{with}&& &c_1 = 1, c_2 = c_3 = -\frac{1}{2}\end{align}
Estimation
The contrast
\(\mathbf{\Psi} = \sum_{i=1}^{g}c_i \mu_i\)
is estimated by replacing the population mean vectors with the corresponding sample mean vectors:
\(\mathbf{\hat{\Psi}} = \sum_{i=1}^{g}c_i\mathbf{\bar{Y}}_i.\)
Because the estimated contrast is a function of random data, the estimated contrast is also a random vector. So the estimated contrast has a population mean vector and population variance-covariance matrix. The population mean of the estimated contrast is \(\mathbf{\Psi}\). The variance-covariance matrix of \(\hat{\mathbf{\Psi}}\)¸ is:
\(\left(\sum\limits_{i=1}^{g}\frac{c^2_i}{n_i}\right)\Sigma\)
which is estimated by substituting the pooled variance-covariance matrix for the population variance-covariance matrix
\(\left(\sum\limits_{i=1}^{g}\frac{c^2_i}{n_i}\right)\mathbf{S}_p = \left(\sum\limits_{i=1}^{g}\frac{c^2_i}{n_i}\right) \dfrac{\mathbf{E}}{N-g}\)
- Orthogonal Contrasts
-
Two contrasts
\(\Psi_1 = \sum_{i=1}^{g}c_i\mathbf{\mu}_i\) and \(\Psi_2 = \sum_{i=1}^{g}d_i\mathbf{\mu}_i\)
are orthogonal if
\(\sum\limits_{i=1}^{g}\frac{c_id_i}{n_i}=0\)
The importance of orthogonal contrasts can be illustrated by considering the following paired comparisons:
\(H^{(1)}_0\colon \mu_1 = \mu_2\)
\(H^{(2)}_0\colon \mu_1 = \mu_3\)
\(H^{(3)}_0\colon \mu_2 = \mu_3\)
We might reject \(H^{(3)}_0\), but fail to reject \(H^{(1)}_0\) and \(H^{(2)}_0\). But, if \(H^{(3)}_0\) is false then both \(H^{(1)}_0\) and \(H^{(2)}_0\) cannot be true.
Notes
- For balanced data (i.e., \(n _ { 1 } = n _ { 2 } = \ldots = n _ { g }\) ), \(\mathbf{\Psi}_1\) and \(\mathbf{\Psi}_2\) are orthogonal contrasts if \(\sum_{i=1}^{g}c_id_i = 0\)
- If \(\mathbf{\Psi}_1\) and \(\mathbf{\Psi}_2\) are orthogonal contrasts, then the elements of \(\hat{\mathbf{\Psi}}_1\) and \(\hat{\mathbf{\Psi}}_2\) are uncorrelated
- If \(\mathbf{\Psi}_1\) and \(\mathbf{\Psi}_2\) are orthogonal contrasts, then the tests for \(H_{0} \colon \mathbf{\Psi}_1= 0\) and \(H_{0} \colon \mathbf{\Psi}_2= 0\) are independent of one another. That is, the results of the test have no impact on the results of the other test.
- For g groups, it is always possible to construct g - 1 mutually orthogonal contrasts.
- If \(\mathbf{\Psi}_1, \mathbf{\Psi}_2, \dots, \mathbf{\Psi}_{g-1}\) are orthogonal contrasts, then for each ANOVA table, the treatment sum of squares can be partitioned into \(SS_{treat} = SS_{\Psi_1}+SS_{\Psi_2}+\dots + SS_{\Psi_{g-1}} \)
- Similarly, the hypothesis sum of squares and cross-products matrix may be partitioned: \(\mathbf{H} = \mathbf{H}_{\Psi_1}+\mathbf{H}_{\Psi_2}+\dots\mathbf{H}_{\Psi_{g-1}}\)
8.7 - Constructing Orthogonal Contrasts
8.7 - Constructing Orthogonal ContrastsThe following shows two examples to construct orthogonal contrasts. In each example, we consider balanced data; that is, there are equal numbers of observations in each group.
Example 8-6:
In some cases, it is possible to draw a tree diagram illustrating the hypothesized relationships among the treatments. In the following tree, we wish to compare 5 different populations of subjects. Prior to collecting the data, we may have reason to believe that populations 2 and 3 are most closely related. Populations 4 and 5 are also closely related, but not as close as populations 2 and 3. Population 1 is closer to populations 2 and 3 than populations 4 and 5.
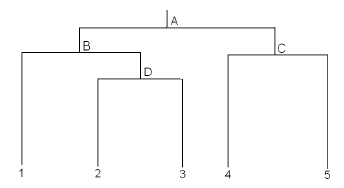
Each branch (denoted by the letters A, B, C, and D) corresponds to a hypothesis we may wish to test. This yields the contrast coefficients as shown in each row of the following table:
| Contrasts | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| A | \(\dfrac{1}{3}\) | \(\dfrac{1}{3}\) | \(\dfrac{1}{3}\) | \(- \dfrac { 1 } { 2 }\) | \(- \dfrac { 1 } { 2 }\) |
| B | 1 | \(- \dfrac { 1 } { 2 }\) | \(- \dfrac { 1 } { 2 }\) | 0 | 0 |
| C | 0 | 0 | 0 | 1 | -1 |
| D | 0 | 1 | -1 | 0 | 0 |
Consider Contrast A. Here, we are comparing the mean of all subjects in populations 1,2, and 3 to the mean of all subjects in populations 4 and 5.
For Contrast B, we compare population 1 (receiving a coefficient of +1) with the mean of populations 2 and 3 (each receiving a coefficient of -1/2). Multiplying the corresponding coefficients of contrasts A and B, we obtain:
(1/3) × 1 + (1/3) × (-1/2) + (1/3) × (-1/2) + (-1/2) × 0 + (-1/2) × 0 = 1/3 - 1/6 - 1/6 + 0 + 0 = 0
So contrasts A and B are orthogonal. Similar computations can be carried out to confirm that all remaining pairs of contrasts are orthogonal to one another.
Example 8-7:
Consider the factorial arrangement of drug type and drug dose treatments:
| Drug | Low | High |
|---|---|---|
| A | 1 | 2 |
| B | 3 | 4 |
Here, treatment 1 is equivalent to a low dose of drug A, treatment 2 is equivalent to a high dose of drug A, etc. For this factorial arrangement of drug type and drug dose treatments, we can form the orthogonal contrasts:
| Contrasts | A, Low | A, High | B, Low | B, High |
|---|---|---|---|---|
| Drug | \(- \dfrac{1}{2}\) | \(- \dfrac{1}{2}\) | \( \dfrac{1}{2}\) | \( \dfrac{1}{2}\) |
| Dose | \(- \dfrac{1}{2}\) | \( \dfrac{1}{2}\) | \(- \dfrac { 1 } { 2 }\) | \( \dfrac{1}{2}\) |
| Interaction | \( \dfrac{1}{2}\) | \(- \dfrac{1}{2}\) | \(- \dfrac{1}{2}\) | \( \dfrac{1}{2}\) |
To test for the effects of drug type, we give coefficients with a negative sign for drug A, and positive signs for drug B. Because there are two doses within each drug type, the coefficients take values of plus or minus 1/2.
Similarly, to test for the effects of drug dose, we give coefficients with negative signs for the low dose, and positive signs for the high dose. Because there are two drugs for each dose, the coefficients take values of plus or minus 1/2.
The final test considers the null hypothesis that the effect of the drug does not depend on the dose, or conversely, the effect of the dose does not depend on the drug. In either case, we are testing the null hypothesis that there is no interaction between the drug and dose. The coefficients for this interaction are obtained by multiplying the signs of the coefficients for drug and dose. Thus, for drug A at the low dose, we multiply "-" (for the drug effect) times "-" (for the dose-effect) to obtain "+" (for the interaction). Similarly, for drug A at the high dose, we multiply "-" (for the drug effect) times "+" (for the dose-effect) to obtain "-" (for the interaction). The remaining coefficients are obtained similarly.
Example 8-8: Pottery Data
Recall the specific questions:
- Does the mean chemical content of pottery from Ashley Rails and Isle Thorns equal that of pottery from Caldicot and Llanedyrn?
- Does the mean chemical content of pottery from Ashley Rails equal that of pottery from Isle Thorns?
- Does the mean chemical content of pottery from Caldicot equal that of pottery from Llanedyrn?
These questions correspond to the following theoretical relationships among the sites:
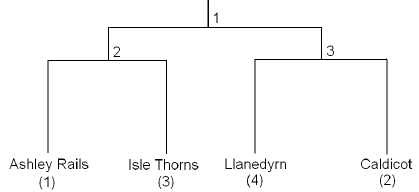
The relationships among sites suggested in the above figure suggest the following contrasts:
| Contrasts | Ashley Rails | Caldicot | Isle Thorns | Llanedyrn |
|---|---|---|---|---|
| 1 | \( \dfrac{1}{2}\) | \(- \dfrac{1}{2}\) | \( \dfrac{1}{2}\) | \(- \dfrac{1}{2}\) |
| 2 | 1 | 0 | -1 | 0 |
| 3 | 0 | 1 | 0 | -1 |
| \(n_i\) | 5 | 2 | 5 | 14 |
Notes
Contrasts 1 and 2 are orthogonal:
\[\sum_{i=1}^{g} \frac{c_id_i}{n_i} = \frac{0.5 \times 1}{5} + \frac{(-0.5)\times 0}{2}+\frac{0.5 \times (-1)}{5} +\frac{(-0.5)\times 0}{14} = 0\]
However, contrasts 1 and 3 are not orthogonal:
\[\sum_{i=1}^{g} \frac{c_id_i}{n_i} = \frac{0.5 \times 0}{5} + \frac{(-0.5)\times 1}{2}+\frac{0.5 \times 0}{5} +\frac{(-0.5)\times (-1) }{14} = \frac{6}{28}\]
Solution: Instead of estimating the mean of pottery collected from Caldicot and Llanedyrn by
\[\frac{\mathbf{\bar{y}_2+\bar{y}_4}}{2}\]
we can weigh by sample size:
\[\frac{n_2\mathbf{\bar{y}_2}+n_4\mathbf{\bar{y}_4}}{n_2+n_4} = \frac{2\mathbf{\bar{y}}_2+14\bar{\mathbf{y}}_4}{16}\]
Similarly, the mean of pottery collected from Ashley Rails and Isle Thorns may be estimated by
\[\frac{n_1\mathbf{\bar{y}_1}+n_3\mathbf{\bar{y}_3}}{n_1+n_3} = \frac{5\mathbf{\bar{y}}_1+5\bar{\mathbf{y}}_3}{10} = \frac{8\mathbf{\bar{y}}_1+8\bar{\mathbf{y}}_3}{16}\]
This yields the Orthogonal Contrast Coefficients:
| Contrasts | Ashley Rails | Caldicot | Isle Thorns | Llanedyrn |
|---|---|---|---|---|
| 1 | \( \dfrac{8}{16}\) | \(- \dfrac{2}{16}\) | \( \dfrac{8}{16}\) | \(- \dfrac{14}{16}\) |
| 2 | 1 | 0 | -1 | 0 |
| 3 | 0 | 1 | 0 | -1 |
| \(n_i\) | 5 | 2 | 5 | 14 |
The inspect button below will walk through how these contrasts are implemented in the SAS program.
Download the SAS program here: pottery.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "MANOVA - Pottery Data";
data pottery;
infile "D:\Statistics\STAT 505\data\pottery.csv" delimiter=',' firstobs=2;
input site $ al fe mg ca na;
run;
proc print data=pottery;
run;
/* The class statement specifies the categorical variable site.
* The model statement specifies the five responses to the left
* and the categorical predictor to the right of the = sign.
*/
proc glm data=pottery;
class site;
model al fe mg ca na = site;
/* The contrast statements are used to calculate test statistics
* and p-values for combinations of the groups.
* The initial strings in quotes are arbitrary names,
* followed by the name of the categorical variable defining the
* groups, and the coefficients multiplying each group mean.
*/
contrast 'C+L-A-I' site 8 -2 8 -14;
contrast 'A vs I ' site 1 0 -1 0;
contrast 'C vs L ' site 0 1 0 -1;
/* The estimate statements are used to calculate estimates and
* standard errors for combinations of the groups.
* The divisor option divides the contrast by the value specified.
*/
estimate 'C+L-A-I' site 8 -2 8 -14/ divisor=16;
estimate 'A vs I ' site 1 0 -1 0;
estimate 'C vs L ' site 0 1 0 -1;
/* The lsmeans option provides standard error estimates and
* standard errors for the differences between the site groups.
* The manova statement is used for multivariate tests and results.
* The h= option specifies the groups for comparison, and the
* options printe and printh display the sums of squares and cross
* products matrices for error and the hypothesis, respectively.
*/
lsmeans site / stderr;
manova h=site / printe printh;
run;
Orthogonal contrast for MANOVA is not available in Minitab at this time.
Analysis
The following table of estimated contrasts is obtained
| Element | \(\widehat { \Psi } _ { 1 }\) | \(\widehat { \Psi } _ { 2 }\) | \(\widehat { \Psi } _ { 3 }\) |
|---|---|---|---|
| Al | 5.29 | -0.86 | -0.86 |
| Fe | -4.64 | -0.20 | -0.96 |
| Mg | -4.06 | -0.07 | -0.97 |
| Ca | -0.17 | 0.03 | 0.09 |
| Na | -0.17 | -0.01 | -0.20 |
These results suggest:
- Pottery from Ashley Rails and Isle Thorns have higher aluminum and lower iron, magnesium, calcium, and sodium concentrations than pottery from Caldicot and Llanedyrn.
- Pottery from Ashley Rails has higher calcium and lower aluminum, iron, magnesium, and sodium concentrations than pottery from Isle Thorns.
- Pottery from Caldicot has higher calcium and lower aluminum, iron, magnesium, and sodium concentrations than pottery from Llanedyrn.
8.8 - Hypothesis Tests
8.8 - Hypothesis TestsProblem:
The suggestions dealt with in the previous page are not backed up by appropriate hypothesis tests. Consider hypothesis tests of the form:
\(H_0\colon \Psi = 0\) against \(H_a\colon \Psi \ne 0\)
Univariate Case:
For the univariate case, we may compute the sums of squares for the contrast:
\(SS_{\Psi} = \frac{\hat{\Psi}^2}{\sum_{i=1}^{g}\frac{c^2_i}{n_i}}\)
This sum of squares has only 1 d.f. so that the mean square for the contrast is
\(MS_{\Psi}= SS_{\Psi}\)
Then compute the F-ratio:
\(F = \frac{MS_{\Psi}}{MS_{error}}\)
Reject \(H_{0} \colon \Psi = 0\) at level \(\alpha\) if
\(F > F_{1, N-g, \alpha}\)
Multivariate Case
For the multivariate case, the sums of squares for the contrast is replaced by the hypothesis sum of squares and cross-products matrix for the contrast:
\(\mathbf{H}_{\mathbf{\Psi}} = \dfrac{\mathbf{\hat{\Psi}\hat{\Psi}'}}{\sum_{i=1}^{g}\frac{c^2_i}{n_i}}\)
Compute Wilks Lambda
\(\Lambda^* = \dfrac{|\mathbf{E}|}{\mathbf{|H_{\Psi}+E|}}\)
Compute the F-statistic
\(F = \left(\dfrac{1-\Lambda^*_{\mathbf{\Psi}}}{\Lambda^*_{\mathbf{\Psi}}}\right)\left(\dfrac{N-g-p+1}{p}\right)\)
Reject Ho : \(\mathbf{\Psi = 0} \) at level \(α\) if
\(F > F_{p, N-g-p+1, \alpha}\)
Example 8-9: Pottery Data
The following table gives the results of testing the null hypothesis that each of the contrasts is equal to zero. You should be able to find these numbers in the output by downloading the SAS program here: pottery.sas.
| Contrast | \(\Lambda _ { \Psi } ^ { * }\) | F | d.f | p |
|---|---|---|---|---|
| 1 | 0.0284 | 122.81 | 5, 18 | <0.0001 |
| 2 | 0.9126 | 0.34 | 5, 18 | 0.8788 |
| 3 | 0.4487 | 4.42 | 5, 18 | 0.0084 |
Conclusions
- The mean chemical content of pottery from Ashley Rails and Isle Thorns differs in at least one element from that of Caldicot and Llanedyrn \(\left( \Lambda _ { \Psi } ^ { * } = 0.0284; F = 122. 81; d.f. = 5, 18; p < 0.0001 \right) \).
- There is no significant difference in the mean chemical contents between Ashley Rails and Isle Thorns \(\left( \Lambda _ { \Psi } ^ { * } = 0.9126; F = 0.34; d.f. = 5, 18; p = 0.8788 \right) \).
- The mean chemical content of pottery from Caldicot differs in at least one element from that of Llanedyrn \(\left( \Lambda _ { \Psi } ^ { * } = 0.4487; F = 4.42; d.f. = 5, 18; p = 0.0084 \right) \).
Once we have rejected the null hypothesis that contrast is equal to zero, we can compute simultaneous or Bonferroni confidence intervals for the contrast:
Simultaneous Confidence Intervals
Simultaneous \((1 - α) × 100\%\) Confidence Intervals for the Elements of \(\Psi\) are obtained as follows:
\(\hat{\Psi}_j \pm \sqrt{\dfrac{p(N-g)}{N-g-p+1}F_{p, N-g-p+1}}SE(\hat{\Psi}_j)\)
where
\(SE(\hat{\Psi}_j) = \sqrt{\left(\sum\limits_{i=1}^{g}\dfrac{c^2_i}{n_i}\right)\dfrac{e_{jj}}{N-g}}\)
where \(e_{jj}\) is the \( \left( j, j \right)^{th}\) element of the error sum of squares and cross products matrix, and is equal to the error sums of squares for the analysis of variance of variable j.
Contrast 1
Recall that we have p = 5 chemical constituents, g = 4 sites, and a total of N = 26 observations. From the F-table, we have F5,18,0.05 = 2.77. Then our multiplier
\begin{align} M &= \sqrt{\frac{p(N-g)}{N-g-p+1}F_{5,18}}\\[10pt] &= \sqrt{\frac{5(26-4)}{26-4-5+1}\times 2.77}\\[10pt] &= 4.114 \end{align}
Simultaneous 95% Confidence Intervals are computed in the following table. The elements of the estimated contrast together with their standard errors are found at the bottom of each page, giving the results of the individual ANOVAs. For example, the estimated contrast from aluminum is 5.294 with a standard error of 0.5972. The fourth column is obtained by multiplying the standard errors by M = 4.114. So, for example, 0.5972 × 4.114 = 2.457. Finally, the confidence interval for aluminum is 5.294 plus/minus 2.457:
| Element | \(\widehat { \Psi }\) | SE\(\widehat { \Psi }\) | \(M \times SE \left(\widehat { \Psi }\right)\) | Confidence Interval |
|---|---|---|---|---|
| Al | 5.294 | 0.5972 | 2.457 | 2.837, 7.751 |
| Fe | -4.640 | 0.2844 | 1.170 | -5.810, -3.470 |
| Mg | -4.065 | 0.3376 | 1.389 | -5.454, -2.676 |
| Ca | -0.175 | 0.0195 | 0.080 | -0.255, -0.095 |
| Na | -0.175 | 0.0384 | 0.158 | -0.333, -0.017 |
Conclusion
Pottery from Ashley Rails and Isle Thorns have higher aluminum and lower iron, magnesium, calcium, and sodium concentrations than pottery from Caldicot and Llanedyrn.
Contrast 3
Simultaneous 95% Confidence Intervals for Contrast 3 are obtained similarly to those for Contrast 1.
| Element | \(\widehat{\Psi}\) | SE( \(\widehat{\Psi}\) ) | \(M\times SE(\widehat{\Psi})\) | Confidence Interval |
|---|---|---|---|---|
| Al | -0.864 | 1.1199 | 4.608 | -5.472, 3.744 |
| Fe | -0.957 | 0.5333 | 2.194 | -3.151, 1.237 |
| Mg | -0.971 | 0.6331 | 2.605 | -3.576, 1.634 |
| Ca | 0.093 | 0.0366 | 0.150 | -0.057, 0.243 |
| Na | -0.201 | 0.0719 | 0.296 | -0.497, 0.095 |
Conclusion
All of the above confidence intervals cover zero. Therefore, the significant difference between Caldicot and Llanedyrn appears to be due to the combined contributions of the various variables.
Bonferroni Confidence Intervals
Bonferroni \((1 - α) × 100\%\) Confidence Intervals for the Elements of Ψ are obtained as follows:
\(\hat{\Psi}_j \pm t_{N-g, \frac{\alpha}{2p}}SE(\hat{\Psi}_j)\)
where
\(SE(\hat{\Psi}_j) = \sqrt{\left(\sum\limits_{i=1}^{g}\dfrac{c^2_i}{n_i}\right)\dfrac{e_{jj}}{N-g}}\)
and \(e_{jj}\) is the \( \left( j, j \right)^{th}\) element of the error sum of squares and cross products matrix and is equal to the error sums of squares for the analysis of variance of variable j.
Contrast 1
Here we have a \(t_{22,0.005} = 2.819\). The Bonferroni 95% Confidence Intervals are:
| Element | \(\widehat{\Psi}\) | SE( \(\widehat{\Psi}\) ) | \(t\times SE(\widehat{\Psi})\) | Confidence Interval |
|---|---|---|---|---|
| Al | 5.294 | 0.5972 | 1.684 | 3.610, 6.978 |
| Fe | -4.640 | 0.2844 | 0.802 | -5.442, -3.838 |
| Mg | -4.0.65 | 0.3376 | 0.952 | -5.017, -3.113 |
| Ca | -0.175 | 0.0195 | 0.055 | -0.230, -0.120 |
| Na | -0.175 | 0.0384 | 0.108 | -0.283, -0.067 |
Conclusion
Pottery from Ashley Rails and Isle Thorns have higher aluminum and lower iron, magnesium, calcium, and sodium concentrations than pottery from Caldicot and Llanedyrn.
Contrast 3
Bonferroni 95% Confidence Intervals (note: the "M" multiplier below should be the t-value 2.819)
| Element | \(\widehat{\Psi}\) | SE( \(\widehat{\Psi}\) ) | \(M\times SE(\widehat{\Psi})\) | Confidence Interval |
|---|---|---|---|---|
| Al | -0.864 | 1.1199 | 3.157 | -4.021, 2.293 |
| Fe | -0.957 | 0.5333 | 1.503 | -2.460, 0.546 |
| Mg | -0.971 | 0.6331 | 1.785 | -2.756, 0.814 |
| Ca | 0.093 | 0.0366 | 0.103 | -0.010, 0.196 |
| Na | -0.201 | 0.0719 | 0.203 | -0.404, 0.001 |
All resulting intervals cover 0 so there are no significant results.
8.9 - Randomized Block Design: Two-way MANOVA
8.9 - Randomized Block Design: Two-way MANOVAWithin randomized block designs, we have two factors:
- Blocks, and
- Treatments
A randomized complete block design with a treatments and b blocks is constructed in two steps:
- The experimental units (the units to which our treatments are going to be applied) are partitioned into b blocks, each comprised of a units.
- Treatments are randomly assigned to the experimental units in such a way that each treatment appears once in each block.
Randomized block designs are often applied in agricultural settings. The example below will make this clearer.
In general, the blocks should be partitioned so that:
- Units within blocks are as uniform as possible.
- Differences between blocks are as large as possible.
These conditions will generally give you the most powerful results.
Example 8-10: Rice Data (Experimental Design)
Let us look at an example of such a design involving rice.
We have four different varieties of rice; varieties A, B, C, and D. And, we have five different blocks in our study. So, imagine each of these blocks as a rice field or patty on a farm somewhere. These blocks are just different patches of land, and each block is partitioned into four plots. Then we randomly assign which variety goes into which plot in each block. You will note that variety A appears once in each block, as does each of the other varieties. This is how the randomized block design experiment is set up.
| Block 1 | |
|---|---|
| D | C |
| B | A |
| Block 2 | |
|---|---|
| A | D |
| B | C |
| Block 3 | |
|---|---|
| B | D |
| C | A |
| Block 4 | |
|---|---|
| D | B |
| A | C |
| Block 5 | |
|---|---|
| A | C |
| D | B |
A randomized block design with the following layout was used to compare 4 varieties of rice in 5 blocks.
This type of experimental design is also used in medical trials where people with similar characteristics are in each block. This may be people who weigh about the same, are of the same sex, same age, or whatever factor is deemed important for that particular experiment. So generally, what you want is for people within each of the blocks to be similar to one another.
Back to the rice data... In each of the partitions within each of the five blocks, one of the four varieties of rice would be planted. In this experiment, the height of the plant and the number of tillers per plant were measured six weeks after transplanting. Both of these measurements are indicators of how vigorous the growth is. The taller the plant and the greater number of tillers, the healthier the plant is, which should lead to a higher rice yield.
In general, randomized block design data should look like this:
| Block | |||||
|---|---|---|---|---|---|
| 1 | 2 | \(\cdots\) | b | ||
| Treatment 1 | \(\mathbf{Y_{11}} = \begin{pmatrix} Y_{111} \\ Y_{112} \\ \vdots \\ Y_{11p} \end{pmatrix}\) | \(\mathbf{Y_{12}} = \begin{pmatrix} Y_{121} \\ Y_{122} \\ \vdots \\ Y_{12p} \end{pmatrix}\) | \(\cdots\) | \(\mathbf{Y_{1b}} = \begin{pmatrix} Y_{1b1} \\ Y_{1b2} \\ \vdots \\ Y_{1bp} \end{pmatrix}\) | |
| Treatment 2 | \(\mathbf{Y_{21}} = \begin{pmatrix} Y_{211} \\ Y_{212} \\ \vdots \\ Y_{21p} \end{pmatrix}\) | \(\mathbf{Y_{22}} = \begin{pmatrix} Y_{221} \\ Y_{222} \\ \vdots \\ Y_{22p} \end{pmatrix}\) | \(\cdots\) | \(\mathbf{Y_{2b}} = \begin{pmatrix} Y_{2b1} \\ Y_{2b2} \\ \vdots \\ Y_{2bp} \end{pmatrix}\) | |
| Treatment a | \(\mathbf{Y_{a1}} = \begin{pmatrix} Y_{a11} \\ Y_{a12} \\ \vdots \\ Y_{a1p} \end{pmatrix}\) | \(\mathbf{Y_{a2}} = \begin{pmatrix} Y_{a21} \\ Y_{a22} \\ \vdots \\ Y_{a2p} \end{pmatrix}\) | \(\cdots\) | \(\mathbf{Y_{ab}} = \begin{pmatrix} Y_{ab1} \\ Y_{ab2} \\ \vdots \\ Y_{abp} \end{pmatrix}\) | |
We have a rows for the a treatments. In this case, we would have four rows, one for each of the four varieties of rice. We also set up b columns for b blocks. In this case, we have five columns, one for each of the five blocks. In each block, for each treatment, we are going to observe a vector of variables.
Our notation is as follows:
- Let \(Y_{ijk}\) = observation for variable k from block j in treatment i
- We will then collect these into a vector \(\mathbf{Y_{ij}}\) which looks like this:
\(\mathbf{Y_{ij}} = \left(\begin{array}{c}Y_{ij1}\\Y_{ij2}\\\vdots \\ Y_{ijp}\end{array}\right)\)
- a = Number of Treatments
- b = Number of Blocks
8.10 - Two-way MANOVA Additive Model and Assumptions
8.10 - Two-way MANOVA Additive Model and AssumptionsA model is formed for a two-way multivariate analysis of variance.
Two-way MANOVA Additive Model
\(\underset{\mathbf{Y}_{ij}}{\underbrace{\left(\begin{array}{c}Y_{ij1}\\Y_{ij2}\\ \vdots \\ Y_{ijp}\end{array}\right)}} = \underset{\mathbf{\nu}}{\underbrace{\left(\begin{array}{c}\nu_1 \\ \nu_2 \\ \vdots \\ \nu_p \end{array}\right)}}+\underset{\mathbf{\alpha}_{i}}{\underbrace{\left(\begin{array}{c} \alpha_{i1} \\ \alpha_{i2} \\ \vdots \\ \alpha_{ip}\end{array}\right)}}+\underset{\mathbf{\beta}_{j}}{\underbrace{\left(\begin{array}{c}\beta_{j1} \\ \beta_{j2} \\ \vdots \\ \beta_{jp}\end{array}\right)}} + \underset{\mathbf{\epsilon}_{ij}}{\underbrace{\left(\begin{array}{c}\epsilon_{ij1} \\ \epsilon_{ij2} \\ \vdots \\ \epsilon_{ijp}\end{array}\right)}}\)
In this model:
- \(\mathbf{Y}_{ij}\) is the p × 1 vector of observations for treatment i in block j;
This vector of observations is written as a function of the following
- \(\nu_{k}\) is the overall mean for variable k; these are collected into the overall mean vector \(\boldsymbol{\nu}\)
- \(\alpha_{ik}\) is the effect of treatment i on variable k; these are collected into the treatment effect vector \(\boldsymbol{\alpha}_{i}\)
- \(\beta_{jk}\) is the effect of block j on variable k; these are collected in the block effect vector \(\boldsymbol{\beta}_{j}\)
- \(\varepsilon_{ijk}\) is the experimental error for treatment i, block j, and variable k; these are collected into the error vector \(\boldsymbol{\varepsilon}_{ij}\)
Assumptions
These are fairly standard assumptions with one extra one added.
- The error vectors \(\varepsilon_{ij}\) have zero population mean;
- The error vectors \(\varepsilon_{ij}\) have a common variance-covariance matrix \(\Sigma\) — (the usual assumption of a homogeneous variance-covariance matrix)
- The error vectors \(\varepsilon_{ij}\) are independently sampled;
- The error vectors \(\varepsilon_{ij}\) are sampled from a multivariate normal distribution;
- There is no block-by-treatment interaction. This means that the effect of the treatment is not affected by, or does not depend on the block.
These are the standard assumptions.
We could define the treatment mean vector for treatment i such that:
\(\mu_i = \nu +\alpha_i\)
Here we could consider testing the null hypothesis that all of the treatment mean vectors are identical,
\(H_0\colon \boldsymbol{\mu_1 = \mu_2 = \dots = \mu_g}\)
or equivalently, the null hypothesis that there is no treatment effect:
\(H_0\colon \boldsymbol{\alpha_1 = \alpha_2 = \dots = \alpha_a = 0}\)
This is the same null hypothesis that we tested in the One-way MANOVA.
We would test this against the alternative hypothesis that there is a difference between at least one pair of treatments on at least one variable, or:
\(H_a\colon \mu_{ik} \ne \mu_{jk}\) for at least one \(i \ne j\) and at least one variable \(k\)
We will use standard dot notation to define mean vectors for treatments, mean vectors for blocks, and a grand mean vector.
We define a mean vector for treatment i:
\(\mathbf{\bar{y}}_{i.} = \frac{1}{b}\sum_{j=1}^{b}\mathbf{Y}_{ij} = \left(\begin{array}{c}\bar{y}_{i.1}\\ \bar{y}_{i.2} \\ \vdots \\ \bar{y}_{i.p}\end{array}\right)\) = Sample mean vector for treatment i.
In this case, it is comprised of the mean vectors for ith treatment for each of the p variables and it is obtained by summing over the blocks and then dividing by the number of blocks. The dot appears in the second position indicating that we are to sum over the second subscript, the position assigned to the blocks.
For example, \(\bar{y}_{i.k} = \frac{1}{b}\sum_{j=1}^{b}Y_{ijk}\) = Sample mean for variable k and treatment i.
We define a mean vector for block j:
\(\mathbf{\bar{y}}_{.j} = \frac{1}{a}\sum_{i=1}^{a}\mathbf{Y}_{ij} = \left(\begin{array}{c}\bar{y}_{.j1}\\ \bar{y}_{.j2} \\ \vdots \\ \bar{y}_{.jp}\end{array}\right)\) = Sample mean vector for block j.
Here we will sum over the treatments in each of the blocks so the dot appears in the first position. Therefore, this is essentially the block means for each of our variables.
For example, \(\bar{y}_{.jk} = \frac{1}{a}\sum_{i=1}^{a}Y_{ijk}\) = Sample mean for variable k and block j.
Finally, we define the Grand mean vector by summing all of the observation vectors over the treatments and the blocks. So you will see the double dots appearing in this case:
\(\mathbf{\bar{y}}_{..} = \frac{1}{ab}\sum_{i=1}^{a}\sum_{j=1}^{b}\mathbf{Y}_{ij} = \left(\begin{array}{c}\bar{y}_{..1}\\ \bar{y}_{..2} \\ \vdots \\ \bar{y}_{..p}\end{array}\right)\) = Grand mean vector.
This involves dividing by a × b, which is the sample size in this case.
For example, \(\bar{y}_{..k}=\frac{1}{ab}\sum_{i=1}^{a}\sum_{j=1}^{b}Y_{ijk}\) = Grand mean for variable k.
As before, we will define the Total Sum of Squares and Cross Products Matrix. This is the same definition that we used in the One-way MANOVA. It involves comparing the observation vectors for the individual subjects to the grand mean vector.
\(\mathbf{T = \sum_{i=1}^{a}\sum_{j=1}^{b}(Y_{ij}-\bar{y}_{..})(Y_{ij}-\bar{y}_{..})'}\)
Here, the \( \left(k, l \right)^{th}\) element of T is
\(\sum_{i=1}^{a}\sum_{j=1}^{b}(Y_{ijk}-\bar{y}_{..k})(Y_{ijl}-\bar{y}_{..l}).\)
- For \( k = l \), this is the total sum of squares for variable k and measures the total variation in variable k.
- For \( k ≠ l \), this measures the association or dependency between variables k and l across all observations.
In this case, the total sum of squares and cross products matrix may be partitioned into three matrices, three different sums of squares cross-product matrices:
\begin{align} \mathbf{T} &= \underset{\mathbf{H}}{\underbrace{b\sum_{i=1}^{a}\mathbf{(\bar{y}_{i.}-\bar{y}_{..})(\bar{y}_{i.}-\bar{y}_{..})'}}}\\&+\underset{\mathbf{B}}{\underbrace{a\sum_{j=1}^{b}\mathbf{(\bar{y}_{.j}-\bar{y}_{..})(\bar{y}_{.j}-\bar{y}_{..})'}}}\\ &+\underset{\mathbf{E}}{\underbrace{\sum_{i=1}^{a}\sum_{j=1}^{b}\mathbf{(Y_{ij}-\bar{y}_{i.}-\bar{y}_{.j}+\bar{y}_{..})(Y_{ij}-\bar{y}_{i.}-\bar{y}_{.j}+\bar{y}_{..})'}}} \end{align}
As shown above:
- H is the Treatment Sum of Squares and Cross Products matrix;
- B is the Block Sum of Squares and Cross Products matrix;
- E is the Error Sum of Squares and Cross Products matrix.
The \( \left(k, l \right)^{th}\) element of the Treatment Sum of Squares and Cross Products matrix H is
\(b\sum_{i=1}^{a}(\bar{y}_{i.k}-\bar{y}_{..k})(\bar{y}_{i.l}-\bar{y}_{..l})\)
- If \(k = l\), is the treatment sum of squares for variable k, and measures variation between treatments.
- If \( k ≠ l \), this measures how variables k and l vary together across treatments.
The \( \left(k, l \right)^{th}\) element of the Block Sum of Squares and Cross Products matrix B is
\(a\sum_{j=1}^{a}(\bar{y}_{.jk}-\bar{y}_{..k})(\bar{y}_{.jl}-\bar{y}_{..l})\)
- For \( k = l \), is the block sum of squares for variable k, and measures variation between or among blocks.
- For \( k ≠ l \), this measures how variables k and l vary together across blocks (not usually of much interest).
The \( \left(k, l \right)^{th}\) element of the Error Sum of Squares and Cross Products matrix E is
\(\sum_{i=1}^{a}\sum_{j=1}^{b}(Y_{ijk}-\bar{y}_{i.k}-\bar{y}_{.jk}+\bar{y}_{..k})(Y_{ijl}-\bar{y}_{i.l}-\bar{y}_{.jl}+\bar{y}_{..l})\)
- For \( k = l \), is the error sum of squares for variable k, and measures variability within treatment and block combinations of variable k.
- For \( k ≠ l \), this measures the association or dependence between variables k and l after you take into account treatment and block.
8.11 - Forming a MANOVA table
8.11 - Forming a MANOVA tableThe partitioning of the total sum of squares and cross products matrix may be summarized in the multivariate analysis of variance table as shown below:
| Source | d.f. | SSP |
|---|---|---|
| Blocks | b - 1 | B |
| Treatments | a - 1 | H |
| Error | (a - 1)(b - 1) | E |
| Total | ab - 1 | T |
SSP stands for the sum of squares and cross products discussed above.
To test the null hypothesis that the treatment mean vectors are equal, compute a Wilks Lambda using the following expression:
\(\Lambda^* = \dfrac{|\mathbf{E}|}{|\mathbf{H+E}|}\)
This is the determinant of the error sum of squares and cross-products matrix divided by the determinant of the sum of the treatment sum of squares and cross-products plus the error sum of squares and cross-products matrix.
Under the null hypothesis, this has an F-approximation. The approximation is quite involved and will not be reviewed here. Instead, let's take a look at our example where we will implement these concepts.
Example 8-11: Rice Data
Rice data can be downloaded here: rice.csv
The program below shows the analysis of the rice data.
Download the SAS Program here: rice.sas
Note: In the upper right-hand corner of the code block you will have the option of copying ( ) the code to your clipboard or downloading ( ) the file to your computer.
options ls=78;
title "Two-Way MANOVA: Rice Data";
data rice;
infile "D:\Statistics\STAT 505\data\rice.csv" firstobs=2 delimiter=',';
input block variety $ height tillers;
run;
/*
* The class statement specifies block and variety as categorical variables.
* The model statement specifies responses height and tillers with predictors
* block and variety. lsmeans displays the least-squares means for variety.
* The manova statement requests the test for response mean vectors across
* levels of variety, and the printe and printh options display sums of
* squares and cross products for error and the hypothesis, respectively.
*/
proc glm data=rice;
class block variety;
model height tillers=block variety;
lsmeans variety;
manova h=variety / printe printh;
run;
Performing a two-way MANOVA
To carry out the two-way MANOVA test in Minitab:
- Open the ‘rice’ data set in a new worksheet.
- For convenience, rename the columns: block, variety, height, and tillers, from left to right.
- Stat > ANOVA > General MANOVA
- Highlight and select height and tillers to move them to the Responses window.
- Highlight and select block and variety to move them to the Model window.
- Choose 'OK'. The MANOVA results for the tests for block and variety are separately displayed in the results area.
Analysis
- We reject the null hypothesis that the variety mean vectors are identical \(( \Lambda = 0.342; F = 2.60 ; d f = 6,22 ; p = 0.0463 )\). At least two varieties differ in means for height and/or number of tillers.
- Results of the ANOVAs on the individual variables:
Variable F SAS p-value Bonferroni p-value Height 4.19 0.030 0.061 Tillers 1.27 0.327 0.654 Each test is carried out with 3 and 12 d.f. Because we have only 2 response variables, a 0.05 level test would be rejected if the p-value is less than 0.025 under a Bonferroni correction. Thus, if a strict \(α = 0.05\) level is adhered to, then neither variable shows a significant variety effect. However, if a 0.1 level test is considered, we see that there is weak evidence that the mean heights vary among the varieties (F = 4.19; d. f. = 3, 12).
- The Mean Heights are presented in the following table:
Variety Mean Standard Error A 58.4 1.62 B 50.6 1.62 C 55.2 1.62 D 53.0 1.62 -
Variety A is the tallest, while variety B is the shortest. The standard error is obtained from:
\(SE(\bar{y}_{i.k}) = \sqrt{\dfrac{MS_{error}}{b}} = \sqrt{\dfrac{13.125}{5}} = 1.62\)
- Looking at the partial correlation (found below the error sum of squares and cross-products matrix in the output), we see that height is not significantly correlated with the number of tillers within varieties \(( r = - 0.278 ; p = 0.3572 )\).
8.12 - Summary
8.12 - SummaryIn this lesson we learned about:
- The 1-way MANOVA for testing the null hypothesis of equality of group mean vectors;
- Methods for diagnosing the assumptions of the 1-way MANOVA;
- Bonferroni corrected ANOVAs to assess the significance of individual variables;
- Construction and interpretation of orthogonal contrasts;
- Wilks lambda for testing the significance of contrasts among group mean vectors; and
- Simultaneous and Bonferroni confidence intervals for the elements of contrast.
In general, a thorough analysis of data would be comprised of the following steps:
-
Step 1:
Perform appropriate diagnostic tests for the assumptions of the MANOVA. Carry out appropriate normalizing and variance-stabilizing transformations of the variables.
-
Step 2:
Perform a one-way MANOVA to test for equality of group mean vectors. If this test is not significant, conclude that there is no statistically significant evidence against the null hypothesis that the group mean vectors are equal to one another and stop. If the test is significant, conclude that at least one pair of group mean vectors differ on at least one element and go on to Step 3.
-
Step 3:
Perform Bonferroni-corrected ANOVAs on the individual variables to determine which variables are significantly different among groups.
-
Step 4:
Construct up to g-1 orthogonal contrasts based on specific scientific questions regarding the relationships among the groups.
-
Step 5:
Use Wilks lambda to test the significance of each contrast defined in Step 4.
-
Step 6:
For the significant contrasts only, construct simultaneous or Bonferroni confidence intervals for the elements of those contrasts. Draw appropriate conclusions from these confidence intervals, making sure that you note the directions of all effects (which treatments or group of treatments have the greater means for each variable).
In this lesson we also learned about:
- How to perform multiple factor MANOVAs;
- What conclusions may be drawn from the results of a multiple-factor MANOVA;
- The Bonferroni corrected ANOVAs for the individual variables.
Just as in the one-way MANOVA, we carried out orthogonal contrasts among the four varieties of rice. However, in this case, it is not clear from the data description just what contrasts should be considered. If a phylogenetic tree were available for these varieties, then appropriate contrasts may be constructed.