Lesson 6: Sample Size and Power - Part a
Lesson 6: Sample Size and Power - Part aOverview
The underlying theme of sample size calculation in all clinical trials is precision. ; Validity and unbiasedness do not necessarily relate to sample size.
Usually, sample size is calculated with respect to two circumstances. The first involves precision for an estimator, e.g., requiring a 95% confidence interval for the population mean to be within ± \(\delta\) units. The second involves statistical power for hypothesis testing, e.g., requiring 0.80 or 0.90 statistical power \(\left(1- \beta\right)\) for a hypothesis test when the significance level (\(\alpha\)) is 0.05 and the effect size (the clinically meaningful effect) is \(\Delta\) units.
The formulae for many sample size calculations will involve percentiles from the standard normal distribution. The graph below illustrates the 2.5th percentile and the 97.5th percentile.
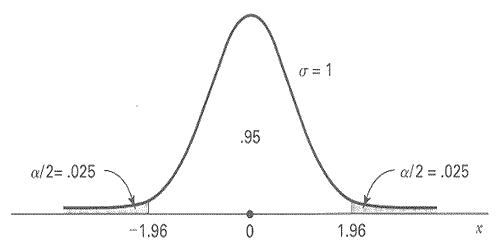
Fig. 1 Standard normal distribution centered on zero.
For a two-sided hypothesis test with significance level α and statistical power \(1 - \beta\), the percentiles of interest are \(z_{(1-\alpha/2)}\) and \(z_{(1 - \beta)}\).
For a one-sided hypothesis test, \(z_{(1 - \alpha)}\) is used instead. Usual choices of \(\alpha\) are 0.05 and 0.01, and usual choices of \(\beta\) are 0.20 and 0.10, so the percentiles of interest usually are:
\( z_{0.995} = 2.58, z_{0.99} = 2.33, z_{0.975} = 1.96, z_{0.95} = 1.65, z_{0.90} = 1.28, z_{0.80} = 0.84 \).
In SAS, the PROBIT function is available to generate percentiles from the standard normal distribution function, e.g., Z = PROBIT(0.99) yields a value of 2.33 for Z. So, if you ever need to generate z-values you can get SAS to do this for you.
It is important to realize that sample size calculations are approximations. The assumptions that are made for the sample size calculation, e.g., the standard deviation of an outcome variable or the proportion of patients who succeed with placebo, may not hold exactly.
Also, we may base the sample size calculation on a t statistic for a hypothesis test, which assumes an exact normal distribution of the outcome variable when it only may be approximately normal.
In addition, there will be loss-to-follow-up, so not all of the subjects who initiate the study will provide complete data. .Some will deviate from the protocol, including not taking the assigned treatment or adding on a treatment. Sample size calculations and recruitment of subjects should reflect these anticipated realities.
Objectives
- Identify studies for which sample size is an important issue.
- Estimate the sample size required for a confidence interval for p for given \(\delta\) and \(\alpha\), using normal approximation and Fisher's exact methods.
- Estimate the sample size required for a confidence interval for \(\mu\) for given \(\delta\) and \(\alpha\), using normal approximation when the sample size is relatively large.
- Estimate the sample size required for a test of \(H_0 \colon \mu_{1} = \mu_{2}\) to have \(\left(1-\beta\right)\%\) power for given \(\delta\) and \(\alpha\), using normal approximation, with equal or unequal allocation.
- Estimate the sample size required for a test of \(H_0 \colon p_{1} = p_{2}\) for given \(\delta\) and \(\alpha\) and \(\beta\), using normal approximation and Fisher's exact methods.
- Use a SAS program to estimate the number of events required for a logrank comparison of two hazard functions to have \(\left(1-\beta\right)\%\) power with given \(\alpha\)
- Use Poisson probability methods to determine the cohort size required to have a certain probability of detecting a rare event that occurs at a rate = ξ.
- Adjust sample size requirements to account for multiple comparisons and the anticipated withdrawal rate.
Reference:
Friedman, Furberg, DeMets, Reboussin and Granger. (2015) Sample size. In: FFDRG. Fundamentals of Clinical Trials. 5th ed. Switzerland: Springer.
Piantadosi Steven. (2005) Sample size and power. In: Piantadosi Steven. Clinical Trials: A Methodologic Perspective. 2nd ed. Hoboken, NJ: John Wiley and Sons, Inc.
Wittes, Janet. (2002) "Sample Size Calculations for Randomized Controlled Trials." Epidemiologic Reviews. Vol. 24. No 1. pp. 39-53.
6a.1 - Treatment Mechanism and Dose Finding Studies
6a.1 - Treatment Mechanism and Dose Finding StudiesFor many treatment mechanism (TM) studies, sample size is not an important issue because usually only a few subjects are enrolled to investigate treatment mechanisms. Here you are taking a lot of measurements on a few subjects in order to find out what might be going on with your treatment.
As presented last week, dose-finding (DF) and dose-ranging studies typically involve a design scheme, such as a modified Fibonacci design or continual reassessment. An example of phase I cytotoxic drug trials is as follows. A set of doses is determined a priori, such as 100 mg, 200 mg, 300 mg, 500 mg, 800 mg, etc. Subjects are recruited into the DF study in groups of three. The first group receives the lowest dose of 100 mg. If none of the subjects experience the effect (toxicity, side effect, etc.), then the next group of three subjects is escalated to the next dose of 200 mg. If one of the three subjects at 100 mg experiences the effect, however, then the next group of three subjects will receive the same dose of 100 mg. Whenever six subjects at the same dose reveal at least two subjects that experience the effect, then the study is terminated and the chosen dose for a safety and efficacy study is the previous dose level.
With such mechanisms in place to determine initial dosage levels, selection of. the study sample size is not a major consideration. In fact, the final sample size is dependent on patient outcomes.
6a.2 - Safety and Efficacy Studies
6a.2 - Safety and Efficacy StudiesThe U.S. FDA mandates that efficacy is proven prior to the approval of a drug. Efficacy means that the tested dose of the drug is effective at ameliorating the treated condition. Phase II trials evaluate the potential for efficacy; Phase III trials confirm efficacy. These trials can also be referred to as safety and activity studies.
A typical goal of a safety and efficacy (SE) study is to estimate certain clinical endpoints with a specified amount of precision. Confidence intervals are useful for reflecting the amount of precision, and the width of a confidence interval is a function of sample size.
The simplest example occurs when the outcome response is binary (success or failure). Let p denote the true (but unknown) proportion of successes in the population that will be estimated from a sample.
The sample size is denoted as n and the number of observed successes is r. Thus, the point estimate of p is:
\(\hat{p}=\frac{r}{n}\)
If the sample size is large enough, then the \(100(1 - \alpha)\%\) confidence interval can be approximated as:
\( \hat{p}\pm z_{1-\alpha/2}\sqrt{\hat{p}(1-\hat{p})/n}\)
Prior to the conduct of the study, however, the point estimate is undetermined so that an educated guess is necessary for the purposes of a sample size calculation.
If it is desirable for the confidence interval to have limits of \( \hat{p} \pm \delta \) .
for a \(100(1 - \alpha)\%\) confidence interval, and the researcher has a reasonable guess as to the value of p, reworking through the sample size equation, the target sample size is:
\( n=z_{1-\alpha/2}^{2}p(1-p)/\delta^2 \)
If a researcher guesses that \(p ≈ 0.4\) and wants a 95% confidence interval to have limits of \(\delta = 0.10\), then the required sample size is
\(n = \dfrac{(1.96)^{2}(0.4)(0.6)}{(0.10)^2} = 92\)
Notice that \(p(1 - p)\) is maximized when \(p = 0.5\). Therefore, because p has to be guessed, it is more conservative to use p = 0.5 in the sample size calculation. In the above example this yields \(n = \dfrac{(1.96)^2(0.5)(0.5)}{(0.10)^2} = 96\), a slightly larger sample size.
Notice that the sample size is a quadratic function of precision. If \(\delta = 0.05\) is desired instead of 0.10 in the above example, then
\(n = \dfrac{(1.96)^2(0.5)(0.5)}{(0.05)^2} = 384\)
If you want the confidence interval to be tighter remember that splitting the width of the confidence interval in half will involve quadrupling the number of subjects in the sample size!
The normal approximation for calculating the \(100(1 - \alpha)\%\) confidence for p works well if
\( n \hat{p}\left(1-\hat{p}\right) \ge 5 \)
Otherwise, exact binomial methods should be used.
In the exact binomial method, the lower \(100(\alpha/2)\%\) confidence limit for \(p\) is determined as the value \(p_L\) that satisfies
\(\alpha/2=\sum_{k=r}^{n}C(n,k)\ast (p_L)^k(1-p_L)^{n-k} \)
The upper \(100(1 - \alpha/2)\%\) confidence limit for \(p\) is determined as the value \(p_U\) that satisfies
\(\alpha/2=\sum_{k=0}^{r}C(n,k)\ast (p_U)^k(1-p_U)^{n-k} \)
SAS PROC FREQ provides the exact and asymptotic \(100(1 - \alpha)\%\) confidence intervals for a binomial proportion, p.
SAS® Example
Using PROC FREQ in SAS for determining an exact confidence interval for a binomial proportion
6.1_binomial_proportion.sas (from Piantadosi, 2005) This is a program that illustrates the use of PROC FREQ in SAS for determining an exact confidence interval for a binomial proportion.
***********************************************************************
* This is a program that illustrates the use of PROC FREQ in SAS for *
* determining an exact confidence interval for a binomial proportion. *
***********************************************************************;
proc format;
value succfmt 1='yes' 2='no';
run;
data Example_1;
input success count;
format success succfmt.;
cards;
1 03
2 16
;
run;
proc freq data=Example_1;
tables success/binomial alpha=0.05;
weight count/zeros;
title "Exact and Asymptotic 95% Confidence Intervals for a Binomial Proportion";
run;
In the example above, \(n = 19\) is the sample size and \(r = 3\) successes are observed in a binomial trial. The point estimate of p is
\( \hat{p} = 0.16 \)
Note, however, that
\( n\hat{p}(1-\hat{p}) = 19(0.16)(0.84)=2.55 <5 \)
The 95% confidence interval for p, based on the exact method, is [0.03, 0.40]. The 95% confidence interval for p, based on the normal approximation, is [-0.01, 0.32], which is modified to [0.00, 0.32] because p represents the probability of success that is supposed to be restricted to lie within the [0, 1] interval. Even with the correction to the lower endpoint, the confidence interval based on the normal approximation does not appear to be very accurate in this example.
Now it's your turn!
Modify the SAS program above to reflect 11 successes out of 75 trials. Run the program. Do the results round to (0.08, 0.25) for the 95% exact confidence limits?
If an investigator estimates \(p = 0.15\) and wants a 95% exact confidence interval with \(\delta = 0.1\), what sample size is needed? One way to solve this is to use SAS PROC FREQ in a "guess and check" manner. In this case, \(n = 73\) with 11 successes will result in a 95% exact confidence interval of (0.07, 0.25). It may impossible to exactly achieve the desired \(\delta\), but an estimate of the required sample size can be provided.
Using the exact confidence interval for a binomial proportion is the better option if you are not sure you are working in a standard normally distributed population.
6a.3 - Example: Discarding Ineffective Treatment
6a.3 - Example: Discarding Ineffective TreatmentAn approach for discarding an ineffective treatment in an SE study, based on the exact binomial method, is as follows. Suppose that the lowest success rate acceptable to an investigator for the treatment is 0.20. Suppose that the investigator decides to administer the treatment consecutively to a series of patients. When can the investigator terminate the SE trial if he continues to find no treatment successes?
SAS® Example
Determine when the exact confidence interval for p no longer contains a certain value
SAS Example: Modifications to the exact confidence interval program used earlier can be made to determine when the exact confidence interval for p no longer contains a certain value.
***********************************************************************
* This is a program that illustrates the use of PROC FREQ in SAS for *
* determining an exact confidence interval for a binomial proportion. *
***********************************************************************;
proc format;
value succfmt 1='yes' 2='no';
run;
data Example_1;
input success count;
format success succfmt.;
cards;
1 03
2 16
;
run;
proc freq data=Example_1;
tables success/binomial alpha=0.05;
weight count/zeros;
title "Exact and Asymptotic 95% Confidence Intervals for a Binomial Proportion";
run;
SAS PROF FREQ (trial-and-error) indicates that the exact one-sided 95% upper confidence limit for p, when 0 out of 14 successes are observed, is 0.19. Thus, if the treatment fails in each of the first 14 patients, then the study is terminated.
Did you get 45% with the exact limits?
Notice also how clearly wrong the asymptotic limit is in this situation.
| The FREQ Procedure | ||||
|---|---|---|---|---|
| Positive | Frequency | Percent | Cumulative Frequency | Cumulative Percent |
| yes | 0 | 0.00 | 0 | 0.00 |
| no | 5 | 100.00 | 5 | 100.00 |
|
Binomial Proportion |
|
|---|---|
| Proportion | 0.0000 |
| ASE | 0.0000 |
| 90% Lower Conf Limit | 0.0000 |
| 90% Upper Conf Limit | 0.0000 |
| Exact Conf Limits | |
| 90% Lower Conf Limit | 0.0000 |
| 90% Upper Conf Limit | 0.4507 |
|
Test of H0: Proportion = 0.5 |
|
|---|---|
| ASE Under H0 | 0.2236 |
| Z | -2.2361 |
| One-Sided Pr < Z | 0.0127 |
| Two-Sided Pr > |Z| | 0.0253 |
Sample Size = 5
The answer is 9 ...
| The FREQ Procedure | ||||
|---|---|---|---|---|
| Positive | Frequency | Percent | Cumulative Frequency | Cumulative Percent |
| yes | 0 | 0.00 | 0 | 0.00 |
| no | 9 | 100.00 | 9 | 100.00 |
|
Binomial Proportion |
|
|---|---|
| Proportion | 0.0000 |
| ASE | 0.0000 |
| 90% Lower Conf Limit | 0.0000 |
| 90% Upper Conf Limit | 0.0000 |
| Exact Conf Limits | |
| 90% Lower Conf Limit | 0.0000 |
| 90% Upper Conf Limit | 0.2831 |
|
Test of H0: Proportion = 0.5 |
|
|---|---|
| ASE Under H0 | 0.1667 |
| Z | -3.0000 |
| One-Sided Pr < Z | 0.0013 |
| Two-Sided Pr > |Z| | 0.0027 |
Sample Size = 9
6a.4 - Confidence Intervals for Means
6a.4 - Confidence Intervals for MeansFor a clinical endpoint that can be approximated by a normal distribution in an SE study, the \(100(1 - \alpha)\%\) confidence interval for the population mean, \(\mu\), is
\( \bar{Y} \pm \left [ t_{n-1, 1-\alpha/2}s/\sqrt{n} \right ] \)
where
\( \bar{Y}=\sum_{i=1}^{n}Y_i/n \) is the sample mean,
\( t_{n-1, 1-\alpha/2} \) is the appropriate percentile from the \(t_{n-1}\) distribution, and
\( s^2= \sum_{i=1}^{n}(Y_{i} - \bar{Y})^2 / (n-1) \) is the sample variance and estimates \(σ^{2}\).
If σ is known, then a z-percentile can replace the t-percentile in the \(100(1 - \alpha)\%\) confidence interval for the population mean, \(\mu\), that is,
\( \bar{Y} \pm \left( z_{1- \alpha /2}\sigma / \sqrt{n} \right) \)
If n is relatively large, say n ≥ 60, then \(z_{1 - \alpha/2} ≈ t_{n - 1,1 - \alpha/2}\).
If it is desired for the \(100(1 - \alpha)\%\) confidence interval to be
\( \bar{Y} \pm \delta \)
then
\( n= z_{1-\alpha/2}^{2}\sigma^2/\delta^2 \)
For example, the necessary sample size for estimating the mean reduction in diastolic blood pressure, where \(σ = 5\) mm Hg and \(δ = 1\) mm Hg, is \(n = \dfrac{1.96^{2} \times 5^{2}}{1^2} = 96\).
6a.5 - Comparative Treatment Efficacy Studies
6a.5 - Comparative Treatment Efficacy StudiesSuppose that a comparative treatment efficacy (CTE) trial consists of comparing two independent treatment groups with respect to the means of the primary clinical endpoint. Let \(\mu_1\) and \(\mu_2\) denote the unknown population means of the two groups, and let \(\sigma\) denote the known standard deviation common to both groups. Also, let \(n_1\) and \(n_2\) denote the sample sizes of the two groups.
The treatment difference in means is \(\Delta = \mu_1 -\mu_2\) and the null hypothesis is \(H_0\colon \Delta = 0\). The test statistic is
\( Z = \left( \bar{Y}_1 - \bar{Y}_2 \right) / \sigma \sqrt{\frac{1}{n_1}+\frac{1}{n_2}} \)
which follows a standard normal distribution when the null hypothesis is true. If the alternative hypothesis is two-sided, i.e., \(H_1 \colon \Delta \ne 0\), then the null hypothesis is rejected for large values of |Z|.
Under a particular alternative where there might be some difference \(\Delta, \Delta = \mu_1 - \mu_2\),
\( Z = \left( \bar{Y}_1 - \bar{Y}_2 - \Delta \right)/ \sigma \sqrt{\frac{1}{n_1}+\frac{1}{n_2}} \)
Suppose we let \(AR = \dfrac{n_1}{n_2}\) denote the allocation ratio \(\left(AR\right)\), (in most cases we will assign \(AR = 1\) to get equal sample sizes). If we wish to a have large enough sample size to detect an effect size Δ with a two-sided, α-significance level test with \(100 \left(1 - \beta \right)\%\) statistical power, then
\( n_2 = \left( \frac{AR+1}{AR}\right) \left( z_{1-\alpha/2}+z_{1-\beta} \right)^2\sigma^2/\Delta^2 \)
and \(n_1 = AR \times n_2\).
Note this formula matches the sample size formula in our FFDRG text on p. 180, assuming equal allocation to the two treatment groups and multiplying the result here by 2 to get 2N, which FFDRG uses to denote the total sample size.
If the alternative hypothesis is one-sided, then \(Z_{1 - α}\) replaces \(Z_{1 - \frac{\alpha}{2}}\) in either formula.
Notice that the sample size expression contains \(\left(\dfrac{\sigma}{\Delta}\right)^2\), the square of the effect size expressed in standard deviation units. Thus, sample size is a quadratic function of the effect size and precision. As the variance gets larger, it has a quadratic effect on the sample size. For example, reducing the effect size by one-half quadruples the required sample size.
Although this sample size formula assumes that the standard deviation is known so that a z test can be applied, it works relatively well when the standard deviation must be estimated and a t-test applied. A preliminary guess of σ must be available, however, either from a small pilot study or a report in the literature. For smaller sample sizes \(\left(n_1 ≤ 30, n_2 ≤ 30 \right)\) percentiles from a t distribution can be substituted, although this results in both sides of the formula involving \(n_2\) so that it must be solved iteratively:
\( n_2 = \left( \dfrac{AR+1}{AR}\right) \left( t_{n_1+n_2-2,1-\alpha/2}+t_{n_1+n_2-2,1-\beta} \right)^2\sigma^2/\Delta^2 \)
6a.6 - Example: Comparative Treatment Efficacy Studies
6a.6 - Example: Comparative Treatment Efficacy StudiesSAS® Example
Using PROC POWER to calculate sample size when comparing two normal means
An investigator wants to determine the sample size for comparing two asthma therapies with respect to the forced expiratory volume in one second \(\left(FEV_1\right)\). A two-sided, 0.05-significance level test with 90% statistical power is desired. The effect size is \(\Delta = 0.25 \text{ L}\) and the standard deviation reported in the literature for a similar population is \(\sigma = 0.75 \text{ L}\). The investigator plans to have equal allocation to the two treatment groups (AR = 1).
The first step is to identify the primary response variable. In this example, \(FEV_1\) is a continuous response variable. Assuming that \(FEV_1\) has an approximate normal distribution, the number of patients required for the second treatment group based on the z formula is
\(n_2 = \dfrac{(2)(1.96 + 1.28)^2(0.75)^2}{(0.25)^2 } = 189\)
Thus, the total sample size required is \(n_1 + n_2 = 189 + 189 = 378\). SAS Example: This is a program that illustrates the use of PROC POWER to calculate sample size when comparing two normal means.
***********************************************************************
* This is a program that illustrates the use of PROC POWER to *
* calculate sample size when comparing two normal means. *
***********************************************************************;
proc power;
twosamplemeans dist=normal groupweights=(1 1) alpha=0.05 power=0.9 stddev=0.75
meandiff=0.25 test=diff sides=2 ntotal=.;
plot min=0.1 max=0.9;
title "Sample Size Calculation for Comparing Two Normal Means (1:1 Allocation)";
run;
proc power;
twosamplemeans dist=normal groupweights=(2 1) alpha=0.05 power=0.9 stddev=0.75
meandiff=0.25 test=diff sides=2 ntotal=.;
plot min=0.1 max=0.9;
title "Sample Size Calculation for Comparing Two Normal Means (2:1 Allocation)";
run;
SAS PROC POWER, based on the t formula, yields \(n_1 + n_2 = 191 + 191 = 382\).
If the investigator had wanted an allocation ratio of \(AR = 2\) (twice as many subjects in the first group), then \(n_2 = \dfrac{(1.5)(1.96 + 1.28)^2(0.75)^2}{(0.25)^2} = 142\) and \(n_1 = 2 \times 142 = 284\).
The total sample size required is \(n_1 + n_2 = 142 + 284 = 426\).
SAS PROC POWER, based on the t formula, yields \(n_1 + n_2 = 143 + 286 = 429\).
Notice that the 2:1 allocation, when compared to the 1:1 allocation, requires an overall larger sample size (429 versus 382).
Now it is your turn to give it a try!
Try it!
144 subjects
Here is the output that you should have obtained ...
|
The POWER Procedure |
|
|---|---|
| Fixed Scenario Elements | |
| Distribution | Normal |
| Method | Exact |
| Number of Sides | 2 |
| Alpha | 0.05 |
| Mean Difference | 5 |
| Standard Deviation | 10 |
| Group 1 Weight | 2 |
| Group 2 Weight | 1 |
| Nominal Power | 0.8 |
| Null Difference | 0 |
| Computed N Total | |
|---|---|
| Actual Power | N Total |
| 0.802 | 144 |
6a.7 - Example: Comparative Treatment Efficacy Studies
6a.7 - Example: Comparative Treatment Efficacy StudiesWhat if the primary response variable is binary?
When the outcome in a CTE trial is a binary response and the objective is to compare the two groups with respect to the proportion of success, the results can be expressed in a 2 × 2 table as
| Group # 1 | Group # 2 | |
| Success | \(r_1\) | \(r_2\) |
| Failure | \(n_1 - r_1\) | \(n_2 - r_2\) |
There are a variety of methods for performing the statistical test of the null hypothesis \(H_0\colon p_1 = p_2\), such as a z-test using a normal approximation, a \(χ^2\) test (basically, a square of the z-test), a \(χ^2\) test with continuity correction, and Fisher's exact test.
The normal and \(χ^2\) approximations for comparing two proportions are relatively accurate when these conditions are met:
\( \dfrac{n_1(r_1+r_2)}{(n_1+n_2}\ge 5, \dfrac{n_2(r_1+r_2)}{(n_1+n_2}\ge 5, \dfrac{n_1(n_1+n_2-r_1-r_2)}{(n_1+n_2}\ge 5, \dfrac{n_2(n_1+n_2-r_1-r_2)}{(n_1+n_2}\ge 5 \)
Basically when the expected number in each cell is greater than 5, the normal or Chi Square approximation is useful.
Otherwise, Fisher's exact test is recommended. All of these tests are available in SAS PROC FREQ of SAS and will be discussed later in the course.
A sample size formula for comparing the proportions \(p_1\) and \(p_2\) using the normal approximation is given below:
\( n_2=\left( \dfrac{AR+1}{AR}\right)\left( z_{1-\alpha/2}+z_{1-\beta}\right)^2\bar{p}(1-\bar{p})/(p_1-p_2)^2 \)
where \(p_1 - p_2\) represents the effect size and
\( \bar{p}= (AR \cdot p_1+p_2) / (AR+1) \)
is the weighted average of the proportions.
SAS® Example
Using PROC POWER to calculate sample size when comparing two binomial proportions
An investigator wants to compare an experimental therapy to placebo when the response is success/failure via a two-sided, 0.05 significance level test and 90% statistical power. She knows from the medical literature that 25% of the untreated patients will experience success, so she decides that the experimental therapy is worthwhile if it can yield a 50% success rate. With equal allocation, \(n_2 = \dfrac{(2)(1.96 + 1.28)^2{0.375(1-0.375)}}{(0.25)^2} = 79\). Thus, the investigator should enroll \(n_1 = 79\) patients into treatment and \(n_2 = 79\) into placebo for a total of 158 patients.
With an unequal allocation ratio of \(AR = 3, n_1 = 168\) and \(n_2 = 56\). Again, notice that the allocation ratio of AR = 3 yields a total sample size larger than that for the allocation ratio of AR = 1 (224 vs. 158).
This is a program that illustrates the use of PROC POWER to calculate sample size when comparing two binomial proportions.
***********************************************************************
* This is a program that illustrates the use of PROC POWER to *
* calculate sample size when comparing two binomial proportions. *
***********************************************************************;
proc power;
twosamplefreq groupweights=(1 1) groupps=(0.25 0.50) alpha=0.05 power=0.9
test=Fisher sides=2 ntotal=.;
plot min=0.1 max=0.9;
title "Sample Size Calculation for Comparing Two Binomial Proportions (1:1 Allocation)";
run;
proc power;
twosamplefreq groupweights=(1 3) groupps=(0.25 0.50) alpha=0.05 power=0.9
test=Fisher sides=2 ntotal=.;
plot min=0.1 max=0.9;
title "Sample Size Calculation for Comparing Two Binomial Proportions (3:1 Allocation)";
run;
SAS PROC POWER for Fisher’s exact test yields \(n_1 = 85\) and \(n_2 = 85\) for \(AR = 1\), and \(n_1 = 171\) and \(n_2 = 57\) for \(AR = 3\).
Try it!
The answer is a total of 752 subjects.
Here is the output you should have obtained from SAS ...
|
The POWER Procedure |
|
|---|---|
| Fixed Scenario Elements | |
| Distribution | Exact conditional |
| Method | Walter's normal approximation |
| Number of Sides | 2 |
| Alpha | 0.05 |
| Group 1 Proportion | 0.3 |
| Group 2 Proportion | 0.4 |
| Group 1 Weight | 1 |
| Group 2 Weight | 1 |
| Nominal Power | 0.8 |
| Computed N Total | |
|---|---|
| Actual Power | N Total |
| 0.801 | 752 |
6a.8 - Comparing Treatment Groups Using Hazard Ratios
6a.8 - Comparing Treatment Groups Using Hazard RatiosFor many clinical trials, the response is time to an event. The methods of analysis for this type of variable are generally referred to as survival analysis methods. The basic approach is to compare survival curves.
With an event time endpoint, it is mathematically convenient to compare treatment groups (and curves) with respect to the hazard ratio. The survival function for a treatment group is characterized by \(\lambda\), the hazard rate. At time t, \(\lambda(t)\) for a treatment group, is defined as the instantaneous risk of the event (or failure) occurring at time t. In other words, given that a subject has survived the event up to time t, the hazard at time t is the probability of the event occurring within the next instant. You can think of the hazard as the slope of the survival curve.
The hazard ratio is defined as the ratio of two hazard functions, \(\lambda_1(t)\) and \(\lambda_2(t)\), corresponding to two treatment groups. Typically, we assume proportional hazards, i.e., \(\Lambda= \dfrac{\lambda_1(t)}{\lambda_2(t)}\) is a constant function independent of time. The graphs on the next two slides illustrate the concept of proportional hazards.
\(\lambda_1(t)/\lambda_2(t)\) is constant, regardless of time
A hazard function may be constant, increasing, or decreasing over time, or even be a more complex function of time. In trials in which survival time is the outcome, an increasing hazard function indicates that the instantaneous risk of death increases throughout the trial.
\(\lambda_1(t)/\lambda_2(t)\) is a function of time
An example where the hazard function might be decreasing involves the disease ARDS (adult respiratory distress syndrome), whereby the risk of death is highest during the early stage of the disease.
A sample size formula for comparing the hazards of two groups via the logrank test (discussed later in the course) is expressed in terms of the total number of events, E, that need to occur. For a two-sided, α-level significance test with \(100 \left(1 - \beta \right)\%\) statistical power, hazard ratio Λ, and allocation ratio AR,
\( E=\left( \dfrac{(AR+1)^2}{AR}\right) \dfrac{\left( z_{1-\alpha/2} + z_{1-\beta} \right)^2}{ \left(log_e(\Lambda) \right)^2} \)
Since we do not expect all persons in the trial to experience an event, the sample size must be larger than the required number of events.
Suppose that \(p_1\) and \(p_2\) represent the anticipated event rates in the two treatment groups. Then the sample sizes can be determined from \(n_2 = \dfrac{E}{(AR \times p_1 + p_2)}\) and \(n_1 = AR \times n_2\)
If a hazard function is assumed to be constant during the follow-up period [0, T], then it can be expressed as \(\lambda(t) = \lambda = \dfrac{-log_e(1 - p)}{T}\). In such a situation, the hazard ratio for comparing two groups is \(\Lambda = \dfrac{log_e(1 - p_1)}{log_e(1 - p_2)}\).
A constant hazard rate, \(\lambda(t) = \lambda\) for all time points t, corresponds to an exponential survival curve, i.e., survival at time \(t = exp(-\lambda t)\).
Survival curves plot the probability of the event occurring to a subject over time.
SAS® Example
Using PROC POWER to calculate sample size when comparing two hazard functions
An investigator wants to compare an experimental therapy to placebo when the response is time to infection via a two-sided, 0.05-significance level test with 90% statistical power and equal allocation. He plans to follow each patient for one year and he expects that 40% of the placebo group will experience infection and he considers a 20% rate in the therapy group as clinically relevant.
If he assumes constant hazard functions, then
\(\Lambda= \dfrac{log_e(0.6)}{log_e(0.8)} = 2.29\)
Then the number of required events is
\(E = \dfrac{(4)(1.96 + 1.28)^2}{{log_e(2.29)}^2} = 62\)
and the sample sizes are
\(n_2 = \dfrac{E}{(AR \times p_1 + p_2)} = \dfrac{62}{(0.4 + 0.2)} = 104\) and \(n_1 = 104\)
SAS Example - This is a program that illustrates the use of PROC POWER to calculate sample size when comparing two hazard functions.
***********************************************************************
* This is a program that illustrates the use of PROC POWER to *
* calculate sample size when comparing two hazard functions. *
***********************************************************************;
proc power;
twosamplesurvival groupweights=(1 1) alpha=0.05 power=0.9 sides=2
test=logrank curve("Placebo")=(1.01):(0.6) curve("Therapy")=(1.01):(0.8)
groupsurvival="Placebo"|"Therapy" accrualtime=0.01 followuptime=1 ntotal=.;
plot min=0.1 max=0.9;
title "Sample Size Calculation for Comparing Two Hazard Functions (1:1 Allocation)";
run;
proc power;
twosamplesurvival groupweights=(1 3) alpha=0.05 power=0.9 sides=2
test=logrank curve("Placebo")=(1.01):(0.6) curve("Therapy")=(1.01):(0.8)
groupsurvival="Placebo"|"Therapy" accrualtime=0.01 followuptime=1 ntotal=.;
plot min=0.1 max=0.9;
title "Sample Size Calculation for Comparing Two Hazard Functions (3:1 Allocation)";
run;
Additional comments on this program: Note the curve statements indicate points on the survival curves. In this example, at the end of study, at time 1.01 (followup plus accrual in SAS), the proportion in the placebo group without an event is 0.6 and the proportion remaining the therapy group is 0.8.
SAS PROC POWER for the logrank test requires information on the accrual time and the follow-up time. It assumes that if the accrual (recruitment) period is of duration \(T_1\) and the follow-up time is of duration \(T_2\), then the total study time is of duration \(T_1 + T_2\). It assumes, however, if a patient is recruited at time \(\dfrac{T_1}{2}\), then the follow-up period for that patient is \(\dfrac{T_1}{2 + T_2}\) instead of \(T_2\). This assumption may be reasonable for observational studies, but not for clinical trials in which follow-up on each patient is terminated when the patient reaches time \(T_2\). Therefore, for a clinical trial situation, set accrual time in SAS PROC POWER equal to a very small positive number. For the given example, SAS PROC POWER yields \(n_1 = 109\) and \(n_2 = 109\).
6a.9 - Expanded Safety Studies
6a.9 - Expanded Safety StudiesExpanded Safety (ES) trials are phase IV trials designed to estimate the frequency of uncommon adverse events that may have been undetected in earlier studies. These studies may be nonrandomized.
Typically, we assume that the study population is large, the probability of an adverse event is small (because it did not crop up in prior trials), and all participants in the cohort of size m are followed for approximately the same length of time. Under these assumptions, we can model the probability of exactly d events occurring based on a Poisson probability function, i.e.,
\( Pr \left[ D = d \right] = ( \xi m)^d exp(- \xi m)/d! \)
where \( \xi \) is the adverse event rate.
The cohort should be large enough to have a high probability of observing at least one event when the event rate is \( \xi \). Thus, we want
\( \beta = Pr \left[D \ge 1 \right] = 1 - Pr \left[ D = 0 \right] = 1 - exp(-\xi m) \)
to be relatively large. With respect to the cohort size, this means that m should be selected such that
\( m = -log_e(1 - \beta)/ \xi \)
Example
Suppose a pharmaceutical company is planning an ES trial for a new anti-arrhythmia drug. The company wants to determine the cohort size for following patients on the drug for a period of two years in terms of myocardial infarction. They want to have a 0.99 probability \(\left(\beta = 0.99 \right)\) for detecting a myocardial infarction rate of one per thousand (\( \xi \) = 0.001).
m= -ln(0.01)/0.001
This yields a cohort size of m = 4,605.1. Rounded up, 4606.
(note the \(\beta\) value in this problem is a probability, not quite the same as \(\beta\) that we use in calculating power)
6a.10 - Adjustment Factors for Sample Size Calculations
6a.10 - Adjustment Factors for Sample Size CalculationsWhen calculating a sample size, we may need to adjust our calculations due to multiple primary comparisons or for nonadherence to therapy or to consider the anticipated dropout rate.
- If there is more than one primary outcome variable (for example, co-primary outcomes) or more than one primary comparison (for example, 3 treatment groups), then the significance level should be adjusted to account for the multiple comparisons in order not to inflate the overall false-positive rate.
For example, suppose a clinical trial will involve two treatment groups and a placebo group. The investigator may decide that there are two primary comparisons of interest, namely, each treatment group compared to placebo. The simplest adjustment to the significance level for each test is the Bonferroni correction, which uses \(\dfrac{\alpha}{2}\) instead of \(\alpha\).
In general, if there are K comparisons of primary interest, then the Bonferroni correction is to use a significance level of \(\dfrac{\alpha}{K}\) for each of the K comparisons. The Bonferroni correction is not the most powerful or most sophisticated multiple comparison adjustment, but it is a conservative approach and easy to apply.
In the case of multiple primary endpoints, an adjustment to the significance level may not be necessary, depending on how the investigator plans to interpret the results. For example, suppose there are two primary outcome variables. If the investigator plans to claim “success of the trial” if either endpoint yields a statistically significant treatment effect, then an adjustment to the significance level is warranted. If the investigator plans to claim “success of the trial” only if both endpoints yield statistically significant treatment effects, then an adjustment to the significance level is not necessary. Thus, an adjustment to the significance level in the presence of multiple primary endpoints depends on whether it is an “or” or an “and” situation.
(A composite outcome, such as "time to stroke, MI or major cardiovascular event", is different from a co-primary outcome. In this situation, when the composite results in one statistical analysis, there is no need for adjustment.)
- Another consideration is nonadhereance to the protocol (noncompliance). All participants randomized to therapy are expected to be included in the primary statistical analysis, an intention-to-treat analysis. Intention-to-treat analysis will compare the treatments using all data from subjects in the group to which they were originally assigned, regardless of whether or not they followed the protocol, stayed on therapy,etc. Some participants will choose to withdraw from a trial before it is complete. Every effort will be made to continue obtaining data from all randomized subjects; for those who withdraw from the study completely and do not provide data, an imputation procedure may be required to represent their missing data in subsequent data analyses. Some participants assigned to active therapy discontinue therapy but continue to provide data (therapeutic drop-outs). Some on a placebo or control add an active therapy (drop-ins) and continue to be observed. The nonadherence (noncompliance) can lead to a dilution of the treatment effect and lead to lower power for the study as well as biased estimates of treatment effects.
Thus, a further adjustment to the sample size estimate may be made based on the anticipated drop-out and drop-in rates in each arm (See Wittes (2002). A similar formula is on p. 179 FFDRG.
\(N^∗= \dfrac{N}{((1- R_O - R_I))^2}\) where N is the sample size without regard to nonadherence and N* is the adjusted number for that treatment arm.
\(R_O\) and \(R_I\) represent the proportion of participants anticipated to discontinue test therapy and the proportion in the control who will add or change to a more effective therapy, respectively.
- In other situations, an adjustment may be made to increase the sample size to account for the anticipated number of subjects who will drop-out of the study altogether so that there is sufficient power with the remaining observations to detect a certain difference. This adjustment is made by dividing the calculated sample size N by (1-W) where W is the proportion expected to withdraw.
\(N^{**}=\dfrac{N}{(1-W)}\)
Let's work an example.
Example
Suppose a study has two treatment groups and will compare test therapy to placebo. With only one primary comparison, we do not need to adjust the significance level for multiple comparisons. Suppose that the sample size for a certain power, significance level and clinically important difference works to be 200 participants/group or 400 total.
-
We plan an intention-to-treat analysis as our primary analysis and our concern is dilution of the true treatment effect due to these deviations from the assigned therapy. To adjust for noncompliance/nonadherence, we must estimate the proportion from the placebo group who will begin an active therapy before the study is complete. Let's estimate these 'drop-ins' to be 0.20. In the test therapy group, we estimate 0.10 will discontinue active therapy.
To adjust for noncompliance, we calculate \(N^{*} = 200/((1-0.2-0.1)^{2})\) . N^{*} = 409/\text{ group}\) or 818 total. What an increase in sample size to maintain the power! (note whether I use n/group, 200/(0.49) or total n, 400/(0.49) I will get the same sample sizes. Just remember what your N represents. If there is any fraction at the end of sample size calculations, round UP to the next number divisible by the number of treatment groups.)
-
Suppose instead of dilution of treatment effect in an ITT analysis, our concern is the proportion of subjects who will leave the study without providing a key observation on the primary outcome. If we anticipate a 15% rate of discontinuing before this measurement, we may want to increase the sample size accordingly. 200/0.85= 236/group (rounded up).
These are relatively simple calculations to introduce the idea of adjusting for noncompliance, multiple comparisons or the withdrawal rate. More complicated processes can be modeled.
Finally, when estimating a sample size for a study, an iterative process may be followed (adapted from Wittes, 2002)
- Determine the null and alternative hypotheses as related to the primary outcome.
- What is the desired type I error rate and power? If more than one primary outcome or comparison, make required adjustments to Type 1 error.
- Determine the population that will be studied. What information is there about the variability of the primary outcome in this population? Would would constitute a clinically important difference?
- If the study is measuring time to failure, how long is the followup period? What assumptions should be made about recruitment?
- Consider ranges of rates or events, loss to follow-up, competing risks, and noncompliance.
- Calculate sample size over a range of reasonable assumptions.
- Select a sample size. Plot power curves as the parameters range over reasonable values.
- Iterate as needed.
Which of these adjustments (or others, such as modeling dropout rates that are not independent of outcome) is important for a particular study depends on the study objectives. Not only must we consider whether there is more than one primary outcome or multiple primary comparisions, we must also consider the nature of the trial. For example, if the study results are headed to a regulatory agency, using a primary intention-to-treat analysis, it is important to demonstrate an effect of a certain magnitude. Adjusting the sample size to account for non-adherence is sensible. On the other hand, in a comparative effectiveness study, the objective may be to estimate the difference in effect when the intervention is prescribed vs the control, regardless of adherence. In this situation, the dilution of effect due to nonadherence may be of little concern.
As we noted beginning this lesson, sample size calculations are estimates! When stating a required sample size, always state any assumptions that have been made in the calculations.
6a.11 - Summary
6a.11 - SummaryIn this lesson, among other things, we learned to:
- Identify studies for which sample size is an important issue
- Estimate the sample size required for a confidence interval for p for given \(\delta\) and \(\alpha\), using normal approximation and Fisher's exact methods
- Estimate the sample size required for a confidence interval for μ for given \(\delta\) and \(\alpha\), using normal approximation when the sample size is relatively large
- Estimate the sample size required for a test of \(H_0 \colon \mu_1 = \mu_2\) to have \((1 - \beta)\%\) power for given \(\delta\) and \(\alpha\), using normal approximation, with equal or unequal allocation.
- Estimate the sample size required for a test of \(H_0 \colon p_1 = p_2\) for given \(\delta\) and \(\alpha\) and \(\beta\), using normal approximation and Fisher’s exact methods
- Use a SAS program to estimate the number of events required for a logrank comparison of two hazard functions to have \((1 - \beta)\%\) power with given \(\alpha\)
- Use Poisson probability methods to determine the cohort size required to have a certain probability of detecting a rare event that occurs at a \(\text{rate} = \xi\).
- Adjust sample size requirements to account for multiple comparisons and the anticipated noncompliance rates.