8.1.1 - Confidence Intervals
8.1.1 - Confidence IntervalsOn the following pages you will see how a confidence interval for a population proportion can be constructed by hand using the normal approximation method. Using Minitab, you will learn how to construct a confidence interval for a proportion using the normal approximation method or the exact method. When given the option, it is recommended that you use Minitab as opposed to performing calculations by hand.
8.1.1.1 - Normal Approximation Formulas
8.1.1.1 - Normal Approximation FormulasFor the following procedures, the assumption is that both \(np \geq 10\) and \(n(1-p) \geq 10\). When we're constructing confidence intervals \(p\) is typically unknown, in which case we use \(\widehat{p}\) as an estimate of \(p\).
Note that \(n \widehat p\) is the number of successes in the sample and \(n(1- \widehat p)\) is the number of failures in the sample.
This means that our sample needs to have at least 10 "successes" and at least 10 "failures" in order to construct a confidence interval using the normal approximation method.
Below is the general form of a confidence interval.
- General Form of Confidence Interval
- \(sample\ statistic\pm\underbrace{(multiplier)\ (standard\ error)}_{\textbf{margin of error}}\)
The sample statistic here is the sample proportion, \(\widehat p\). When using the normal approximation method the multiplier is taken from the standard normal distribution (i.e., z distribution). And, the standard error is computed using \(\widehat p\) as an estimate of \(p\): \(\sqrt{\frac{\hat{p} (1-\hat{p})}{n}}\). This leaves us with the following formula to construct a confidence interval for a population proportion:
- Confidence Interval of \(p\): Normal Approximation Method
- \(\underbrace{\widehat{p}}_{\text{sample statistic}} \pm \overbrace{z^{*}}^{\text{multiplier}} \underbrace{\left (\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\right)}_{\text{standard error}} \)
Finding the z* Multiplier
The value of the \(z^*\) multiplier depends on the level of confidence. The multiplier for the confidence interval for a population proportion can be found using the standard normal distribution [i.e., z distribution, N(0,1)]. The most commonly used level of confidence is 95%. As shown on the probability distribution plot below, the multiplier associated with a 95% confidence interval is 1.960, often rounded to 2 (recall the Empirical Rule and 95% Rule).
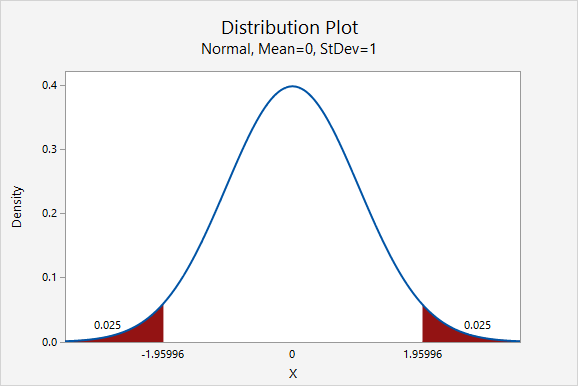
Below is a table of frequently used \(z^*\) multipliers.
| Confidence Level | \(z^*\) Multiplier |
|---|---|
| 90% | 1.645 |
| 95% | 1.960, often rounded to 2 |
| 98% | 2.327 |
| 99% | 2.576 |
The value of the multiplier increases as the confidence level increases. This leads to wider intervals for higher confidence levels. We are more confident of catching the population value when we use a wider interval.
8.1.1.1.1 - Video Example: PA Residency
8.1.1.1.1 - Video Example: PA Residency8.1.1.1.2 - Video Example: Dog Ownership
8.1.1.1.2 - Video Example: Dog OwnershipIn Spring 2016, a sample of 522 World Campus students were surveyed and asked if they own a dog. Of the 522 students in the sample, 273 said that they did have a dog. Construct a 95% confidence interval for the proportion of all World Campus students who have a dog.
8.1.1.1.3 - Video Example: Books
8.1.1.1.3 - Video Example: Books8.1.1.1.4 - Example: Retirement
8.1.1.1.4 - Example: RetirementIn a representative sample of 1168 American adults, 747 said they were not financially prepared for retirement. Let's construct a 95% confidence interval to estimate the proportion of all American adults who are not financially prepared for retirement.
First, we need to check our assumptions that both \(n\widehat p \geq 10\) and \(n(1-\widehat p) \geq 10\).
\(\widehat{p}=\frac{747}{1168}=0.640\)
\(np=1168 (0.640) = 747\) and \(n(1-p)=1168(1-0.640)=421\)
Both are greater than 10, so this assumption has been met. This means we can use the normal approximation method to construct this confidence interval.
Next, we can compute the standard error.
\(SE=\sqrt{\frac{\hat{p} (1-\hat{p})}{n}}=\sqrt{\frac{0.640 (1-0.640)}{1168}}=0.014\)
The \(z^*\) multiplier for a 95% confidence interval is 1.960
The formula for a confidence interval for a proportion is \(\widehat{p}\pm z^* (SE)\)
\(0.640\pm 1.960(0.014)=0.640\pm0.028=[0.612, \;0.668]\)
We are 95% confident that between 61.2% and 66.8% of all American adults are not financially prepared for retirement.
Let’s think about how our interval will change. The 99% confidence interval will be wider than the 95% confidence interval. In order to increase our level of confidence, we will need to expand the interval.
In terms of computing the 99% confidence interval, we will use the same point estimate \(\widehat{p}\) and the same standard error. Only the multiplier will change. From the plot below, we see that the \(z^*\) multiplier for a 99% confidence interval is 2.576.
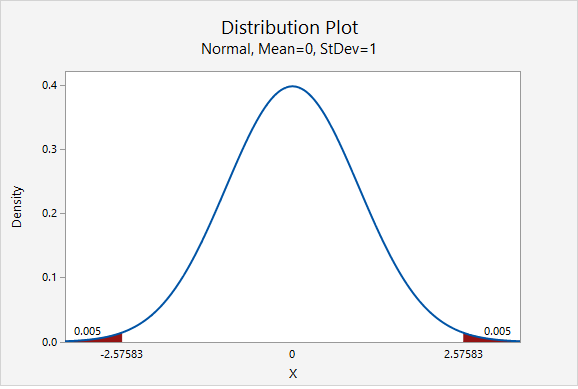
\(99\%\;C.I.:\;0.640\pm 2.576 (0.014)=0.0640\pm 0.036=[0.604, \; 0.676]\)
We are 99% confidence that between 60.4% and 67.6% of all American adults are not financially prepared for retirement.
8.1.1.2 - Minitab: Confidence Interval for a Proportion
8.1.1.2 - Minitab: Confidence Interval for a ProportionBefore we can construct a confidence interval for a proportion we must first determine if we should use the exact method or the normal approximation method. Recall that if \(np \geq 10\) and \(n(1-p) \geq 10\) then the sampling distribution can be approximated by a normal distribution. Since we don't have the population proportion (\(p\)), we using \(\widehat p\) as an estimate. Note that \(n\widehat p\) is the number of successes in the sample and \(n(1-\widehat p)\) is the number of failures in the sample.
If this assumption has not been met, then the sampling distribution is constructed using a binomial distribution which Minitab refers to as the "exact method."
To check this assumption we can construct a frequency table. You first learned how to construct a frequency table in Lesson 2.1.1.2.1 of these online notes. Here is another example:
Minitab® – Frequency Tables
To create a frequency table of dog ownership in Minitab:
- Open the data set:
- From the toolbar in Minitab, select Stat > Tables > Tally Individual Variables
- Double click the variable Dog in the box on the left to insert the variable into the Variable box
- Under Display, choose Counts
- Click OK
This should result in the following frequency table:
| Dog | Count |
|---|---|
| No | 252 |
| Yes | 272 |
| N= | 524 |
| *= | 1 |
From the frequency table above we can see that there were at least 10 "successes" and at least 10 "failures" in the sample. In this example a success is defined as answering "yes" to the question "do you own a dog?" A failure is defined as answering "no." Because both \(n \widehat p \geq 10\) and \(n(1- \widehat p) \geq 10\), the normal approximation method may be used. In Minitab, the exact method is the default method. If there are at least 10 successes and at least 10 failures, then you need to change the method to the normal approximation method.
Minitab® – Confidence Interval for a Proportion (Normal Approximation)
To create a 95% confidence interval of dog ownership using the normal approximation method in Minitab:
- Open the data set: fall2016stdata.mpx
- In Minitab, select Stat > Basic Statistics > 1-Proportion
- In this case we have our data in the Minitab worksheet so we will use the default One or more samples each in a column.
- Double click the variable Dog in the box on the left to insert the variable into the box.
- Select Options
- The default Confidence level is 95
- Change the Method to Normal approximation because the assumption of \(n \widehat p \geq 10\) and \(n(1- \widehat p) \geq 10\) has been met
- Click OK
This should result in the following output:
Method
Event: Dog = Yes
p: proportion where Dog = Yes
Normal approximation is used for this analysis.
| N | Event | Sample p | 95% CI for p |
|---|---|---|---|
| 524 | 272 | 0.519084 | (0.476304, 0.561863) |
What if the assumption is not met?
If the number of successes or the number of failures in the sample is less than 10, then the exact method should be used instead of the normal approximation method. In Minitab, this means that in step 8 above the default setting of Exact method should not be changed.
If you do not have a Minitab worksheet filled with data concerning individuals, but instead have summarized data (e.g., the number of successes and the number of failures), you would not load the data set, but in step 3 you would select Summarized data. For Number of events, enter the number of successes (i.e., \(n \widehat p\)) and for Number of trials enter the total sample size (i.e., \(n\)).
8.1.1.2.1 - Example with Summarized Data
8.1.1.2.1 - Example with Summarized DataExample: Lactose Intolerance
In a sample of 100 African American adults, 70 were identified as having some level of lactose intolerance. Compute a 95% confidence interval to estimate the proportion of all African American adults who have some level of lactose intolerance.
To create a 95% confidence interval of dog ownership using the normal approximation method in Minitab:
-
- In this case we have summarized data so select Summarized data in the dropdown.
- For number of events, add 70 and for number of trials add 100.
- Select Options
- The default Confidence level is 95.
- Change the Method to Normal approximation because the assumption of \(n \widehat p \geq 10\) and \(n(1- \widehat p) \geq 10\) has been met
- Click OK and OK.
This should result in the following output:
Method
p: event proportion
Normal approximation is used for this analysis.
| N | Event | Sample p | 95% CI for p |
|---|---|---|---|
| 100 | 70 | 0.700000 | (0.610183, 0.789817) |
8.1.1.2.2 - Example with Summarized Data
8.1.1.2.2 - Example with Summarized DataExample: Dieting
At the beginning of the Fall 2016 semester a representative sample of World Campus STAT 200 students was surveyed. The students were asked if they were currently dieting to lose weight. In the sample of 524 students, 184 said that they were dieting to lose weight. Construct a 95% confidence interval for the proportion of all World Campus STAT 200 students who are dieting to lose weight.
-
- In this case we have summarized data so select Summarized data in the dropdown.
- For number of events, add 184 and for number of trials add 524.
- Select Options
- The default Confidence level is 95.
- Change the Method to Normal approximation because the assumption of \(n \widehat p \geq 10\) and \(n(1- \widehat p) \geq 10\) has been met
- Click OK and OK.
This should result in the following output:
Method
p: event proportion
Normal approximation is used for this analysis.
| N | Event | Sample p | 95% CI for p |
|---|---|---|---|
| 524 | 184 | 0.351145 | (0.310276, 0.392015) |
8.1.1.3 - Computing Necessary Sample Size
8.1.1.3 - Computing Necessary Sample SizeWhen we begin a study to estimate a population parameter we typically have an idea as how confident we want to be in our results and within what degree of accuracy. This means we get started with a set level of confidence and margin of error. We can use these pieces to determine a minimum sample size needed to produce these results by using algebra to solve for \(n\):
- Finding Sample Size for Estimating a Population Proportion
- \(n=\left ( \dfrac{z^*}{M} \right )^2 \tilde{p}(1-\tilde{p})\)
-
\(M\) is the margin of error
\(\tilde p\) is an estimated value of the proportion
If we have no preconceived idea of the value of the population proportion, then we use \(\tilde{p}=0.50\) because it is most conservative and it will give use the largest sample size calculation.
Example: No Estimate
We want to construct a 95% confidence interval for \(p\) with a margin of error equal to 4%.
Because there is no estimate of the proportion given, we use \(\tilde{p}=0.50\) for a conservative estimate.
For a 95% confidence interval, \(z^*=1.960\)
\(n=\left ( \dfrac{1.960}{0.04} \right )^2 (0.5)(1-0.5)=600.25\)
This is the minimum sample size, therefore we should round up to 601. In order to construct a 95% confidence interval with a margin of error of 4%, we should obtain a sample of at least \(n=601\).
Example: Estimate Known
We want to construct a 95% confidence interval for \(p\) with a margin of error equal to 4%. What if we knew that the population proportion was around 0.25?
The \(z^*\) multiplier for a 95% confidence interval is 1.960. Now, we have an estimate to include in the formula:
\(n=\left ( \dfrac{1.960}{0.04} \right )^2 (0.25)(1-0.25)=450.188\)
Again, we should round up to 451. In order to construct a 95% confidence interval with a margin of error of 4%, given \(\tilde{p}=.25\), we should obtain a sample of at least \(n=451\).
Note that when we changed \(\tilde{p}\) in the formula from .50 to .25, the necessary sample size decreased from \(n=601\) to \(n=451\).