11.1 - Reviews
11.1 - ReviewsIn this lesson you may need to use Minitab to construct frequency tables or two-way contingency tables. We'll start by reviewing these procedures. You will need to construct probability distribution plots for chi-square distributions. In earlier lessons we constructed probability distribution plots for z, t, and F distributions; the procedure is similar for a chi-square distribution. We will also review conditional probabilities and the term independence in this section.
11.1.1 - Frequency Table
11.1.1 - Frequency TableThe following example was first presented in Lesson 2.1.1.2.1.
It uses following data set (from College Board):
Minitab® – Frequency Tables
To create a frequency table in Minitab:
- Open the Minitab file: sat_data.mpx
- Select Stat > Tables > Tally Individual Variables
- Double click the variable Region in the box on the left to insert the variable into the Variable box
- Under Statistics, check Counts and Percents
- Click OK
This should result in the following frequency table:
Tally
| Region | Count | Percent |
|---|---|---|
| ENC | 5 | 9.80 |
| ESC | 4 | 7.84 |
| MA | 3 | 5.88 |
| MTN | 8 | 15.69 |
| NE | 6 | 11.76 |
| PAC | 5 | 9.80 |
| SA | 9 | 17.65 |
| WNC | 7 | 13.73 |
| WSC | 4 | 7.84 |
| N= | 51 |
11.1.2 - Two-Way Contingency Table
11.1.2 - Two-Way Contingency TableRecall from Lesson 2.1.2 that a two-way contingency table is a display of counts for two categorical variables in which the rows represented one variable and the columns represent a second variable. The starting point for analyzing the relationship between two categorical variables is to create a two-way contingency table. When one variable is obviously the explanatory variable, the convention is to use the explanatory variable to define the rows and the response variable to define the columns; this is not a hard and fast rule though.
Minitab® – Constructing a Two-Way Contingency Table
- Open the data set: class_survey.mpx
- Select Stat > Tables > Cross Tabulation and Chi-square
- Select Raw data (categorical variable) from the drop down menu
- Double click the variable Smoke Cigarettes in the box on the left to insert the variable into the Rows box
- Double click the variable Biological Sex in the box on the left to insert the variable into the Columns box
- Click OK
This should result in the two-way table below:
Rows: Smokes Cigaretes | Columns: Biological Sex
| Female | Male | All | |
|---|---|---|---|
| No | 120 | 89 | 209 |
| Yes | 7 | 10 | 17 |
| All | 127 | 99 | 226 |
| Cell Contents: Count | |||
11.1.3 - Probability Distribution Plots
11.1.3 - Probability Distribution PlotsIn previous lessons you have constructed probabilities distribution plots for normal distributions, binomial distributions, and \(t\) distributions. This week you will use the same procedure to construct a probability distribution plot for the chi-square distribution.
Minitab® – Constructing a Probability Distribution Plot
Chi-square tests of independence are always right-tailed tests. Let's find the area of a chi-square distribution with 1 degree of freedom to the right of \(\chi^2 = 1.75\). In other words, we're looking up the \(p\) value associated with a chi-square test statistic of 1.75.
- In Minitab, select Graph > Probability Distribution Plot > View Probability
- Choose Chi-Square for the Distribution
- For Distribution select Chi-Square
- For Degrees of freedom enter 1
- Select A specified X value
- Select Right tail
- For X value enter 1.75
- Select OK and OK
This should result in the following output:
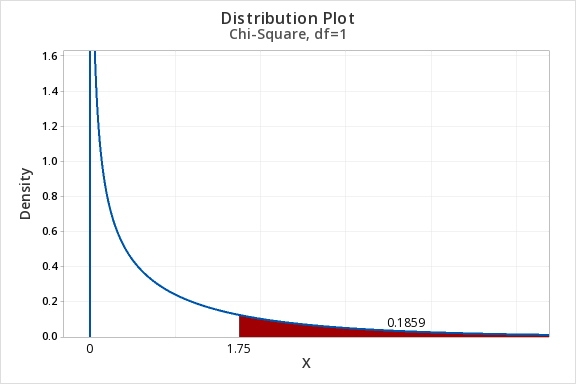
Example: Area to the Right of Chi-Sq = 6.25, df=3
Construct a chi-square distribution with 3 degrees of freedom to find the area to the right of a chi-square value of 6.25.
- In Minitab, select Graph > Probability Distribution Plot > View Probability
- Choose Chi-Square for the Distribution
- For Distribution select Chi-Square
- For Degrees of freedom enter 3
- Select A specified X value
- Select Right tail
- For X value enter 6.25
- Select OK and OK
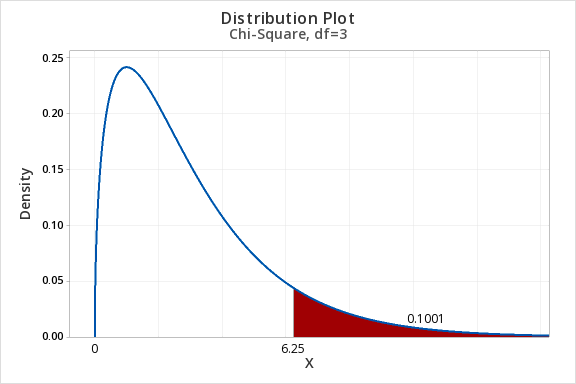
The area to the right of 6.25 in the chi-square distribution with 3 degrees of freedom is 0.1001.
11.1.4 - Conditional Probabilities and Independence
11.1.4 - Conditional Probabilities and IndependenceIn Lesson 2 you were introduced to conditional probabilities and independent events. These definitions are reviewed below along with some examples.
Recall that if events A and B are independent then \(P(A) = P(A \mid B)\). In other words, whether or not event B occurs does not change the probability of event A occurring.
- Conditional Probability
-
The probability of one event occurring given that it is known that a second event has occurred. This is communicated using the symbol \(\mid\) which is read as "given."
For example, \(P(A\mid B)\) is read as "Probability of A given B."
- Independent Events
- Unrelated events. The outcome of one event does not impact the outcome of the other event.
Example: Queens & Hearts
If a card is randomly drawn from a standard 52-card deck, the probability of the card being a queen is independent from the probability of the card being a heart. If I tell you that a randomly selected card is a queen, that does not change the likelihood of it being a heart, diamond, club, or spade.
Using a conditional probability to prove this:
\(P(Queen) = \dfrac{4}{52}=0.077\)
\(P(Queen \mid Heart) = \dfrac {1}{13} = 0.077\)
Example: Gender and Pass Rate
Data concerning two categorical variables can be displayed in a contingency table.
| Pass | Did Not Pass | Total | |
| Men | 6 | 9 | 15 |
| Women | 10 | 15 | 25 |
| Total | 16 | 24 | 40 |
If gender and passing are independent, then the probability of passing will not change if a case's gender is known. This could be written as \(P(Pass) = P(Pass \mid Man)\).
\(P(Pass) = \dfrac{16}{40} = 0.4\)
\(P(Pass \mid Man) = \dfrac{6}{15}=0.4\)
In this sample, gender and passing are independent.