12.3 - Highly Correlated Predictors
12.3 - Highly Correlated PredictorsOkay, so we've learned about all the good things that can happen when predictors are perfectly or nearly perfectly uncorrelated. Now, let's discover the bad things that can happen when predictors are highly correlated.
What happens if the predictor variables are highly correlated?
Let's return to the Blood Pressure data set. This time, let's focus, however, on the relationships among the response y = BP and the predictors \(x_2\) = Weight and \(x_3\) = BSA:
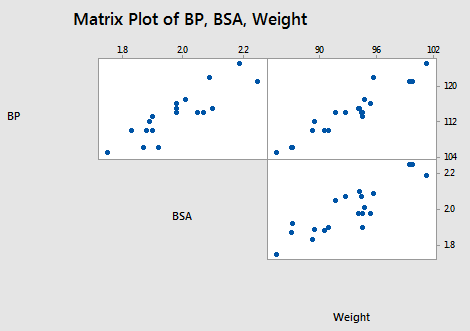
As the matrix plot and the following correlation matrix suggest:
Correlation: BP, Age, Weight, BSA, Dur, Pulse, Stress
| BP | Age | Weight | BSA | Dur | Pulse | |
|---|---|---|---|---|---|---|
| Age | 0.659 | |||||
| Weight | 0.950 | 0.407 | ||||
| BSA | 0.866 | 0.378 | 0.875 | |||
| Dur | 0.293 | 0.344 | 0.201 | 0.131 | ||
| Pulse | 0.721 | 0.619 | 0.659 | 0.465 | 0.402 | |
| Stress | 0.164 | 0.368 | 0.034 | 0.018 | 0.312 | 0.506 |
there appears to be not only a strong relationship between y = BP and \(x_2\) = Weight (r = 0.950) and a strong relationship between y = BP and the predictor \(x_3\) = BSA (r = 0.866), but also a strong relationship between the two predictors \(x_2\) = Weight and \(x_3\) = BSA (r = 0.875). Incidentally, it shouldn't be too surprising that a person's weight and body surface area are highly correlated.
What impact does the strong correlation between the two predictors have on the regression analysis and the subsequent conclusions we can draw? Let's proceed as before by reviewing the output of a series of regression analyses and collecting various pieces of information along the way. When we're done, we'll review what we learned by collating the various items in a summary table.
The regression of the response y = BP on the predictor \(x_2\)= Weight:
Analysis of Variance
| Source | DF | Seq SS | Seq MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 1 | 505.472 | 505.472 | 166.86 | 0.000 |
| Weight | 1 | 505.472 | 505.472 | 166.86 | 0.000 |
| Error | 18 | 54.528 | 3.029 | ||
| Lack-of-Fit | 17 | 54.028 | 3.178 | 6.36 | 0.303 |
| Pure Error | 1 | 0.500 | 0.500 | ||
| Total | 19 | 560.00 |
Modal Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 1.74050 | 90.23% | 89.72% | 88.53% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 2.21 | 8.66 | 0.25 | 0.802 | |
| Weight | 1.2009 | 0.0930 | 12.92 | 0.000 | 1.00 |
Regression Equation
\(\widehat{BP} = 2.21 + 1.2009 Weight\)
yields the estimated coefficient \(b_2\) = 1.2009, the standard error se(\(b_2\)) = 0.0930, and the regression sum of squares SSR(\(x_2\)) = 505.472.
The regression of the response y = BP on the predictor \(x_3\)= BSA:
Analysis of Variance
| Source | DF | Seq SS | Seq MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 1 | 419.858 | 419.858 | 53.93 | 0.000 |
| BSA | 1 | 419.858 | 419.858 | 53.93 | 0.000 |
| Error | 18 | 140.142 | 7.786 | ||
| Lack-of-Fit | 13 | 133.642 | 10.280 | 7.91 | 0.016 |
| Pure Error | 5 | 6.500 | 1.300 | ||
| Total | 19 | 560.00 |
Modal Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 2.79028 | 74.97% | 73.58% | 69.55% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 45.18 | 9.39 | 4.81 | 0.000 | |
| BSA | 34.44 | 4.69 | 7.34 | 0.000 | 1.00 |
Regression Equation
\(\widehat{BP} = 45.18 + 34.44 BSA\)
yields the estimated coefficient \(b_3\) = 34.44, the standard error se(\(b_3\)) = 4.69, and the regression sum of squares SSR(\(x_3\)) = 419.858.
The regression of the response y = BP on the predictors \(x_2\)= Weight and \(x_3 \)= BSA (in that order):
Analysis of Variance
| Source | DF | Seq SS | Seq MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 2 | 508.286 | 254.143 | 83.54 | 0.000 |
| Weight | 1 | 505.472 | 505.472 | 166.16 | 0.000 |
| BSA | 1 | 2.814 | 2.814 | 0.93 | 0.350 |
| Error | 17 | 51.714 | 3.042 | ||
| Total | 19 | 560.00 |
Modal Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 1.74413 | 90.77% | 89.68% | 87.78% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 5.65 | 9.39 | 0.60 | 0.555 | |
| Weight | 1.039 | 0.193 | 5.39 | 0.000 | 4.28 |
| BSA | 5.83 | 6.06 | 0.96 | 0.350 | 4.28 |
Regression Equation
\(\widehat{BP} = 5.65 + 1.039 Weight + 5.83 BSA\)
yields the estimated coefficients \(b_2\) = 1.039 and \(b_3\) = 5.83, the standard errors se(\(b_2\)) = 0.193 and se(\(b_3\)) = 6.06, and the sequential sum of squares SSR(\(x_3\)|\(x_2\)) = 2.814.
And finally, the regression of the response y = BP on the predictors \(x_3\)= BSA and \(x_2\)= Weight (in that order):
Analysis of Variance
| Source | DF | Seq SS | Seq MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 2 | 508.29 | 254.143 | 83.54 | 0.000 |
| BSA | 1 | 419.86 | 419.858 | 138.02 | 0.000 |
| Weight | 1 | 88.43 | 88.428 | 29.07 | 0.000 |
| Error | 17 | 51.71 | 3.042 | ||
| Total | 19 | 560.00 |
Modal Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 1.74413 | 90.77% | 89.68% | 87.78% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 5.65 | 9.39 | 0.60 | 0.555 | |
| BSA | 5.83 | 6.06 | 0.96 | 0.350 | 4.28 |
| Weight | 1.039 | 0.193 | 5.39 | 0.000 | 4.28 |
Regression Equation
\(\widehat{BP} = 5.65 + 5.83 BSA + 1.039 Weight\)
yields the estimated coefficients \(b_2\) = 1.039 and \(b_3\) = 5.83, the standard errors se(\(b_2\)) = 0.193 and se(\(b_3\)) = 6.06, and the sequential sum of squares SSR(\(x_2\)|\(x_3\)) = 88.43.
Compiling the results in a summary table, we obtain:
|
Model |
\(b_2\) | se(\(b_2\)) | \(b_3\) | se(\(b_3\)) | Seq SS |
|---|---|---|---|---|---|
| \(x_2\) only | 1.2009 | 0.0930 | --- | --- | SSR(\(x_2\)) 505.472 |
| \(x_3\) only | --- | --- | 34.44 | 4.69 | SSR(\(x_3\)) 419.858 |
| \(x_2\), \(x_3\) (in order) |
1.039 | 0.193 | 5.83 | 6.06 | SSR(\(x_3\)|\(x_2\)) 2.814 |
| \(x_3\), \(x_2\) (in order) |
1.039 | 0.193 | 5.83 | 6.06 | SSR(\(x_2\)|\(x_3\)) 88.43 |
Geez — things look a little different than before. It appears as if, when predictors are highly correlated, the answers you get depend on the predictors in the model. That's not good! Let's proceed through the table and in so doing carefully summarize the effects of multicollinearity on the regression analyses.
When predictor variables are correlated, the estimated regression coefficient of any one variable depends on which other predictor variables are included in the model.
Here's the relevant portion of the table:
|
Variables in model |
\(b_2\) | \(b_3\) |
|---|---|---|
| \(x_2\) | 1.20 | --- |
| \(x_3\) | --- | 34.4 |
| \(x_2\), \(x_3\) | 1.04 | 5.83 |
Note that, depending on which predictors we include in the model, we obtain wildly different estimates of the slope parameter for \(x_3\) = BSA!
- If \(x_3\) = BSA is the only predictor included in our model, we claim that for every additional one square meter increase in body surface area (BSA), blood pressure (BP) increases by 34.4 mm Hg.
- On the other hand, if \(x_2\) = Weight and \(x_3\) = BSA are both included in our model, we claim that for every additional one square meter increase in body surface area (BSA), holding weight constant, blood pressure (BP) increases by only 5.83 mm Hg.
This is a huge difference! Our hope would be, of course, that two regression analyses wouldn't lead us to such seemingly different scientific conclusions. The high correlation between the two predictors is what causes the large discrepancy. When interpreting \(b_3\) = 34.4 in the model that excludes \(x_2\) = Weight, keep in mind that when we increase \(x_3\) = BSA then \(x_2\) = Weight also increases and both factors are associated with increased blood pressure. However, when interpreting \(b_3\) = 5.83 in the model that includes \(x_2\) = Weight, we keep \(x_2\) = Weight fixed, so the resulting increase in blood pressure is much smaller.
The fantastic thing is that even predictors that are not included in the model, but are highly correlated with the predictors in our model, can have an impact! For example, consider a pharmaceutical company's regression of territory sales on territory population and per capita income. One would, of course, expect that as the population of the territory increases, so would the sales in the territory. But, contrary to this expectation, the pharmaceutical company's regression analysis deemed the estimated coefficient of territory population to be negative. That is, as the population of the territory increases, the territory sales were predicted to decrease. After further investigation, the pharmaceutical company determined that the larger the territory, the larger to the competitor's market penetration. That is, the competitor kept the sales down in territories with large populations.
In summary, the competitor's market penetration was not included in the original model. Yet, it was later deemed to be strongly positively correlated with territory population. Even though the competitor's market penetration was not included in the original model, its strong correlation with one of the predictors in the model, greatly affected the conclusions arising from the regression analysis.
The moral of the story is that if you get estimated coefficients that just don't make sense, there is probably a very good explanation. Rather than stopping your research and running off to report your unusual results, think long and hard about what might have caused the results. That is, think about the system you are studying and all of the extraneous variables that could influence the system.
When predictor variables are correlated, the precision of the estimated regression coefficients decreases as more predictor variables are added to the model.
Here's the relevant portion of the table:
|
Variables in model |
se(\(b_2\)) | se(\(b_3\)) |
|---|---|---|
| \(x_2\) | 0.093 | --- |
| \(x_3\) | --- | 4.69 |
| \(x_2\), \(x_3\) | 0.193 | 6.06 |
The standard error for the estimated slope \(b_2\) obtained from the model including both \(x_2\) = Weight and \(x_3\) = BSA is about double the standard error for the estimated slope \(b_2\) obtained from the model including only \(x_2\) = Weight. And, the standard error for the estimated slope \(b_3\) obtained from the model including both \(x_2\) = Weight and \(x_3\) = BSA is about 30% larger than the standard error for the estimated slope \(b_3\) obtained from the model including only \(x_3\) = BSA.
What is the major implication of these increased standard errors? Recall that the standard errors are used in the calculation of the confidence intervals for the slope parameters. That is, increased standard errors of the estimated slopes lead to wider confidence intervals and hence less precise estimates of the slope parameters.
Three plots to help clarify the second effect. Recall that the first Uncorrelated Predictors data set that we investigated in this lesson contained perfectly uncorrelated predictor variables (r = 0). Upon regressing the response y on the uncorrelated predictors \(x_1\) and \(x_2\), Minitab (or any other statistical software for that matter) will find the "best fitting" plane through the data points:
Click the Best Fitting Plane button to see the best-fitting plane for this particular set of responses. Now, here's where you have to turn on your imagination. The primary characteristic of the data — because the predictors are perfectly uncorrelated — is that the predictor values are spread out and anchored in each of the four corners, providing a solid base over which to draw the response plane. Now, even if the responses (y) varied somewhat from sample to sample, the plane couldn't change all that much because of the solid base. That is, the estimated coefficients, \(b_1\) and \(b_2\) couldn't change that much, and hence the standard errors of the estimated coefficients, se(\(b_1\)) and se(\(b_2\)) will necessarily be small.
Now, let's take a look at the second example (bloodpress.txt) that we investigated in this lesson, in which the predictors \(x_3\) = BSA and \(x_6\) = Stress were nearly perfectly uncorrelated (r = 0.018). Upon regressing the response y = BP on the nearly uncorrelated predictors \(x_3\) = BSA and \(x_6 \) = Stress, we will again find the "best fitting" plane through the data points. Move the slider at the bottom of the graph to see the plane of best fit.
Again, the primary characteristic of the data — because the predictors are nearly perfectly uncorrelated — is that the predictor values are spread out and just about anchored in each of the four corners, providing a solid base over which to draw the response plane. Again, even if the responses (y) varied somewhat from sample to sample, the plane couldn't change all that much because of the solid base. That is, the estimated coefficients, \(b_3\) and \(b_6\) couldn't change all that much. The standard errors of the estimated coefficients, se(\(b_3\)) and se(\(b_6\)), again will necessarily be small.
Now, let's see what happens when the predictors are highly correlated. Let's return to our most recent example (bloodpress.txt), in which the predictors \(x_2\) = Weight and \(x_3\) = BSA are very highly correlated (r = 0.875). Upon regressing the response y = BP on the predictors \(x_2\) = Weight and \(x_3\) = BSA, Minitab will again find the "best fitting" plane through the data points.
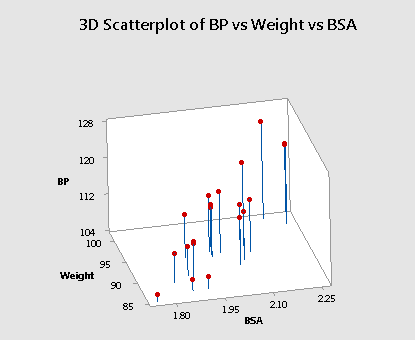
Do you see the difficulty in finding the best-fitting plane in this situation? The primary characteristic of the data — because the predictors are so highly correlated — is that the predictor values tend to fall in a straight line. That is, there are no anchors in two of the four corners. Therefore, the base over which the response plane is drawn is not very solid.
Let's put it this way — would you rather sit on a chair with four legs or one with just two legs? If the responses (y) varied somewhat from sample to sample, the position of the plane could change significantly. That is, the estimated coefficients, \(b_2\) and \(b_3\) could change substantially. The standard errors of the estimated coefficients, se(\(b_2\)) and se(\(b_3\)), will then be necessarily larger. Below is an animated view (no sound) of the problem that highly correlated predictors can cause with finding the best fitting plane.
When predictor variables are correlated, the marginal contribution of any one predictor variable in reducing the error sum of squares varies depending on which other variables are already in the model.
For example, regressing the response y = BP on the predictor \(x_2\) = Weight, we obtain SSR(\(x_2\)) = 505.472. But, regressing the response y = BP on the two predictors \(x_3\) = BSA and \(x_2\) = Weight (in that order), we obtain SSR(\(x_2\)|\(x_3\)) = 88.43. The first model suggests that weight reduces the error sum of squares substantially (by 505.472), but the second model suggests that weight doesn't reduce the error sum of squares all that much (by 88.43) once a person's body surface area is taken into account.
This should make intuitive sense. In essence, weight appears to explain some of the variations in blood pressure. However, because weight and body surface area are highly correlated, most of the variation in blood pressure explained by weight could just have easily been explained by body surface area. Therefore, once you take into account a person's body surface area, there's not much variation left in the blood pressure for weight to explain.
Incidentally, we see a similar phenomenon when we enter the predictors into the model in reverse order. That is, regressing the response y = BP on the predictor \(x_3\) = BSA, we obtain SSR(\(x_3\)) = 419.858. But, regressing the response y = BP on the two predictors \(x_2\) = Weight and \(x_3\) = BSA (in that order), we obtain SSR(\(x_3\)|\(x_2\)) = 2.814. The first model suggests that body surface area reduces the error sum of squares substantially (by 419.858), and the second model suggests that body surface area doesn't reduce the error sum of squares all that much (by only 2.814) once a person's weight is taken into account.
When predictor variables are correlated, hypothesis tests for \(\beta_k = 0\) may yield different conclusions depending on which predictor variables are in the model. (This effect is a direct consequence of the three previous effects.)
To illustrate this effect, let's once again quickly proceed through the output of a series of regression analyses, focusing primarily on the outcome of the t-tests for testing \(H_0 \colon \beta_{BSA} = 0 \) and \(H_0 \colon \beta_{Weight} = 0 \).
The regression of the response y = BP on the predictor \(x_3\)= BSA:
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 45.18 | 9.39 | 4.81 | 0.000 | |
| BSA | 34.44 | 4.69 | 7.34 | 0.000 | 1.00 |
Regression Equation
\(\widehat{BP} = 45.18 + 34.44 BSA\)
indicates that the P-value associated with the t-test for testing\(H_0 \colon \beta_{BSA} = 0 \) is 0.000... < 0.01. There is sufficient evidence at the 0.05 level to conclude that blood pressure is significantly related to body surface area.
The regression of the response y = BP on the predictor \(x_2\) = Weight:
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 2.21 | 8.66 | 0.25 | 0.802 | |
| Weight | 1.2009 | 0.0930 | 12.92 | 0.000 | 1.00 |
Regression Equation
\(\widehat{BP} = 2.21 + 1.2009 Weight\)
indicates that the P-value associated with the t-test for testing\(H_0 \colon \beta_{Weight} \) = 0 is 0.000... < 0.01. There is sufficient evidence at the 0.05 level to conclude that blood pressure is significantly related to weight.
And, the regression of the response y = BP on the predictors \(x_2\) = Weight and \(x_3\) = BSA:
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 5.65 | 9.39 | 0.60 | 0.555 | |
| Weight | 1.039 | 0.193 | 5.39 | 0.000 | 4.28 |
| BSA | 5.83 | 6.06 | 0.96 | 0.350 | 4.28 |
Regression Equation
\(\widehat{BP} = 112.72 + 0.0240 Stress\)
indicates that the P-value associated with the t-test for testing\(H_0 \colon \beta_{Weight} \) = 0 is 0.000... < 0.01. There is sufficient evidence at the 0.05 level to conclude that, after taking into account body surface area, blood pressure is significantly related to weight.
The regression also indicates that the P-value associated with the t-test for testing\(H_0 \colon \beta_{BSA} = 0 \) is 0.350. There is insufficient evidence at the 0.05 level to conclude that blood pressure is significantly related to body surface area after taking into account weight. This might sound contradictory to what we claimed earlier, namely that blood pressure is indeed significantly related to body surface area. Again, what is going on here, once you take into account a person's weight, body surface area doesn't explain much of the remaining variability in blood pressure readings.
High multicollinearity among predictor variables does not prevent good, precise predictions of the response within the scope of the model.
Well, okay, it's not an effect, and it's not bad news either! It is good news! If the primary purpose of your regression analysis is to estimate a mean response \(\mu_Y\) or to predict a new response y, you don't have to worry much about multicollinearity.
For example, suppose you are interested in predicting the blood pressure (y = BP) of an individual whose weight is 92 kg and whose body surface area is 2 square meters:
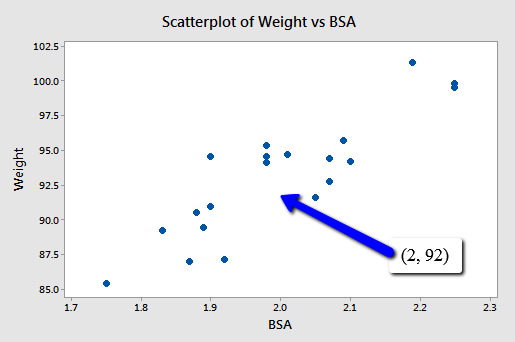
Because point (2, 92) falls within the scope of the model, you'll still get good, reliable predictions of the response y, regardless of the correlation that exists among the two predictors BSA and Weight. Geometrically, what is happening here is that the best-fitting plane through the responses may tilt from side to side from sample to sample (because of the correlation), but the center of the plane (in the scope of the model) won't change all that much.
The following output illustrates how the predictions don't change all that much from model to model:
| Weight | Fit | SE Fit | 95.0% CI | 95.0% PI |
|---|---|---|---|---|
| 92 | 112.7 | 0.402 | (111.85, 113.54) | (108.94, 116.44) |
| BSA | Fit | SE Fit | 95.0% CI | 95.0% PI |
|---|---|---|---|---|
| 2 | 114.1 | 0.624 | (112.76, 115.38) | (108.06, 120.08) |
| BSA | Weight | Fit | SE Fit | 95.0% CI | 95.0% PI |
|---|---|---|---|---|---|
| 2 | 92 | 112.8 | 0.448 | (111.93, 113.83) | (109.08, 116.68) |
The first output yields a predicted blood pressure of 112.7 mm Hg for a person whose weight is 92 kg based on the regression of blood pressure on weight. The second output yields a predicted blood pressure of 114.1 mm Hg for a person whose body surface area is 2 square meters based on the regression of blood pressure on body surface area. And the last output yields a predicted blood pressure of 112.8 mm Hg for a person whose body surface area is 2 square meters and whose weight is 92 kg based on the regression of blood pressure on body surface area and weight. Reviewing the confidence intervals and prediction intervals, you can see that they too yield similar results regardless of the model.
The bottom line
In short, what are the significant effects of multicollinearity on our use of a regression model to answer our research questions? In the presence of multicollinearity:
- It is okay to use an estimated regression model to predict y or estimate \(\mu_Y\) as long as you do so within the model's scope.
- We can no longer make much sense of the usual interpretation of a slope coefficient as the change in the mean response for each additional unit increases in the predictor \(x_k\) when all the other predictors are held constant.
The first point is, of course, addressed above. The second point is a direct consequence of the correlation among the predictors. It wouldn't make sense to talk about holding the values of correlated predictors constant since changing one predictor necessarily would change the values of the others.
Try it!
Correlated predictors
Effects of correlated predictor variables. This exercise reviews the impacts of multicollinearity on various aspects of regression analyses. The Allen Cognitive Level (ACL) test is designed to quantify one's cognitive abilities. David and Riley (1990) investigated the relationship of the ACL test to the level of psychopathology in a set of 69 patients from a general hospital psychiatry unit. The Allen Test data set contains the response y = ACL and three potential predictors:
- \(x_1\) = Vocab, scores on the vocabulary component of the Shipley Institute of Living Scale
- \(x_2\) = Abstract, scores on the abstraction component of the Shipley Institute of Living Scale
- \(x_3\) = SDMT, scores on the Symbol-Digit Modalities Test
-
Determine the pairwise correlations among the predictor variables to get an idea of the extent to which the predictor variables are (pairwise) correlated. (See Minitab Help: Creating a correlation matrix). Also, create a matrix plot of the data to get a visual portrayal of the relationship between the response and predictor variables. (See Minitab Help: Creating a simple matrix of scatter plots)
There’s a moderate positive correlation between each pair of predictor variables, 0.698 for \(X_1\) and \(X_2\), 0.556 for \(X_1\) and \(X_3\), and 0.577 for \(X_2\) and \(X_3\)
-
Fit the simple linear regression model with y = ACL as the response and \(x_1\) = Vocab as the predictor. After fitting your model, request that Minitab predict the response y = ACL when \(x_1\) = 25. (See Minitab Help: Performing a multiple regression analysis — with options).
- What is the value of the estimated slope coefficient \(b_1\)?
- What is the value of the standard error of \(b_1\)?
- What is the regression sum of squares, SSR (\(x_1\)), when \(x_1\) is the only predictor in the model?
- What is the predicted response of y = ACL when \(x_1\) = 25?
Estimated slope coefficient \(b_1 = 0.0298\)
Standard error \(se(b_1) = 0.0141\).
\(SSR(X_1) = 2.691\).
Predicted response when \(x_1=25\) is 4.97025.
-
Now, fit the simple linear regression model with y = ACL as the response and \(x_3\) = SDMT as the predictor. After fitting your model, request that Minitab predict the response y = ACL when \(x_3\) = 40. (See Minitab Help: Performing a multiple regression analysis — with options).
- What is the value of the estimated slope coefficient \(b_3\)?
- What is the value of the standard error of \(b_3\)?
- What is the regression sum of squares, SSR (\(x_3\)), when \(x_3\) is the only predictor in the model?
- What is the predicted response of y = ACL when \(x_3\) = 40?
Estimated slope coefficient \(b_3 = 0.02807\).
Standard error \(se(b_3) = 0.00562\).
\(SSR(X_3) = 11.68\).
Predicted response when \(x_3=40\) is 4.87634.
-
Fit the multiple linear regression model with y = ACL as the response and \(x_3\) = SDMT as the first predictor and \(x_1\) = Vocab as the second predictor. After fitting your model, request that Minitab predict the response y = ACL when \(x_1\) = 25 and \(x_3\) = 40. (See Minitab Help: Performing a multiple regression analysis — with options).
- Now, what is the value of the estimated slope coefficient \(b_1\)? and \(b_3\)?
- What is the value of the standard error of \(b_1\)? and \(b_3\)?
- What is the sequential sum of squares, SSR (\(X_1|X_3\)?
- What is the predicted response of y = ACL when \(x_1\) = 25 and \(x_3\) = 40?
Estimated slope coefficient \(b_1 = -0.0068\) (but not remotely significant).
Estimated slope coefficient \(b_3 = 0.02979\).
Standard error \(se(b_1) = 0.0150\).
Standard error \(se(b_3) = 0.00680\).
\(SSR(X_1|X_3) = 0.0979\).
Predicted response when \(x_1=25\) and \(x_3=40\) is 4.86608.
-
Summarize the effects of multicollinearity on various aspects of the regression analyses.
The regression output concerning \(X_1=Vocab\) changes considerably depending on whether \(X_3=SDMT\) is included or not. However, since \(X_1\) is not remotely significant when \(X_3\) is included, it is probably best to exclude \(X_1\) from the model. The regression output concerning \(X_3\) changes little depending on whether \(X_1\) is included or not. Multicollinearity doesn’t have a particularly adverse effect in this example.