Math & Stat Reviews
Math & Stat Reviews
Algebra
Knowledge of the following mathematical operations is required for STAT 200:
- Addition
- Subtraction
- Division
- Multiplication
- Radicals (i.e., square roots)
- Exponents
- Summations \(\left( \sum \right) \)
- Factorials (!)

Basic Statistical Concepts
These review materials are intended to provide a review of key statistical concepts and procedures. Specifically, the lesson reviews:
- populations and parameters and how they differ from samples and statistics,
- confidence intervals and their interpretation,
- hypothesis testing procedures, including the critical value approach and the P-value approach,
- chi-square analysis,
- tests of proportion, and
- power analysis.
Calculus
It is imperative that you have a working knowledge of multidimensional calculus as a prerequisite.
This includes:
- differentiation,
- integration,
- series,
- limits, and
- multivariate calculus.
Matrix Algebra
Students who do not have this foundation or have not reviewed this material within the past couple of years will struggle with the concepts and methods that build on this foundation.
Algebra Review
Algebra ReviewKnowledge of the following mathematical operations is required for STAT 200:
- Addition
- Subtraction
- Division
- Multiplication
- Radicals (i.e., square roots)
- Exponents
- Summations \(\left( \sum \right) \)
- Factorials (!)
Additionally, the ability to perform these operations in the appropriate order is necessary. Use these materials to check your understanding and preparation for taking STAT 200.
We want our students to be successful! And we know that students that do not possess a working knowledge of these topics will struggle to participate successfully in STAT 200.
Review Materials
Are you ready? As a means of helping students assess whether or not what they currently know and can do meets the expectations of instructors of STAT 200, the online program has put together a brief review of these concepts and methods. This is then followed by a short self-assessment exam that will help you determine if this prerequisite knowledge is readily available for you to apply.
Self-Assessment Procedure
- Review the concepts and methods on the pages in this section of this website.
- Download and complete the Self-Assessment Exam.
- Review the Self-Assessment Exam Solutions and determine your score.
Your score on this self-assessment should be 100%! If your score is below this you should consider further review of these materials and are strongly encouraged to take MATH 021 or an equivalent course.
If you have struggled with the methods that are presented in the self-assessment, you will indeed struggle in the courses that expect this foundation.
Note: These materials are NOT intended to be a complete treatment of the ideas and methods used in algebra. These materials and the self-assessment are simply intended as simply an 'early warning signal' for students. Also, please note that completing the self-assessment successfully does not automatically ensure success in any of the courses that use these foundation materials. Please keep in mind that this is a review only. It is not an exhaustive list of the material you need to have learned in your previous math classes. This review is meant only to be a simple guide of things you should remember and that we build upon in STAT 200.
A.1 Order of Operations
A.1 Order of OperationsWhen performing a series of mathematical operations, begin with those inside parentheses or brackets. Next, calculate any exponents or square roots. This is followed by multiplication and division, and finally, addition and subtraction.
- Parentheses
- Exponents & Square Roots
- Multiplication and Division
- Addition and Subtraction
Example A.1
Simplify: $(5+\dfrac{9}{3})^{2}$
\end{align}
Example A.2
Simplify: $\dfrac{5+6+7}{3}$
\end{align}
Example A.3
Simplify: $\dfrac{2^{2}+3^{2}+4^{2}}{3-1}$
A.2 Summations
A.2 SummationsThis is the upper-case Greek letter sigma. A sigma tells us that we need to sum (i.e., add) a series of numbers.
\[\sum\]
For example, four children are comparing how many pieces of candy they have:
| ID | Child | Pieces of Candy |
|---|---|---|
| 1 | Marty | 9 |
| 2 | Harold | 8 |
| 3 | Eugenia | 10 |
| 4 | Kevi | 8 |
We could say that: \(x_{1}=9\), \(x_{2}=8\), \(x_{3}=10\), and \(x_{4}=8\).
If we wanted to know how many total pieces of candy the group of children had, we could add the four numbers. The notation for this is:
\[\sum x_{i}\]
So, for this example, \(\sum x_{i}=9+8+10+8=35\)
To conclude, combined, the four children have 35 pieces of candy.
In statistics, some equations include the sum of all of the squared values (i.e., square each item, then add). The notation is:
\[\sum x_{i}^{2}\]
or
\[\sum (x_{i}^{2})\]
Here, \(\sum x_{i}^{2}=9^{2}+8^{2}+10^{2}+8^{2}=81+64+100+64=309\).
Sometimes we want to square a series of numbers that have already been added. The notation for this is:
\[(\sum x_{i})^{2}\]
Here,\( (\sum x_{i})^{2}=(9+8+10+8)^{2}=35^{2}=1225\)
Note that \(\sum x_{i}^{2}\) and \((\sum x_{i})^{2}\) are different.
Summations
Here is a brief review of summations as they will be applied in STAT 200:
A.3 Factorials
A.3 FactorialsFactorials are symbolized by exclamation points (!).
A factorial is a mathematical operation in which you multiply the given number by all of the positive whole numbers less than it. In other words \(n!=n \times (n-1) \times … \times 2 \times 1\).
For example,
“Four factorial” = \(4!=4\times3\times2\times1=24\)
“Six factorial” = \(6!=6\times5\times4\times3\times2\times1)=720\)
When we discuss probability distributions in STAT 200 we will see a formula that involves dividing factorials. For example,
\[\frac{3!}{2!}=\frac{3\times2\times1}{2\times1}=3\]
Here is another example,
\[\frac{6!}{2!(6-2)!}=\frac{6\times5\times4\times3\times2\times1}{(2\times1)(4\times3\times2\times1)}=\frac{6\times5}{2}=\frac{30}{2}=15\]
Also, note that 0! = 1
Factorials
Here is a brief review of factorials as they will be applied in STAT 200:
A.4 Self-Assess
A.4 Self-AssessSelf-Assessment Procedure
- Review the concepts and methods on the pages in this section of this website.
- Download and Complete the STAT 200 Algebra Self-Assessment
- Determine your Score by Reviewing the STAT 200 Algebra Self-Assessment: Solutions.
Your score on this self-assessment should be 100%! If your score is below this you should consider further review of these materials and are strongly encouraged to take MATH 021 or an equivalent course.
If you have struggled with the methods that are presented in the self assessment, you will indeed struggle in the courses above that expect this foundation.
Note: These materials are NOT intended to be a complete treatment of the ideas and methods used in these algebra methods. These materials and the accompanying self-assessment are simply intended as simply an 'early warning signal' for students. Also, please note that completing the self-assessment successfully does not automatically ensure success in any of the courses that use this foundation.
Basic Statistical Concepts
Basic Statistical ConceptsThe Prerequisites Checklist page on the Department of Statistics website lists a number of courses that require a foundation of basic statistical concepts as a prerequisite. All of the graduate courses in the Master of Applied Statistics program heavily rely on these concepts and procedures. Therefore, it is imperative — after you study and work through this lesson — that you thoroughly understand all the material presented here. Students that do not possess a firm understanding of these basic concepts will struggle to participate successfully in any of the graduate-level courses above STAT 500. Courses such as STAT 501 - Regression Methods or STAT 502 - Analysis of Variance and Design of Experiments require and build from this foundation.
Review Materials
These review materials are intended to provide a review of key statistical concepts and procedures. Specifically, the lesson reviews:
- populations and parameters and how they differ from samples and statistics,
- confidence intervals and their interpretation,
- hypothesis testing procedures, including the critical value approach and the P-value approach,
- chi-square analysis,
- tests of proportion, and
- power analysis.
For instance, with regards to hypothesis testing, some of you may have learned only one approach — some the P-value approach, and some the critical value approach. It is important that you understand both approaches. If the P-value approach is new to you, you might have to spend a little more time on this lesson than if not.
Learning Objectives & Outcomes
Upon completion of this review of basic statistical concepts, you should be able to do the following:
-
Distinguish between a population and a sample.
-
Distinguish between a parameter and a statistic.
-
Understand the basic concept and the interpretation of a confidence interval.
-
Know the general form of most confidence intervals.
-
Be able to calculate a confidence interval for a population mean µ.
-
Understand how different factors affect the length of the t-interval for the population mean µ.
-
Understand the general idea of hypothesis testing -- especially how the basic procedure is similar to that followed for criminal trials conducted in the United States.
-
Be able to distinguish between the two types of errors that can occur whenever a hypothesis test is conducted.
-
Understand the basic procedures for the critical value approach to hypothesis testing. Specifically, be able to conduct a hypothesis test for the population mean µ using the critical value approach.
-
Understand the basic procedures for the P-value approach to hypothesis testing. Specifically, be able to conduct a hypothesis test for the population mean µ using the P-value approach.
- Understand the basic procedures for testing the independence of two categorical variables using a Chi-square test of independence.
- Be able to determine if a test contains enough power to make a reasonable conclusion using power analysis.
- Be able to use power analysis to calculate the number of samples required to achieve a specified level of power.
- Understand how a test of proportion can be used to assess whether a sample from a population represents the true proportion of the entire population.
Self-Assessment Procedure
- Review the concepts and methods on the pages in this section of this website.
- Download and complete the Self-Assessment Exam at the end of this section.
- Review the Self-Assessment Exam Solutions and determine your score.
A score below 70% suggests that the concepts and procedures that are covered in STAT 500 have not been mastered adequately. Students are strongly encouraged to take STAT 500, thoroughly review the materials that are covered in the sections above or take additional coursework that focuses on these foundations.
If you have struggled with the concepts and methods that are presented here, you will indeed struggle in any of the graduate-level courses included in the Master of Applied Statistics program above STAT 500 that expect and build on this foundation.
S.1 Basic Terminology
S.1 Basic TerminologyPopulation and Parameters
- Population
- A population is any large collection of objects or individuals, such as Americans, students, or trees about which information is desired.
- Parameter
- A parameter is any summary number, like an average or percentage, that describes the entire population.
The population mean \(\mu\) (the greek letter "mu") and the population proportion p are two different population parameters. For example:
- We might be interested in learning about \(\mu\), the average weight of all middle-aged female Americans. The population consists of all middle-aged female Americans, and the parameter is µ.
- Or, we might be interested in learning about p, the proportion of likely American voters approving of the president's job performance. The population comprises all likely American voters, and the parameter is p.
The problem is that 99.999999999999... % of the time, we don't — or can't — know the real value of a population parameter. The best we can do is estimate the parameter! This is where samples and statistics come in to play.
Samples and statistics
- Sample
- A sample is a representative group drawn from the population.
- Statistic
- A statistic is any summary number, like an average or percentage, that describes the sample.
The sample mean, \(\bar{x}\), and the sample proportion \(\hat{p}\) are two different sample statistics. For example:
- We might use \(\bar{x}\), the average weight of a random sample of 100 middle-aged female Americans, to estimate µ, the average weight of all middle-aged female Americans.
- Or, we might use \(\hat{p}\), the proportion in a random sample of 1000 likely American voters who approve of the president's job performance, to estimate p, the proportion of all likely American voters who approve of the president's job performance.
Because samples are manageable in size, we can determine the actual value of any statistic. We use the known value of the sample statistic to learn about the unknown value of the population parameter.
Example S.1.1
What was the prevalence of smoking at Penn State University before the 'no smoking' policy?
The main campus at Penn State University has a population of approximately 42,000 students. A research question is "What proportion of these students smoke regularly?" A survey was administered to a sample of 987 Penn State students. Forty-three percent (43%) of the sampled students reported that they smoked regularly. How confident can we be that 43% is close to the actual proportion of all Penn State students who smoke?
- The population is all 42,000 students at Penn State University.
- The parameter of interest is p, the proportion of students at Penn State University who smoke regularly.
- The sample is a random selection of 987 students at Penn State University.
- The statistic is the proportion, \(\hat{p}\), of the sample of 987 students who smoke regularly. The value of the sample proportion is 0.43.
Example S.1.2
Are the grades of college students inflated?
Let's suppose that there exists a population of 7 million college students in the United States today. (The actual number depends on how you define "college student.") And, let's assume that the average GPA of all of these college students is 2.7 (on a 4-point scale). If we take a random sample of 100 college students, how likely is it that the sampled 100 students would have an average GPA as large as 2.9 if the population average was 2.7?
- The population is equal to all 7 million college students in the United States today.
- The parameter of interest is µ, the average GPA of all college students in the United States today.
- The sample is a random selection of 100 college students in the United States.
- The statistic is the mean grade point average, \(\bar{x}\), of the sample of 100 college students. The value of the sample mean is 2.9.
Example S.1.3
Is there a linear relationship between birth weight and length of gestation?
Consider the relationship between the birth weight of a baby and the length of its gestation:
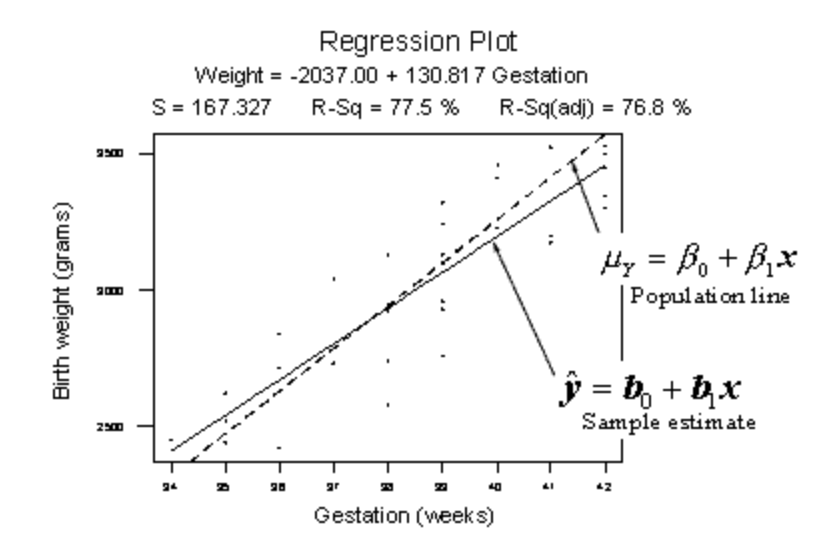
The dashed line summarizes the (unknown) relationship —\(\mu_Y = \beta_0+\beta_1x\)— between birth weight and gestation length of all births in the population. The solid line summarizes the relationship —\(\hat{y} = \beta_0+\beta_1x\)— between birth weight and gestation length in our random sample of 32 births. The goal of linear regression analysis is to use the solid line (the sample) in hopes of learning about the dashed line (the population).
Next... Confidence intervals and hypothesis tests
There are two ways to learn about a population parameter.
1) We can use confidence intervals to estimate parameters.
"We can be 95% confident that the proportion of Penn State students who have a tattoo is between 5.1% and 15.3%."
2) We can use hypothesis tests to test and ultimately draw conclusions about the value of a parameter.
"There is enough statistical evidence to conclude that the mean normal body temperature of adults is lower than 98.6 degrees F."
We review these two methods in the next two sections.
S.2 Confidence Intervals
S.2 Confidence IntervalsLet's review the basic concept of a confidence interval.
Suppose we want to estimate an actual population mean \(\mu\). As you know, we can only obtain \(\bar{x}\), the mean of a sample randomly selected from the population of interest. We can use \(\bar{x}\) to find a range of values:
\[\text{Lower value} < \text{population mean}\;\; \mu < \text{Upper value}\]
that we can be really confident contains the population mean \(\mu\). The range of values is called a "confidence interval."
Example S.2.1
Should using a hand-held cell phone while driving be illegal?
There is little doubt that you have seen numerous confidence intervals for population proportions reported in newspapers over the years.
For example, a newspaper report (ABC News poll, May 16-20, 2001) was concerned about whether or not U.S. adults thought using a hand-held cell phone while driving should be illegal. Of the 1,027 U.S. adults randomly selected for participation in the poll, 69% believed it should be illegal. The reporter claimed that the poll's "margin of error" was 3%. Therefore, the confidence interval for the (unknown) population proportion p is 69% ± 3%. That is, we can be really confident that between 66% and 72% of all U.S. adults think using a hand-held cell phone while driving a car should be illegal.
General Form of (Most) Confidence Intervals
The previous example illustrates the general form of most confidence intervals, namely:
$\text{Sample estimate} \pm \text{margin of error}$
The lower limit is obtained by:
$\text{the lower limit L of the interval} = \text{estimate} - \text{margin of error}$
The upper limit is obtained by:
$\text{the upper limit U of the interval} = \text{estimate} + \text{margin of error}$
Once we've obtained the interval, we can claim that we are really confident that the value of the population parameter is somewhere between the value of L and the value of U.
So far, we've been very general in our discussion of the calculation and interpretation of confidence intervals. To be more specific about their use, let's consider a specific interval, namely the "t-interval for a population mean µ."
(1-α)100% t-interval for the population mean \(\mu\)
If we are interested in estimating a population mean \(\mu\), it is very likely that we would use the t-interval for a population mean \(\mu\).
- t-Interval for a Population Mean
- The formula for the confidence interval in words is:
$\text{Sample mean} \pm (\text{t-multiplier} \times \text{standard error})$
- and you might recall that the formula for the confidence interval in notation is:
- $\bar{x}\pm t_{\alpha/2, n-1}\left(\dfrac{s}{\sqrt{n}}\right)$
Note that:
- the "t-multiplier," which we denote as \(t_{\alpha/2, n-1}\), depends on the sample size through n - 1 (called the "degrees of freedom") and the confidence level \((1-\alpha)\times100%\) through \(\frac{\alpha}{2}\).
- the "standard error," which is \(\frac{s}{\sqrt{n}}\), quantifies how much the sample means \(\bar{x}\) vary from sample to sample. That is, the standard error is just another name for the estimated standard deviation of all the possible sample means.
- the quantity to the right of the ± sign, i.e., "t-multiplier × standard error," is just a more specific form of the margin of error. That is, the margin of error in estimating a population mean µ is calculated by multiplying the t-multiplier by the standard error of the sample mean.
- the formula is only appropriate if a certain assumption is met, namely that the data are normally distributed.
Clearly, the sample mean \(\bar{x}\), the sample standard deviation s, and the sample size n are all readily obtained from the sample data. Now, we need to review how to obtain the value of the t-multiplier, and we'll be all set.
How is the t-multiplier determined?
As the following graph illustrates, we put the confidence level $1-\alpha$ in the center of the t-distribution. Then, since the entire probability represented by the curve must equal 1, a probability of α must be shared equally among the two "tails" of the distribution. That is, the probability of the left tail is $\frac{\alpha}{2}$ and the probability of the right tail is $\frac{\alpha}{2}$. If we add up the probabilities of the various parts $(\frac{\alpha}{2} + 1-\alpha + \frac{\alpha}{2})$, we get 1. The t-multiplier, denoted \(t_{\alpha/2}\), is the t-value such that the probability "to the right of it" is $\frac{\alpha}{2}$:
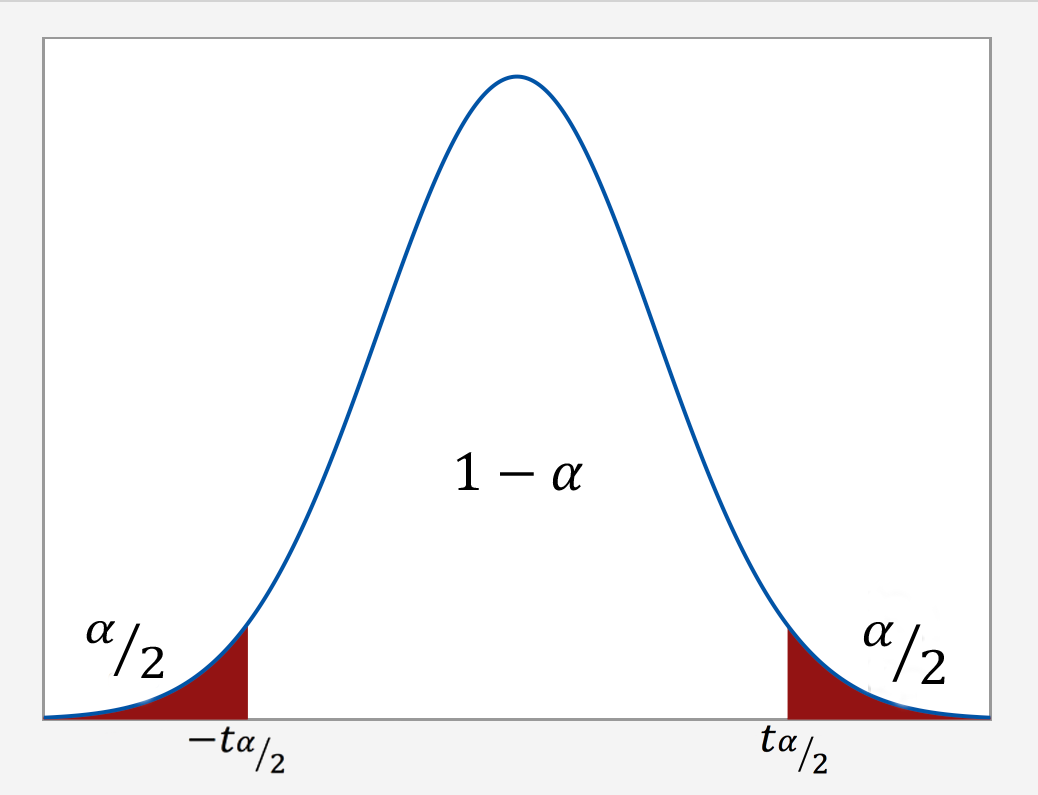
It should be no surprise that we want to be as confident as possible when we estimate a population parameter. This is why confidence levels are typically very high. The most common confidence levels are 90%, 95%, and 99%. The following table contains a summary of the values of \(\frac{\alpha}{2}\) corresponding to these common confidence levels. (Note that the"confidence coefficient" is merely the confidence level reported as a proportion rather than as a percentage.)
| Confidence Coefficient $(1-\alpha)$ | Confidence Level $(1-\alpha) \times 100$ | $(1-\dfrac{\alpha}{2})$ | $\dfrac{\alpha}{2}$ |
|---|---|---|---|
| 0.90 | 90% | 0.95 | 0.05 |
| 0.95 | 95% | 0.975 | 0.025 |
| 0.99 | 99% | 0.995 | 0.005 |
Minitab® – Using Software
The good news is that statistical software, such as Minitab, will calculate most confidence intervals for us.
Let's take an example of researchers who are interested in the average heart rate of male college students. Assume a random sample of 130 male college students were taken for the study.
The following is the Minitab Output of a one-sample t-interval output using this data.
One-Sample T: Heart Rate
Descriptive Statistics
| N | Mean | StDev | SE Mean | 95% CI for $\mu$ |
|---|---|---|---|---|
| 130 | 73.762 | 7.062 | 0.619 | (72.536, 74.987) |
$\mu$: mean of HR
In this example, the researchers were interested in estimating \(\mu\), the heart rate. The output indicates that the mean for the sample of n = 130 male students equals 73.762. The sample standard deviation (StDev) is 7.062 and the estimated standard error of the mean (SE Mean) is 0.619. The 95% confidence interval for the population mean $\mu$ is (72.536, 74.987). We can be 95% confident that the mean heart rate of all male college students is between 72.536 and 74.987 beats per minute.
Factors Affecting the Width of the t-interval for the Mean $\mu$
Think about the width of the interval in the previous example. In general, do you think we desire narrow confidence intervals or wide confidence intervals? If you are not sure, consider the following two intervals:
- We are 95% confident that the average GPA of all college students is between 1.0 and 4.0.
- We are 95% confident that the average GPA of all college students is between 2.7 and 2.9.
Which of these two intervals is more informative? Of course, the narrower one gives us a better idea of the magnitude of the true unknown average GPA. In general, the narrower the confidence interval, the more information we have about the value of the population parameter. Therefore, we want all of our confidence intervals to be as narrow as possible. So, let's investigate what factors affect the width of the t-interval for the mean \(\mu\).
Of course, to find the width of the confidence interval, we just take the difference in the two limits:
Width = Upper Limit - Lower Limit
What factors affect the width of the confidence interval? We can examine this question by using the formula for the confidence interval and seeing what would happen should one of the elements of the formula be allowed to vary.
\[\bar{x}\pm t_{\alpha/2, n-1}\left(\dfrac{s}{\sqrt{n}}\right)\]
What is the width of the t-interval for the mean? If you subtract the lower limit from the upper limit, you get:
\[\text{Width }=2 \times t_{\alpha/2, n-1}\left(\dfrac{s}{\sqrt{n}}\right)\]
Now, let's investigate the factors that affect the length of this interval. Convince yourself that each of the following statements is accurate:
- As the sample mean increases, the length stays the same. That is, the sample mean plays no role in the width of the interval.
- As the sample standard deviation s decreases, the width of the interval decreases. Since s is an estimate of how much the data vary naturally, we have little control over s other than making sure that we make our measurements as carefully as possible.
- As we decrease the confidence level, the t-multiplier decreases, and hence the width of the interval decreases. In practice, we wouldn't want to set the confidence level below 90%.
- As we increase the sample size, the width of the interval decreases. This is the factor that we have the most flexibility in changing, the only limitation being our time and financial constraints.
In Closing
In our review of confidence intervals, we have focused on just one confidence interval. The important thing to recognize is that the topics discussed here — the general form of intervals, determination of t-multipliers, and factors affecting the width of an interval — generally extend to all of the confidence intervals we will encounter in this course.
S.3 Hypothesis Testing
S.3 Hypothesis TestingIn reviewing hypothesis tests, we start first with the general idea. Then, we keep returning to the basic procedures of hypothesis testing, each time adding a little more detail.
The general idea of hypothesis testing involves:
- Making an initial assumption.
- Collecting evidence (data).
- Based on the available evidence (data), deciding whether to reject or not reject the initial assumption.
Every hypothesis test — regardless of the population parameter involved — requires the above three steps.
Example S.3.1
Is Normal Body Temperature Really 98.6 Degrees F?
Consider the population of many, many adults. A researcher hypothesized that the average adult body temperature is lower than the often-advertised 98.6 degrees F. That is, the researcher wants an answer to the question: "Is the average adult body temperature 98.6 degrees? Or is it lower?" To answer his research question, the researcher starts by assuming that the average adult body temperature was 98.6 degrees F.
Then, the researcher went out and tried to find evidence that refutes his initial assumption. In doing so, he selects a random sample of 130 adults. The average body temperature of the 130 sampled adults is 98.25 degrees.
Then, the researcher uses the data he collected to make a decision about his initial assumption. It is either likely or unlikely that the researcher would collect the evidence he did given his initial assumption that the average adult body temperature is 98.6 degrees:
- If it is likely, then the researcher does not reject his initial assumption that the average adult body temperature is 98.6 degrees. There is not enough evidence to do otherwise.
- If it is unlikely, then:
- either the researcher's initial assumption is correct and he experienced a very unusual event;
- or the researcher's initial assumption is incorrect.
In statistics, we generally don't make claims that require us to believe that a very unusual event happened. That is, in the practice of statistics, if the evidence (data) we collected is unlikely in light of the initial assumption, then we reject our initial assumption.
Example S.3.2
Criminal Trial Analogy
One place where you can consistently see the general idea of hypothesis testing in action is in criminal trials held in the United States. Our criminal justice system assumes "the defendant is innocent until proven guilty." That is, our initial assumption is that the defendant is innocent.
In the practice of statistics, we make our initial assumption when we state our two competing hypotheses -- the null hypothesis (H0) and the alternative hypothesis (HA). Here, our hypotheses are:
- H0: Defendant is not guilty (innocent)
- HA: Defendant is guilty
In statistics, we always assume the null hypothesis is true. That is, the null hypothesis is always our initial assumption.
The prosecution team then collects evidence — such as finger prints, blood spots, hair samples, carpet fibers, shoe prints, ransom notes, and handwriting samples — with the hopes of finding "sufficient evidence" to make the assumption of innocence refutable.
In statistics, the data are the evidence.
The jury then makes a decision based on the available evidence:
- If the jury finds sufficient evidence — beyond a reasonable doubt — to make the assumption of innocence refutable, the jury rejects the null hypothesis and deems the defendant guilty. We behave as if the defendant is guilty.
- If there is insufficient evidence, then the jury does not reject the null hypothesis. We behave as if the defendant is innocent.
In statistics, we always make one of two decisions. We either "reject the null hypothesis" or we "fail to reject the null hypothesis."
Errors in Hypothesis Testing
Did you notice the use of the phrase "behave as if" in the previous discussion? We "behave as if" the defendant is guilty; we do not "prove" that the defendant is guilty. And, we "behave as if" the defendant is innocent; we do not "prove" that the defendant is innocent.
This is a very important distinction! We make our decision based on evidence not on 100% guaranteed proof. Again:
- If we reject the null hypothesis, we do not prove that the alternative hypothesis is true.
- If we do not reject the null hypothesis, we do not prove that the null hypothesis is true.
We merely state that there is enough evidence to behave one way or the other. This is always true in statistics! Because of this, whatever the decision, there is always a chance that we made an error.
Let's review the two types of errors that can be made in criminal trials:
| Jury Decision | Truth | ||
|---|---|---|---|
| Not Guilty | Guilty | ||
| Not Guilty | OK | ERROR | |
| Guilty | ERROR | OK | |
Table S.3.2 shows how this corresponds to the two types of errors in hypothesis testing.
| Decision | Truth | ||
|---|---|---|---|
| Null Hypothesis | Alternative Hypothesis | ||
| Do not Reject Null | OK | Type II Error | |
| Reject Null | Type I Error | OK | |
Note that, in statistics, we call the two types of errors by two different names -- one is called a "Type I error," and the other is called a "Type II error." Here are the formal definitions of the two types of errors:
- Type I Error
- The null hypothesis is rejected when it is true.
- Type II Error
- The null hypothesis is not rejected when it is false.
There is always a chance of making one of these errors. But, a good scientific study will minimize the chance of doing so!
Making the Decision
Recall that it is either likely or unlikely that we would observe the evidence we did given our initial assumption. If it is likely, we do not reject the null hypothesis. If it is unlikely, then we reject the null hypothesis in favor of the alternative hypothesis. Effectively, then, making the decision reduces to determining "likely" or "unlikely."
In statistics, there are two ways to determine whether the evidence is likely or unlikely given the initial assumption:
- We could take the "critical value approach" (favored in many of the older textbooks).
- Or, we could take the "P-value approach" (what is used most often in research, journal articles, and statistical software).
In the next two sections, we review the procedures behind each of these two approaches. To make our review concrete, let's imagine that μ is the average grade point average of all American students who major in mathematics. We first review the critical value approach for conducting each of the following three hypothesis tests about the population mean $\mu$:
|
Type
|
Null
|
Alternative
|
|---|---|---|
|
Right-tailed
|
H0 : μ = 3
|
HA : μ > 3
|
|
Left-tailed
|
H0 : μ = 3
|
HA : μ < 3
|
|
Two-tailed
|
H0 : μ = 3
|
HA : μ ≠ 3
|
In Practice
-
We would want to conduct the first hypothesis test if we were interested in concluding that the average grade point average of the group is more than 3.
-
We would want to conduct the second hypothesis test if we were interested in concluding that the average grade point average of the group is less than 3.
-
And, we would want to conduct the third hypothesis test if we were only interested in concluding that the average grade point average of the group differs from 3 (without caring whether it is more or less than 3).
Upon completing the review of the critical value approach, we review the P-value approach for conducting each of the above three hypothesis tests about the population mean \(\mu\). The procedures that we review here for both approaches easily extend to hypothesis tests about any other population parameter.
S.3.1 Hypothesis Testing (Critical Value Approach)
S.3.1 Hypothesis Testing (Critical Value Approach)The critical value approach involves determining "likely" or "unlikely" by determining whether or not the observed test statistic is more extreme than would be expected if the null hypothesis were true. That is, it entails comparing the observed test statistic to some cutoff value, called the "critical value." If the test statistic is more extreme than the critical value, then the null hypothesis is rejected in favor of the alternative hypothesis. If the test statistic is not as extreme as the critical value, then the null hypothesis is not rejected.
Specifically, the four steps involved in using the critical value approach to conducting any hypothesis test are:
- Specify the null and alternative hypotheses.
- Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. To conduct the hypothesis test for the population mean μ, we use the t-statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t-distribution with n - 1 degrees of freedom.
- Determine the critical value by finding the value of the known distribution of the test statistic such that the probability of making a Type I error — which is denoted \(\alpha\) (greek letter "alpha") and is called the "significance level of the test" — is small (typically 0.01, 0.05, or 0.10).
- Compare the test statistic to the critical value. If the test statistic is more extreme in the direction of the alternative than the critical value, reject the null hypothesis in favor of the alternative hypothesis. If the test statistic is less extreme than the critical value, do not reject the null hypothesis.
Example S.3.1.1
Mean GPA
In our example concerning the mean grade point average, suppose we take a random sample of n = 15 students majoring in mathematics. Since n = 15, our test statistic t* has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.
Right-Tailed
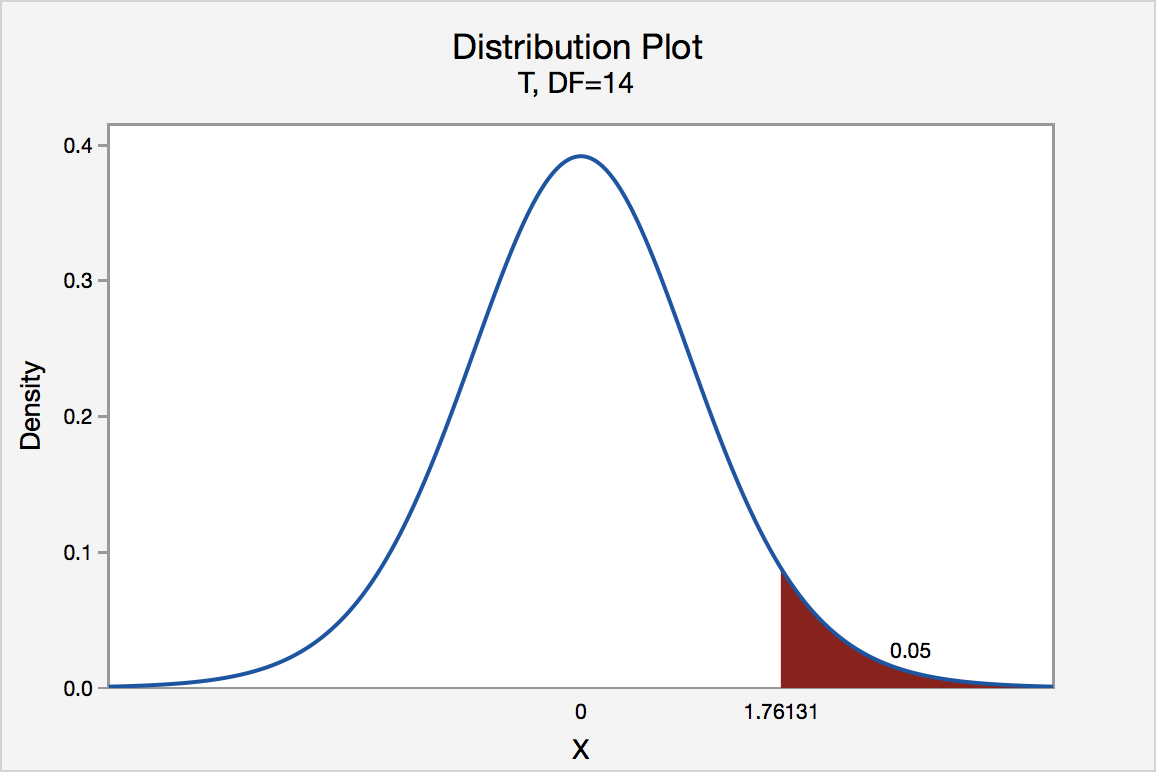
The critical value for conducting the right-tailed test H0 : μ = 3 versus HA : μ > 3 is the t-value, denoted t\(\alpha\), n - 1, such that the probability to the right of it is \(\alpha\). It can be shown using either statistical software or a t-table that the critical value t 0.05,14 is 1.7613. That is, we would reject the null hypothesis H0 : μ = 3 in favor of the alternative hypothesis HA : μ > 3 if the test statistic t* is greater than 1.7613. Visually, the rejection region is shaded red in the graph.
Left-Tailed
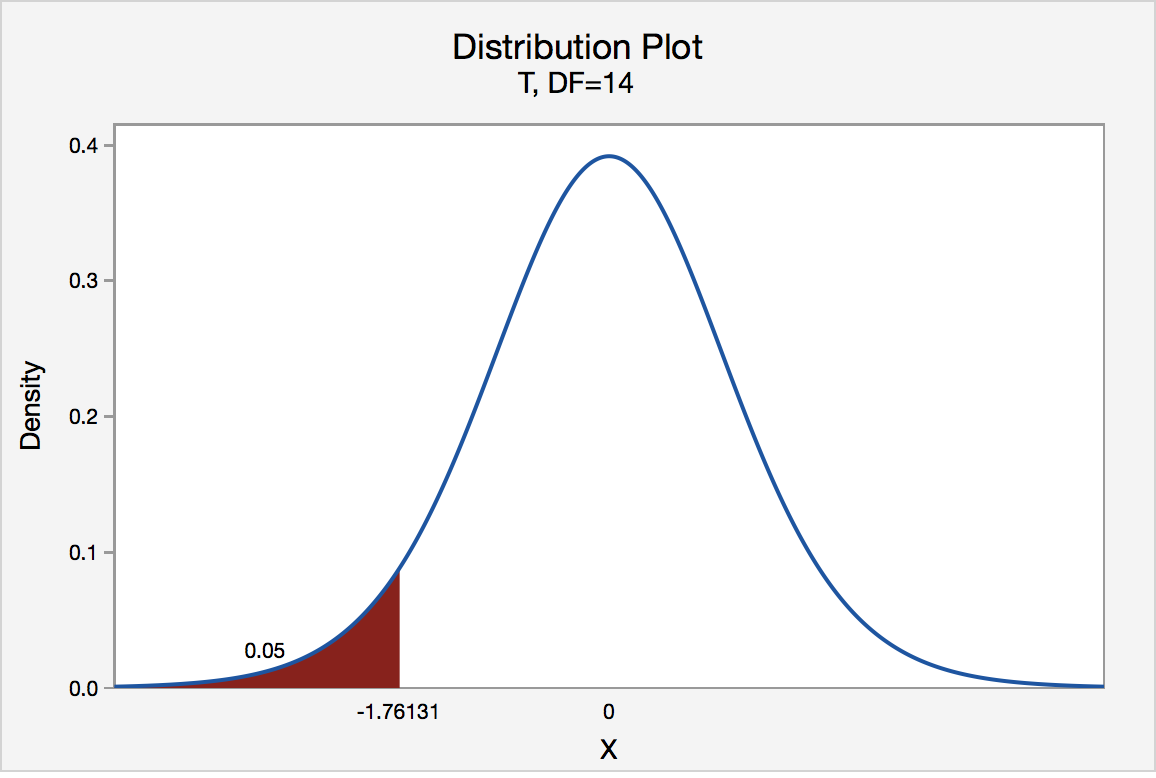
The critical value for conducting the left-tailed test H0 : μ = 3 versus HA : μ < 3 is the t-value, denoted -t(\(\alpha\), n - 1), such that the probability to the left of it is \(\alpha\). It can be shown using either statistical software or a t-table that the critical value -t0.05,14 is -1.7613. That is, we would reject the null hypothesis H0 : μ = 3 in favor of the alternative hypothesis HA : μ < 3 if the test statistic t* is less than -1.7613. Visually, the rejection region is shaded red in the graph.
Two-Tailed
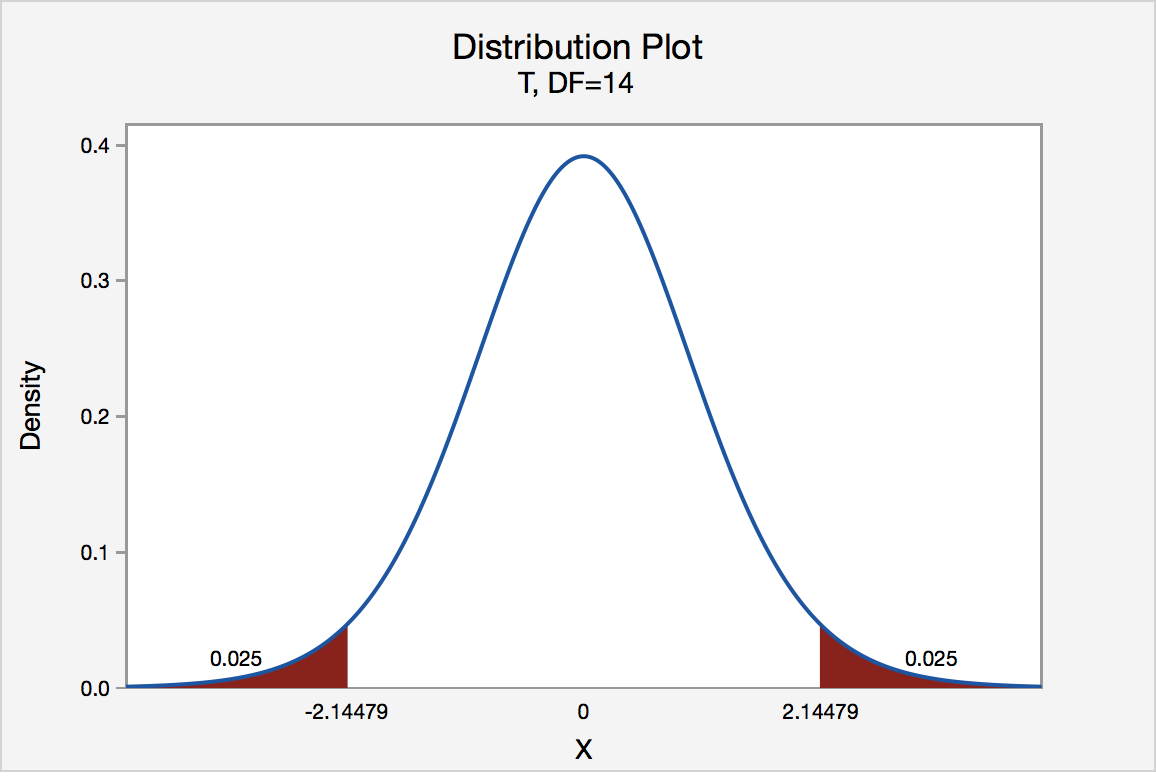
There are two critical values for the two-tailed test H0 : μ = 3 versus HA : μ ≠ 3 — one for the left-tail denoted -t(\(\alpha\)/2, n - 1) and one for the right-tail denoted t(\(\alpha\)/2, n - 1). The value -t(\(\alpha\)/2, n - 1) is the t-value such that the probability to the left of it is \(\alpha\)/2, and the value t(\(\alpha\)/2, n - 1) is the t-value such that the probability to the right of it is \(\alpha\)/2. It can be shown using either statistical software or a t-table that the critical value -t0.025,14 is -2.1448 and the critical value t0.025,14 is 2.1448. That is, we would reject the null hypothesis H0 : μ = 3 in favor of the alternative hypothesis HA : μ ≠ 3 if the test statistic t* is less than -2.1448 or greater than 2.1448. Visually, the rejection region is shaded red in the graph.
S.3.2 Hypothesis Testing (P-Value Approach)
S.3.2 Hypothesis Testing (P-Value Approach)The P-value approach involves determining "likely" or "unlikely" by determining the probability — assuming the null hypothesis was true — of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed. If the P-value is small, say less than (or equal to) \(\alpha\), then it is "unlikely." And, if the P-value is large, say more than \(\alpha\), then it is "likely."
If the P-value is less than (or equal to) \(\alpha\), then the null hypothesis is rejected in favor of the alternative hypothesis. And, if the P-value is greater than \(\alpha\), then the null hypothesis is not rejected.
Specifically, the four steps involved in using the P-value approach to conducting any hypothesis test are:
- Specify the null and alternative hypotheses.
- Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. Again, to conduct the hypothesis test for the population mean μ, we use the t-statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t-distribution with n - 1 degrees of freedom.
- Using the known distribution of the test statistic, calculate the P-value: "If the null hypothesis is true, what is the probability that we'd observe a more extreme test statistic in the direction of the alternative hypothesis than we did?" (Note how this question is equivalent to the question answered in criminal trials: "If the defendant is innocent, what is the chance that we'd observe such extreme criminal evidence?")
- Set the significance level, \(\alpha\), the probability of making a Type I error to be small — 0.01, 0.05, or 0.10. Compare the P-value to \(\alpha\). If the P-value is less than (or equal to) \(\alpha\), reject the null hypothesis in favor of the alternative hypothesis. If the P-value is greater than \(\alpha\), do not reject the null hypothesis.
Example S.3.2.1
Mean GPA
In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t* equaling 2.5. Since n = 15, our test statistic t* has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.
Right Tailed
The P-value for conducting the right-tailed test H0 : μ = 3 versus HA : μ > 3 is the probability that we would observe a test statistic greater than t* = 2.5 if the population mean \(\mu\) really were 3. Recall that probability equals the area under the probability curve. The P-value is therefore the area under a tn - 1 = t14 curve and to the right of the test statistic t* = 2.5. It can be shown using statistical software that the P-value is 0.0127. The graph depicts this visually.
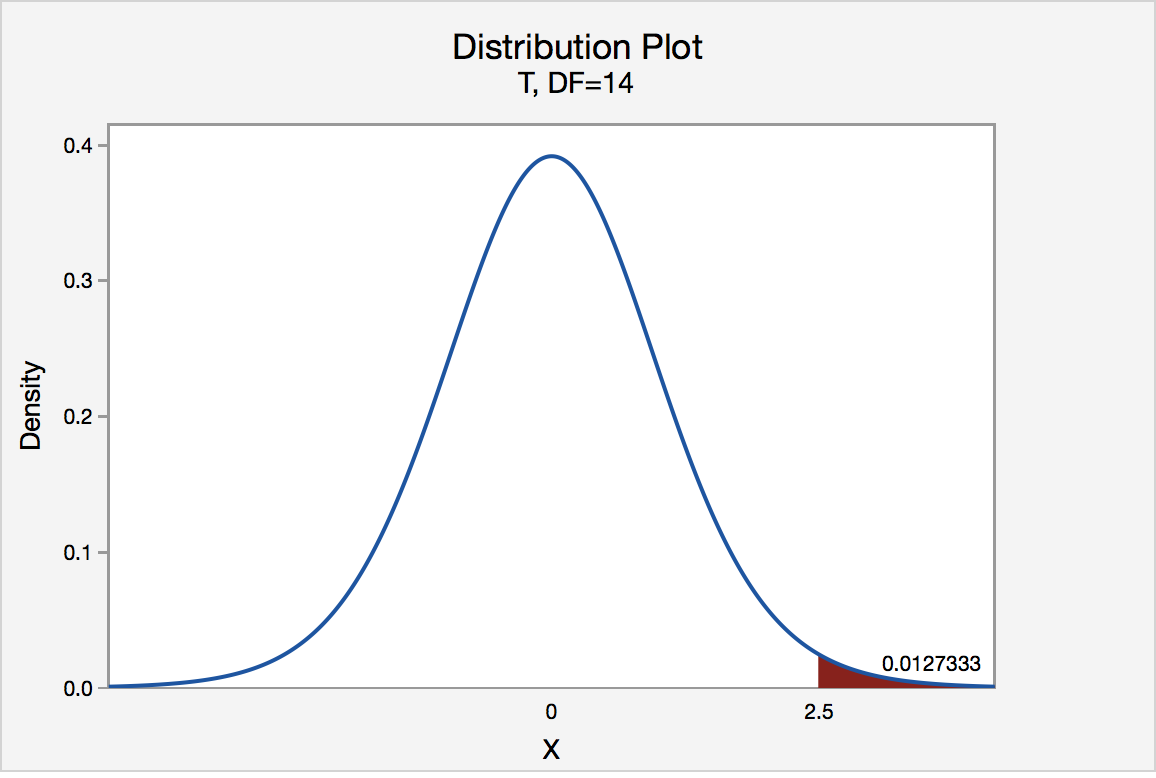
The P-value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t* in the direction of HA if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P-value, 0.0127, is less than \(\alpha\) = 0.05, we reject the null hypothesis H0 : μ = 3 in favor of the alternative hypothesis HA : μ > 3.
Note that we would not reject H0 : μ = 3 in favor of HA : μ > 3 if we lowered our willingness to make a Type I error to \(\alpha\) = 0.01 instead, as the P-value, 0.0127, is then greater than \(\alpha\) = 0.01.
Left Tailed
In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t* instead of equaling -2.5. The P-value for conducting the left-tailed test H0 : μ = 3 versus HA : μ < 3 is the probability that we would observe a test statistic less than t* = -2.5 if the population mean μ really were 3. The P-value is therefore the area under a tn - 1 = t14 curve and to the left of the test statistic t* = -2.5. It can be shown using statistical software that the P-value is 0.0127. The graph depicts this visually.
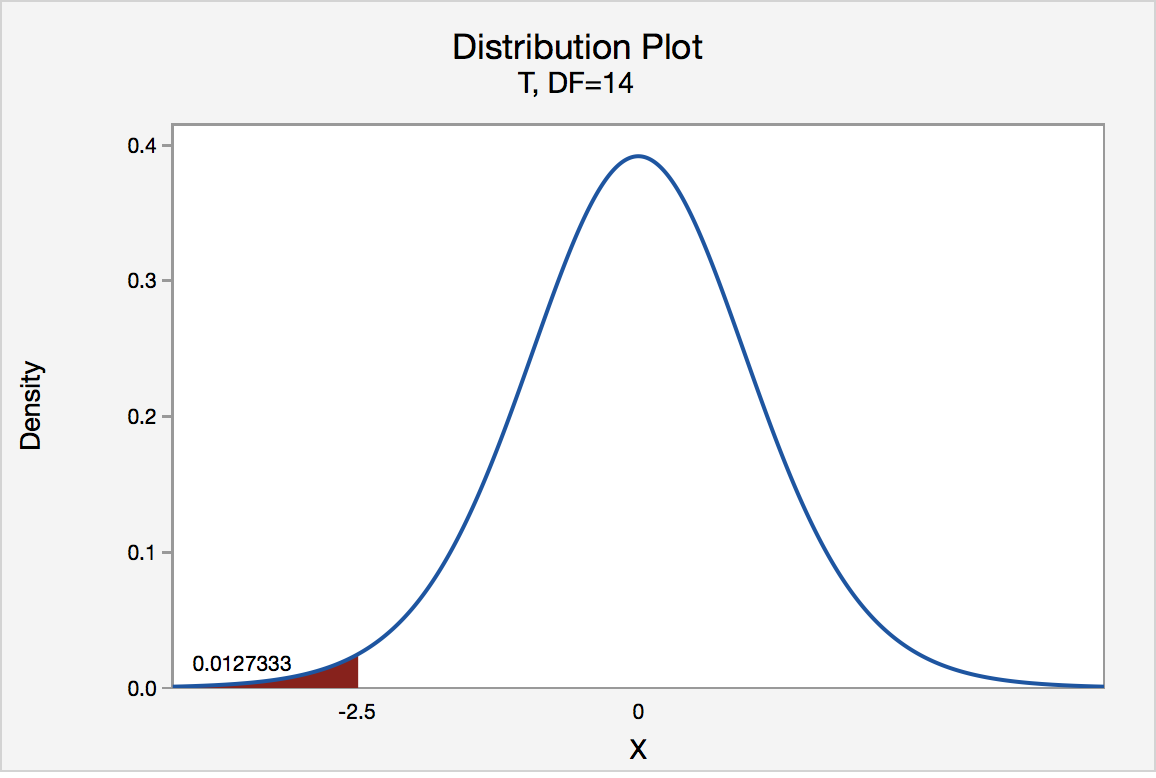
The P-value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t* in the direction of HA if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P-value, 0.0127, is less than α = 0.05, we reject the null hypothesis H0 : μ = 3 in favor of the alternative hypothesis HA : μ < 3.
Note that we would not reject H0 : μ = 3 in favor of HA : μ < 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P-value, 0.0127, is then greater than \(\alpha\) = 0.01.
Two-Tailed
In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t* instead of equaling -2.5. The P-value for conducting the two-tailed test H0 : μ = 3 versus HA : μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean μ really was 3. That is, the two-tailed test requires taking into account the possibility that the test statistic could fall into either tail (hence the name "two-tailed" test). The P-value is, therefore, the area under a tn - 1 = t14 curve to the left of -2.5 and to the right of 2.5. It can be shown using statistical software that the P-value is 0.0127 + 0.0127, or 0.0254. The graph depicts this visually.
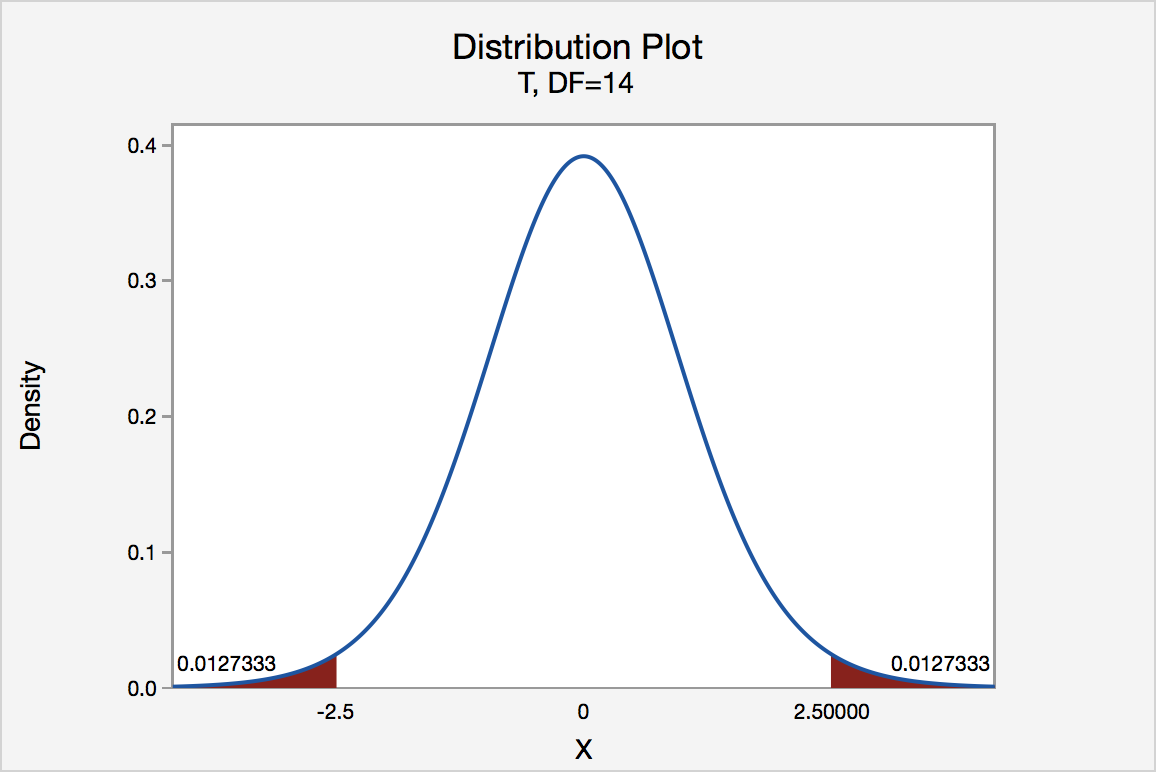
Note that the P-value for a two-tailed test is always two times the P-value for either of the one-tailed tests. The P-value, 0.0254, tells us it is "unlikely" that we would observe such an extreme test statistic t* in the direction of HA if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P-value, 0.0254, is less than α = 0.05, we reject the null hypothesis H0 : μ = 3 in favor of the alternative hypothesis HA : μ ≠ 3.
Note that we would not reject H0 : μ = 3 in favor of HA : μ ≠ 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P-value, 0.0254, is then greater than \(\alpha\) = 0.01.
Now that we have reviewed the critical value and P-value approach procedures for each of the three possible hypotheses, let's look at three new examples — one of a right-tailed test, one of a left-tailed test, and one of a two-tailed test.
The good news is that, whenever possible, we will take advantage of the test statistics and P-values reported in statistical software, such as Minitab, to conduct our hypothesis tests in this course.
S.3.3 Hypothesis Testing Examples
S.3.3 Hypothesis Testing ExamplesBrinell Hardness Scores
An engineer measured the Brinell hardness of 25 pieces of ductile iron that were subcritically annealed. The resulting data were:
| Brinell Hardness of 25 Pieces of Ductile Iron | ||||||||
|---|---|---|---|---|---|---|---|---|
| 170 | 167 | 174 | 179 | 179 | 187 | 179 | 183 | 179 |
| 156 | 163 | 156 | 187 | 156 | 167 | 156 | 174 | 170 |
| 183 | 179 | 174 | 179 | 170 | 159 | 187 | ||
The engineer hypothesized that the mean Brinell hardness of all such ductile iron pieces is greater than 170. Therefore, he was interested in testing the hypotheses:
H0 : μ = 170
HA : μ > 170
The engineer entered his data into Minitab and requested that the "one-sample t-test" be conducted for the above hypotheses. He obtained the following output:
Descriptive Statistics
| N | Mean | StDev | SE Mean | 95% Lower Bound |
|---|---|---|---|---|
| 25 | 172.52 | 10.31 | 2.06 | 168.99 |
$\mu$: mean of Brinelli
Test
Null hypothesis H₀: $\mu$ = 170
Alternative hypothesis H₁: $\mu$ > 170
| T-Value | P-Value |
|---|---|
| 1.22 | 0.117 |
The output tells us that the average Brinell hardness of the n = 25 pieces of ductile iron was 172.52 with a standard deviation of 10.31. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 10.31 by the square root of n = 25, is 2.06). The test statistic t* is 1.22, and the P-value is 0.117.
If the engineer set his significance level α at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t* were greater than 1.7109 (determined using statistical software or a t-table):
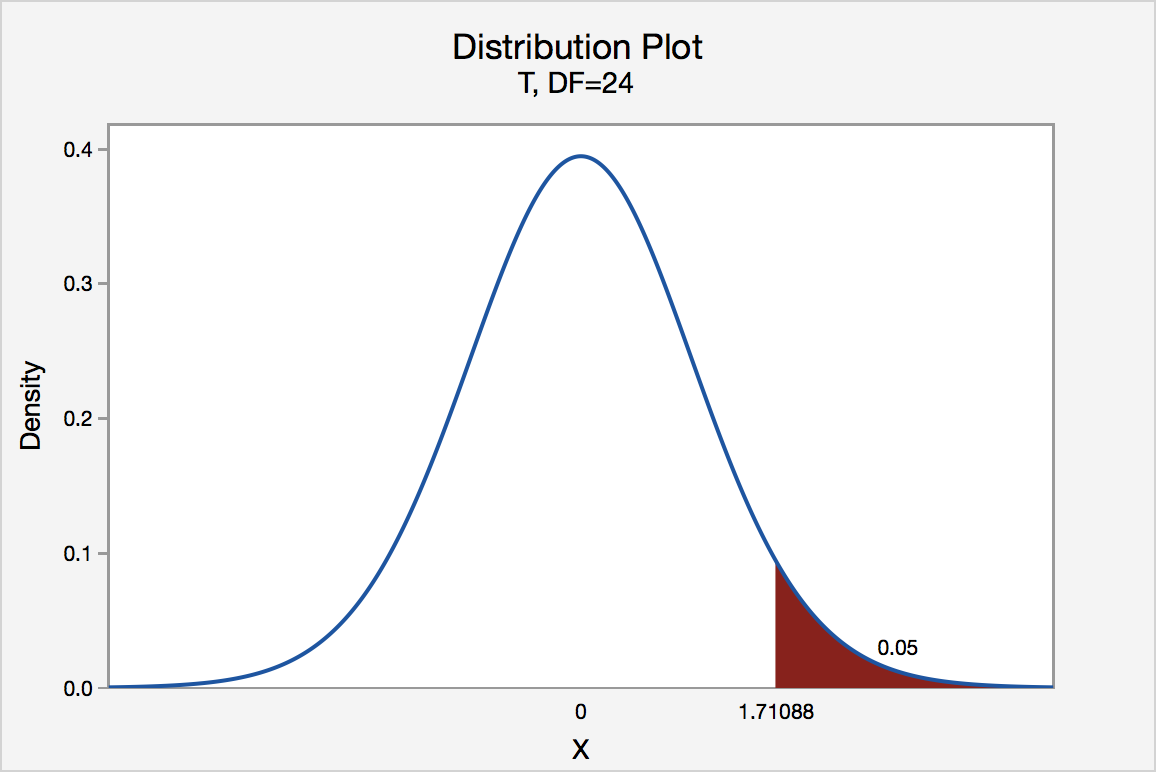
Since the engineer's test statistic, t* = 1.22, is not greater than 1.7109, the engineer fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.
If the engineer used the P-value approach to conduct his hypothesis test, he would determine the area under a tn - 1 = t24 curve and to the right of the test statistic t* = 1.22:
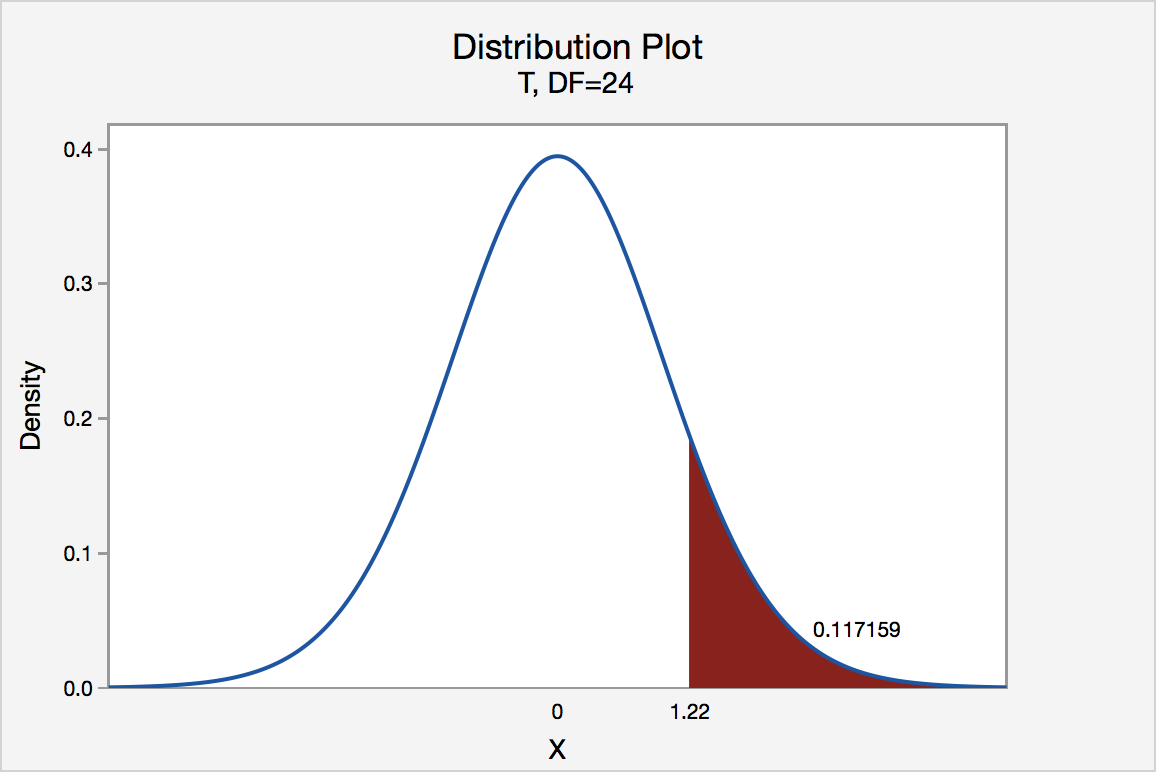
In the output above, Minitab reports that the P-value is 0.117. Since the P-value, 0.117, is greater than \(\alpha\) = 0.05, the engineer fails to reject the null hypothesis. There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.
Note that the engineer obtains the same scientific conclusion regardless of the approach used. This will always be the case.
Height of Sunflowers
A biologist was interested in determining whether sunflower seedlings treated with an extract from Vinca minor roots resulted in a lower average height of sunflower seedlings than the standard height of 15.7 cm. The biologist treated a random sample of n = 33 seedlings with the extract and subsequently obtained the following heights:
| Heights of 33 Sunflower Seedlings | ||||||||
|---|---|---|---|---|---|---|---|---|
| 11.5 | 11.8 | 15.7 | 16.1 | 14.1 | 10.5 | 9.3 | 15.0 | 11.1 |
| 15.2 | 19.0 | 12.8 | 12.4 | 19.2 | 13.5 | 12.2 | 13.3 | |
| 16.5 | 13.5 | 14.4 | 16.7 | 10.9 | 13.0 | 10.3 | 15.8 | |
| 15.1 | 17.1 | 13.3 | 12.4 | 8.5 | 14.3 | 12.9 | 13.5 | |
The biologist's hypotheses are:
H0 : μ = 15.7
HA : μ < 15.7
The biologist entered her data into Minitab and requested that the "one-sample t-test" be conducted for the above hypotheses. She obtained the following output:
Descriptive Statistics
| N | Mean | StDev | SE Mean | 95% Upper Bound |
|---|---|---|---|---|
| 33 | 13.664 | 2.544 | 0.443 | 14.414 |
$\mu$: mean of Height
Test
Null hypothesis H₀: $\mu$ = 15.7
Alternative hypothesis H₁: $\mu$ < 15.7
| T-Value | P-Value |
|---|---|
| -4.60 | 0.000 |
The output tells us that the average height of the n = 33 sunflower seedlings was 13.664 with a standard deviation of 2.544. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 13.664 by the square root of n = 33, is 0.443). The test statistic t* is -4.60, and the P-value, 0.000, is to three decimal places.
Minitab Note. Minitab will always report P-values to only 3 decimal places. If Minitab reports the P-value as 0.000, it really means that the P-value is 0.000....something. Throughout this course (and your future research!), when you see that Minitab reports the P-value as 0.000, you should report the P-value as being "< 0.001."
If the biologist set her significance level \(\alpha\) at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t* were less than -1.6939 (determined using statistical software or a t-table):s-3-3
Since the biologist's test statistic, t* = -4.60, is less than -1.6939, the biologist rejects the null hypothesis. That is, the test statistic falls in the "critical region." There is sufficient evidence, at the α = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.
If the biologist used the P-value approach to conduct her hypothesis test, she would determine the area under a tn - 1 = t32 curve and to the left of the test statistic t* = -4.60:
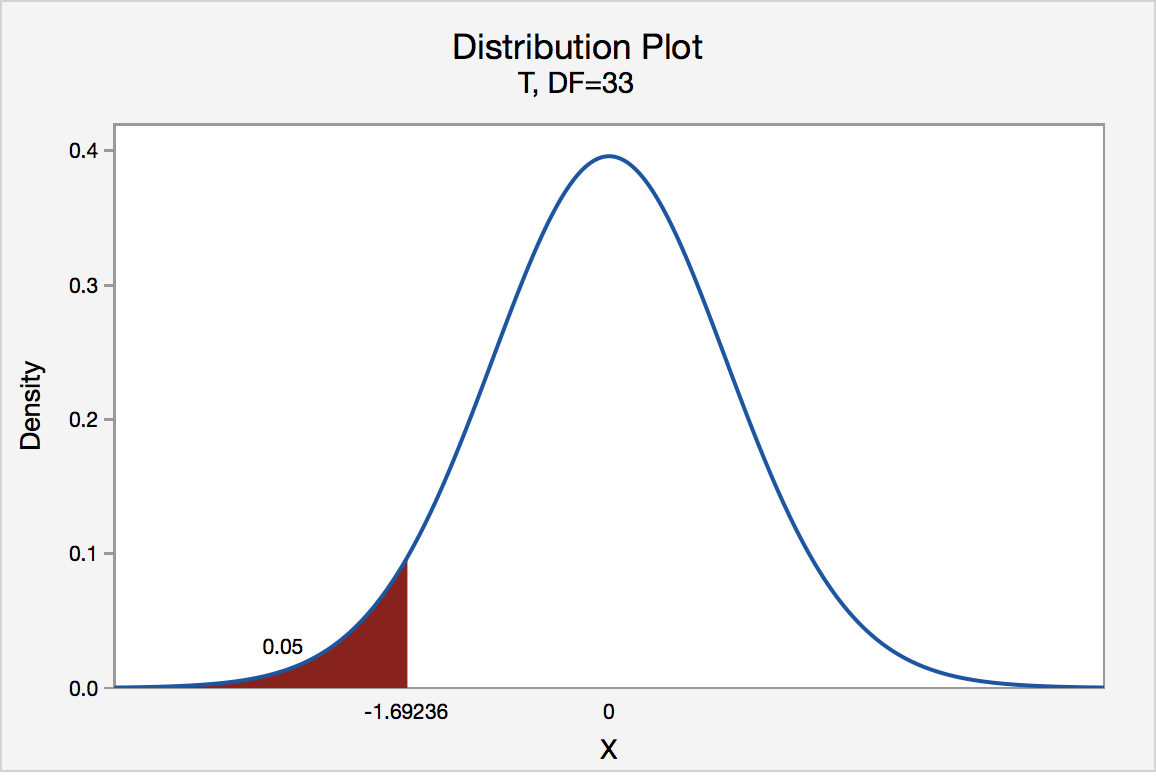
In the output above, Minitab reports that the P-value is 0.000, which we take to mean < 0.001. Since the P-value is less than 0.001, it is clearly less than \(\alpha\) = 0.05, and the biologist rejects the null hypothesis. There is sufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.
Note again that the biologist obtains the same scientific conclusion regardless of the approach used. This will always be the case.
Gum Thickness
A manufacturer claims that the thickness of the spearmint gum it produces is 7.5 one-hundredths of an inch. A quality control specialist regularly checks this claim. On one production run, he took a random sample of n = 10 pieces of gum and measured their thickness. He obtained:
| Thicknesses of 10 Pieces of Gum | ||||
|---|---|---|---|---|
| 7.65 | 7.60 | 7.65 | 7.70 | 7.55 |
| 7.55 | 7.40 | 7.40 | 7.50 | 7.50 |
The quality control specialist's hypotheses are:
H0 : μ = 7.5
HA : μ ≠ 7.5
The quality control specialist entered his data into Minitab and requested that the "one-sample t-test" be conducted for the above hypotheses. He obtained the following output:
Descriptive Statistics
| N | Mean | StDev | SE Mean | 95% CI for $\mu$ |
|---|---|---|---|---|
| 10 | 7.550 | 0.1027 | 0.0325 | (7.4765, 7.6235) |
$\mu$: mean of Thickness
Test
Null hypothesis H₀: $\mu$ = 7.5
Alternative hypothesis H₁: $\mu \ne$ 7.5
| T-Value | P-Value |
|---|---|
| 1.54 | 0.158 |
The output tells us that the average thickness of the n = 10 pieces of gums was 7.55 one-hundredths of an inch with a standard deviation of 0.1027. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 0.1027 by the square root of n = 10, is 0.0325). The test statistic t* is 1.54, and the P-value is 0.158.
If the quality control specialist sets his significance level \(\alpha\) at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t* were less than -2.2616 or greater than 2.2616 (determined using statistical software or a t-table):
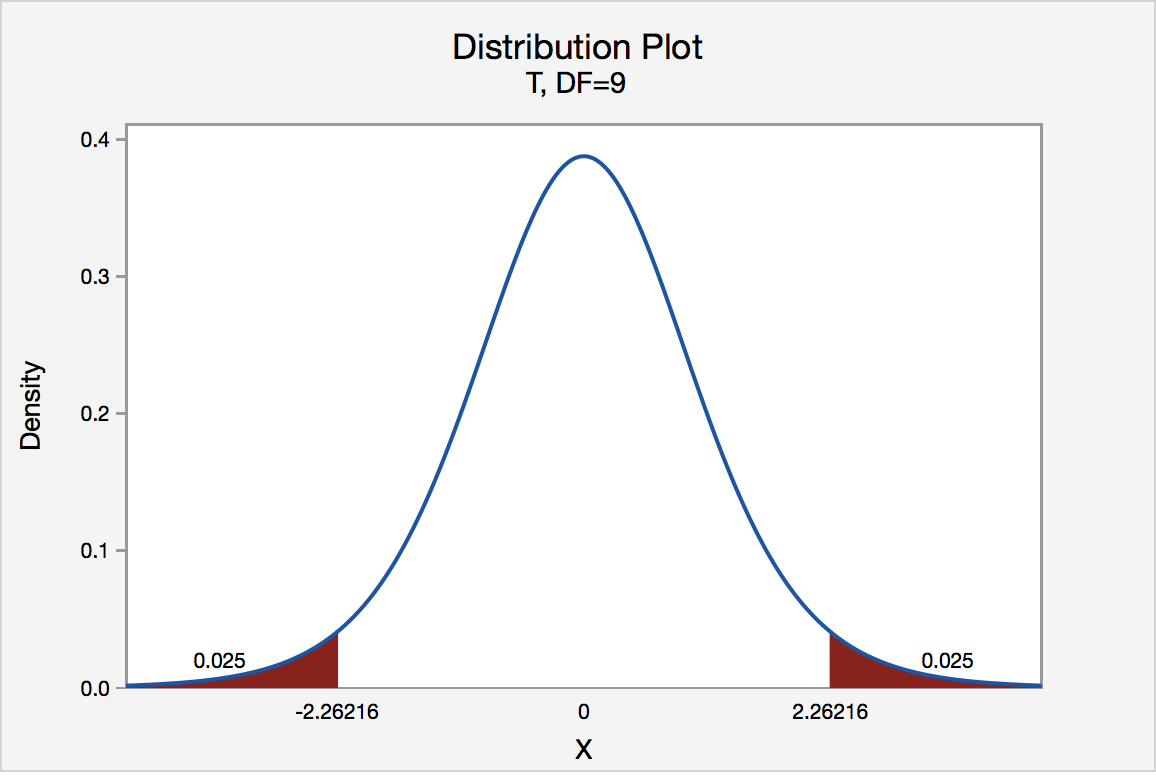
Since the quality control specialist's test statistic, t* = 1.54, is not less than -2.2616 nor greater than 2.2616, the quality control specialist fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean thickness of all of the manufacturer's spearmint gum differs from 7.5 one-hundredths of an inch.
If the quality control specialist used the P-value approach to conduct his hypothesis test, he would determine the area under a tn - 1 = t9 curve, to the right of 1.54 and to the left of -1.54:
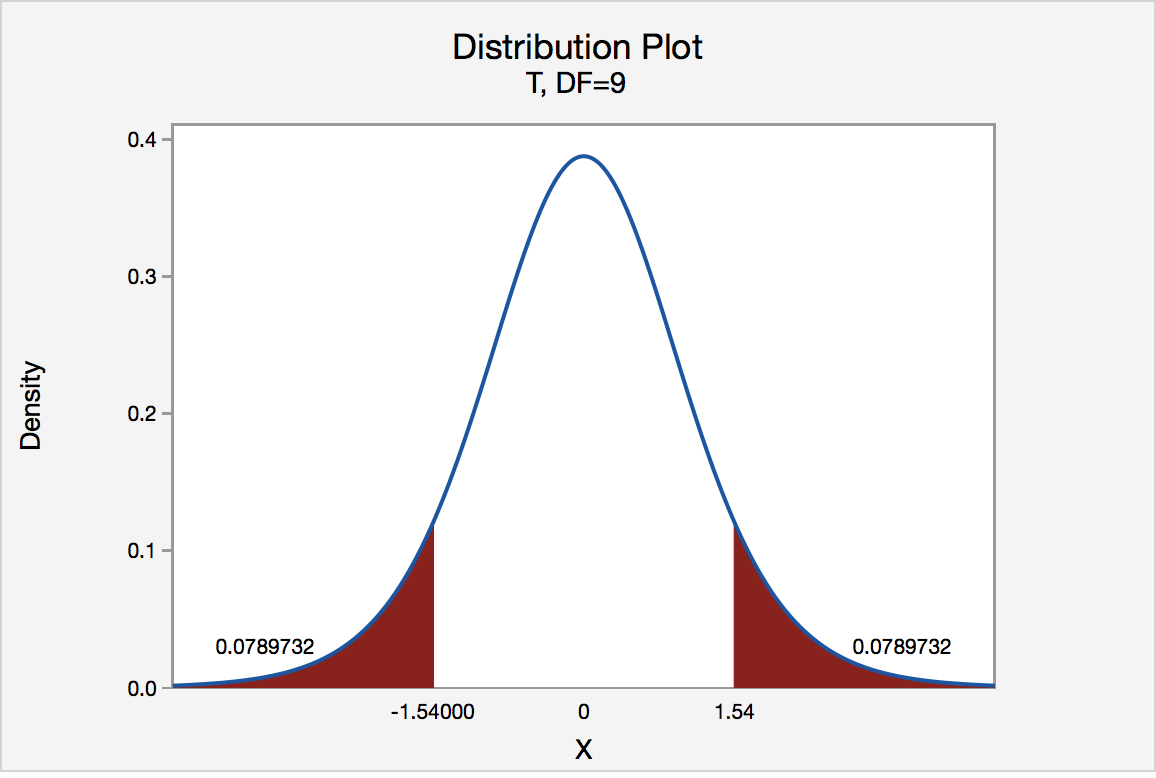
In the output above, Minitab reports that the P-value is 0.158. Since the P-value, 0.158, is greater than \(\alpha\) = 0.05, the quality control specialist fails to reject the null hypothesis. There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean thickness of all pieces of spearmint gum differs from 7.5 one-hundredths of an inch.
Note that the quality control specialist obtains the same scientific conclusion regardless of the approach used. This will always be the case.
In closing
In our review of hypothesis tests, we have focused on just one particular hypothesis test, namely that concerning the population mean \(\mu\). The important thing to recognize is that the topics discussed here — the general idea of hypothesis tests, errors in hypothesis testing, the critical value approach, and the P-value approach — generally extend to all of the hypothesis tests you will encounter.
S.4 Chi-Square Tests
S.4 Chi-Square TestsChi-Square Test of Independence
Do you remember how to test the independence of two categorical variables? This test is performed by using a Chi-square test of independence.
Recall that we can summarize two categorical variables within a two-way table, also called an r × c contingency table, where r = number of rows, c = number of columns. Our question of interest is “Are the two variables independent?” This question is set up using the following hypothesis statements:
- Null Hypothesis
- The two categorical variables are independent
- Alternative Hypothesis
- The two categorical variables are dependent
- Chi-Square Test Statistic
- \(\chi^2=\sum(O-E)^2/E\)
- where O represents the observed frequency. E is the expected frequency under the null hypothesis and computed by:
\[E=\frac{\text{row total}\times\text{column total}}{\text{sample size}}\]
We will compare the value of the test statistic to the critical value of \(\chi_{\alpha}^2\) with the degree of freedom = (r - 1) (c - 1), and reject the null hypothesis if \(\chi^2 \gt \chi_{\alpha}^2\).
Example S.4.1
Is gender independent of education level? A random sample of 395 people was surveyed and each person was asked to report the highest education level they obtained. The data that resulted from the survey are summarized in the following table:
| High School | Bachelors | Masters | Ph.d. | Total | |
|---|---|---|---|---|---|
| Female | 60 | 54 | 46 | 41 | 201 |
| Male | 40 | 44 | 53 | 57 | 194 |
| Total | 100 | 98 | 99 | 98 | 395 |
Question: Are gender and education level dependent at a 5% level of significance? In other words, given the data collected above, is there a relationship between the gender of an individual and the level of education that they have obtained?
Here's the table of expected counts:
| High School | Bachelors | Masters | Ph.d. | Total | |
|---|---|---|---|---|---|
| Female | 50.886 | 49.868 | 50.377 | 49.868 | 201 |
| Male | 49.114 | 48.132 | 48.623 | 48.132 | 194 |
| Total | 100 | 98 | 99 | 98 | 395 |
So, working this out, \(\chi^2= \dfrac{(60−50.886)^2}{50.886} + \cdots + \dfrac{(57 − 48.132)^2}{48.132} = 8.006\)
The critical value of \(\chi^2\) with 3 degrees of freedom is 7.815. Since 8.006 > 7.815, we reject the null hypothesis and conclude that the education level depends on gender at a 5% level of significance.
S.5 Power Analysis
S.5 Power AnalysisWhy is Power Analysis Important?
Consider a research experiment where the p-value computed from the data was 0.12. As a result, one would fail to reject the null hypothesis because this p-value is larger than \(\alpha\) = 0.05. However, there still exist two possible cases for which we failed to reject the null hypothesis:
- the null hypothesis is a reasonable conclusion,
- the sample size is not large enough to either accept or reject the null hypothesis, i.e., additional samples might provide additional evidence.
Power analysis is the procedure that researchers can use to determine if the test contains enough power to make a reasonable conclusion. From another perspective power analysis can also be used to calculate the number of samples required to achieve a specified level of power.
Example S.5.1
Let's take a look at an example that illustrates how to compute the power of the test.
Example
Let X denote the height of randomly selected Penn State students. Assume that X is normally distributed with unknown mean \(\mu\) and a standard deviation of 9. Take a random sample of n = 25 students, so that, after setting the probability of committing a Type I error at \(\alpha = 0.05\), we can test the null hypothesis \(H_0: \mu = 170\) against the alternative hypothesis that \(H_A: \mu > 170\).
What is the power of the hypothesis test if the true population mean were \(\mu = 175\)?
\[\begin{align}z&=\frac{\bar{x}-\mu}{\sigma / \sqrt{n}} \\
\bar{x}&= \mu + z \left(\frac{\sigma}{\sqrt{n}}\right) \\
\bar{x}&=170+1.645\left(\frac{9}{\sqrt{25}}\right) \\
&=172.961\\
\end{align}\]
So we should reject the null hypothesis when the observed sample mean is 172.961 or greater:
We get
\[\begin{align}\text{Power}&=P(\bar{x} \ge 172.961 \text{ when } \mu =175)\\
&=P\left(z \ge \frac{172.961-175}{9/\sqrt{25}} \right)\\
&=P(z \ge -1.133)\\
&= 0.8713\\
\end{align}\]
and illustrated below:
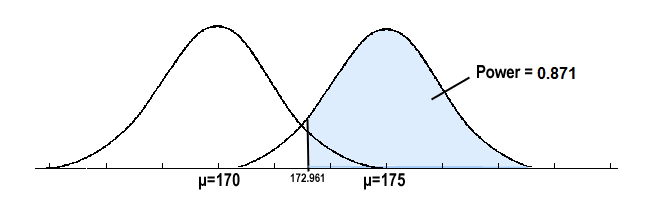
In summary, we have determined that we have an 87.13% chance of rejecting the null hypothesis \(H_0: \mu = 170\) in favor of the alternative hypothesis \(H_A: \mu > 170\) if the true unknown population mean is, in reality, \(\mu = 175\).
Calculating Sample Size
If the sample size is fixed, then decreasing Type I error \(\alpha\) will increase Type II error \(\beta\). If one wants both to decrease, then one has to increase the sample size.
To calculate the smallest sample size needed for specified \(\alpha\), \(\beta\), \(\mu_a\), then (\(\mu_a\) is the likely value of \(\mu\) at which you want to evaluate the power.
- Sample Size for One-Tailed Test
- \(n = \dfrac{\sigma^2(Z_{\alpha}+Z_{\beta})^2}{(\mu_0−\mu_a)^2}\)
- Sample Size for Two-Tailed Test
- \(n = \dfrac{\sigma^2(Z_{\alpha/2}+Z_{\beta})^2}{(\mu_0−\mu_a)^2}\)
Let's investigate by returning to our previous example.
Example S.5.2
Let X denote the height of randomly selected Penn State students. Assume that X is normally distributed with unknown mean \(\mu\) and standard deviation 9. We are interested in testing at \(\alpha = 0.05\) level , the null hypothesis \(H_0: \mu = 170\) against the alternative hypothesis that \(H_A: \mu > 170\).
Find the sample size n that is necessary to achieve 0.90 power at the alternative μ = 175.
\[\begin{align}n&= \dfrac{\sigma^2(Z_{\alpha}+Z_{\beta})^2}{(\mu_0−\mu_a)^2}\\ &=\dfrac{9^2 (1.645 + 1.28)^2}{(170-175)^2}\\ &=27.72\\ n&=28\\ \end{align}\]
In summary, you should see how power analysis is very important so that we are able to make the correct decision when the data indicate that one cannot reject the null hypothesis. You should also see how power analysis can also be used to calculate the minimum sample size required to detect a difference that meets the needs of your research.
S.6 Test of Proportion
S.6 Test of ProportionLet us consider the parameter p of the population proportion. For instance, we might want to know the proportion of males within a total population of adults when we conduct a survey. A test of proportion will assess whether or not a sample from a population represents the true proportion of the entire population.
Critical Value Approach
The steps to perform a test of proportion using the critical value approval are as follows:
- State the null hypothesis H0 and the alternative hypothesis HA.
- Calculate the test statistic:
\[z=\frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}\]
where \(p_0\) is the null hypothesized proportion i.e., when \(H_0: p=p_0\)
-
Determine the critical region.
-
Make a decision. Determine if the test statistic falls in the critical region. If it does, reject the null hypothesis. If it does not, do not reject the null hypothesis.
Example S.6.1
Newborn babies are more likely to be boys than girls. A random sample found 13,173 boys were born among 25,468 newborn children. The sample proportion of boys was 0.5172. Is this sample evidence that the birth of boys is more common than the birth of girls in the entire population?
Here, we want to test
\(H_0: p=0.5\)
\(H_A: p>0.5\)
The test statistic
\[\begin{align} z &=\frac{\hat{p}-p_o}{\sqrt{\frac{p_0(1-p_0)}{n}}}\\
&=\frac{0.5172-0.5}{\sqrt{\frac{0.5(1-0.5)}{25468}}}\\
&= 5.49 \end{align}\]
We will reject the null hypothesis \(H_0: p = 0.5\) if \(\hat{p} > 0.5052\) or equivalently if Z > 1.645
Here's a picture of such a "critical region" (or "rejection region"):
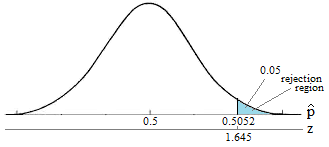
It looks like we should reject the null hypothesis because:
\[\hat{p}= 0.5172 > 0.5052\]
or equivalently since our test statistic Z = 5.49 is greater than 1.645.
Our Conclusion: We say there is sufficient evidence to conclude boys are more common than girls in the entire population.
\(p\)- value Approach
Next, let's state the procedure in terms of performing a proportion test using the p-value approach. The basic procedure is:
- State the null hypothesis H0 and the alternative hypothesis HA.
- Set the level of significance \(\alpha\).
- Calculate the test statistic:
\[z=\frac{\hat{p}-p_o}{\sqrt{\frac{p_0(1-p_0)}{n}}}\]
-
Calculate the p-value.
-
Make a decision. Check whether to reject the null hypothesis by comparing the p-value to \(\alpha\). If the p-value < \(\alpha\) then reject \(H_0\); otherwise do not reject \(H_0\).
Example S.6.2
Let's investigate by returning to our previous example. Again, we want to test
\(H_0: p=0.5\)
\(H_A: p>0.5\)
The test statistic
\[\begin{align} z &=\frac{\hat{p}-p_o}{\sqrt{\frac{p_0(1-p_0)}{n}}}\\
&=\frac{0.5172-0.5}{\sqrt{\frac{0.5(1-0.5)}{25468}}}\\
&= 5.49 \end{align}\]
The p-value is represented in the graph below:
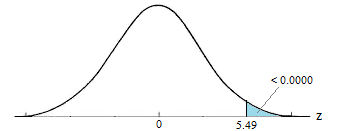
\[P = P(Z \ge 5.49) = 0.0000 \cdots \doteq 0\]
Our Conclusion: Because the p-value is smaller than the significance level \(\alpha = 0.05\), we can reject the null hypothesis. Again, we would say that there is sufficient evidence to conclude boys are more common than girls in the entire population at the \(\alpha = 0.05\) level.
As should always be the case, the two approaches, the critical value approach and the p-value approach lead to the same conclusion.
S.7 Self-Assess
S.7 Self-AssessWe suggest you...
- Review the concepts and methods on the pages in this section of this website.
- Download and Complete the Self-Assessment Exam.
- Determine your Score by reviewing the Self-Assessment Exam Solutions
A score below 70% suggests that the concepts and procedures that are covered in STAT 500 have not been mastered adequately. Students are strongly encouraged to take STAT 500, thoroughly review the materials that are covered in the sections above or take additional coursework that focuses on these foundations.
If you have struggled with the concepts and methods that are presented here, you will indeed struggle in any of the graduate-level courses included in the Master of Applied Statistics program above STAT 500 that expect and build on this foundation.
Note: These materials are NOT intended to be a complete treatment of the ideas and methods used in basic statistics. These materials and the accompanying self-assessment are simply intended as simply an 'early warning signal' for students. Also, please note that completing the self-assessment successfully does not automatically ensure success in any of the courses that use this foundation.
Calculus Review
Calculus ReviewSTAT 414 and STAT 415 are both required courses that were designed for the Master of Applied Statistics degree. These two courses provide the theoretical and mathematical foundations for the degree. Most students find these courses to be very challenging. The regularity of work and the rigorous nature of the concepts and methods can be daunting. For this reason, it is imperative that you have a working knowledge of multidimensional calculus as a prerequisite.
Many of our returning, working professional students report that they had taken the standard three-course calculus sequence (for example, MATH 140, MATH 141, and MATH 230) but these courses were completed a number of years ago. While it is relevant that you recognize these techniques it is expected that you can implement them.
An easy way to think about this may be in terms of an analogy. Perhaps as a child growing up you learned to play a musical instrument, and you might have been quite good. However, life has other plans for you and you realize that you have not picked up that instrument, or sat down at a piano for quite some time. While you might recognize the notes, the scales, or the keys to use, playing a song is not 'at your fingertips' as it once may have been. Students taking STAT 414 need to be ready to 'play the songs'! Re-learning the notes, the scales, and the keys at the same time as you are learning new concepts that involve these skills is often too much to handle and you get behind, and getting behind is no fun at all.
The review materials below are intended to provide a simple review of the calculus techniques most frequently used in the course. These are the topics that we want you to make sure that you have working knowledge of before you take STAT 414. They include:
- differentiation,
- integration,
- series,
- limits, and
- multivariate calculus.
We want our students to be successful! And we know that students that do not possess a working knowledge of these topics will struggle to participate successfully in STAT 414.
Review Materials
Are you ready? As a means of helping students assess whether or not what they currently know and can do will meet the expectations of instructors of STAT 414, the online program has put together a brief review of these concepts and methods. Each of these sections includes short self-assessment questions that will help you determine if this prerequisite knowledge is readily available for you to apply.
If you have struggled with the concepts and methods that are presented here, you will no doubt struggle in STAT 414 because this course expects and works off of this foundation.
Please Note: These materials are NOT intended to be a complete treatment of the ideas and methods used in multidimensional calculus. These materials and the self-assessment are simply intended as simply an 'early warning signal' for students. Also, please note that completing the self-assessment successfully does not automatically ensure success in any of the courses that use these foundation materials. Please keep in mind that this is a review only. It is not an exhaustive list of the material you need to have learned in your previous math classes. This review is meant only to be a simple guide of things you should remember.
C.1 Summations and Series
C.1 Summations and SeriesSummations and Series are an important part of discrete probability theory. We provide a brief review of some of the series used in STAT 414. While it is important to recall these special series, you should also take the time to practice. For a more in-depth review, there are links to Khan Academy.
Summations
First, it is important to review the notation. The symbol, \(\sum\), is a summation. Suppose we have the sequence, \(a_1, a_2, \cdots, a_n\), denoted \(\{a_n\}\), and we want to sum all their values. This can be written as
\[\sum_{i=1}^n a_i\]
Here are some special sums:
- \(\sum_{i=1}^n i=1+2+\cdots+n=\frac{n(n+1)}{2}\)
- \(\sum_{i=1}^n i^2=1^2+2^2+\cdots+n^2=\frac{n(n+1)(2n+1)}{6}\)
- The Binomial Theorem:
It is possible to expand any power of \(x+y\) to the sum
\[(x+y)^n=\sum_{i=0}^n {n \choose i} x^{n-i}y^i\]
where
\[{n\choose i}=\frac{n(n-1)(n-2)\cdots(n-i-1)}{i!}=\frac{n!}{(n-i)!i!}\]
Examples using the Binomial Theorem Video, (Khan Academy).
Series
When n is a finite number, the value of the sum can be easily determined. How do we find the sum when the sequence is infinite? For example, suppose we have an infinite sequence, \(a_1, a_2, \cdots\). The infinite series is denoted:
\[S=\sum_{i=1}^\infty a_i\]
For infinite series, we consider the partial sums. Some partial sums are
\[\begin{align*}
& S_1=\sum_{i=1}^1 a_i=a_1 \\
& S_2=\sum_{i=1}^2 a_i=a_1+a_2 \\
& S_3=\sum_{i=1}^3 a_i=a_1+a_2+a_3\\
& \vdots\\
& S_n=\sum_{i=1}^n a_i=a_1+a_2+\cdots+a_n
\end{align*}\]
An infinite series converges and has sum S if the sequence of partial sums, \(\{S_n\}\) converges to S. Thus, if
\[S=\lim_{n\rightarrow \infty} \{S_n\}\]
then the series converges to S. If \(\{S_n\}\) diverges, then the series diverges.
Review Convergence and Divergence of Series Video, (Khan Academy).
These are some of the special series used in STAT 414. It would be helpful to review more than what is listed below.
Geometric series
A geometric series has the form
\[S=\sum_{k=1}^\infty a r^{k-1}=a+ar+ar^2+ar^3+\cdots\]
where \(a\neq 0\). A geometric series converges to \(\frac{a}{1-r}\) if \(|r|<1\), but diverges if \(|r|\ge1\).
More examples and Explanation of the Geometric Series Video, (Khan Academy).
A special case of the geometric series
\[\frac{1}{1-x}=1+x+x^2+x^3+\cdots\]
for $-1<x<1$.
The Taylor (or Maclaurin) series of \(e^x\):
The series:
\[\sum_{i=0}^\infty \frac{x^i}{i!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots\]
for \(-1\le x\le 1\) converges to \(e^x\).
Review for the Taylor (or Maclaurin) Series Video, (Khan Academy).
Example C.1
\[S=\frac{1}{3}-\frac{1}{6}+\frac{1}{12}-\frac{1}{24}+\cdots=\sum_{x=0}^{\infty} \frac{1}{3(-2)^x}\]
This is a geometric series with \(a=\frac{1}{3}\) and \(r=-\frac{1}{2}\). Therefore, it converges to
\[\frac{a}{1-r}=\frac{\frac{1}{3}}{1+\frac{1}{2}}=\frac{2}{9}\]
C.2 Derivatives
C.2 DerivativesA complete review of derivatives would be lengthy. We try to touch on some topics that are used often in STAT 414 but not everything can be covered in the review. There are many good calculus books and websites to help you review. Students like the book Forgotten Calculus: A Refresher Course with Applications to Economics and Business by Barbara Lee Bleau, Ph.D. as a reference.
The definition of a derivative is
\[f^\prime(x)=\frac{d}{dx} f(x)=\lim_{h\rightarrow 0} \frac{f(x+h)-f(x)}{h}\]
The derivative is the slope of the tangent line to the graph of \(f(x)\), assuming the tangent line exists. You can find further explanations of derivatives on the web using websites like Khan Academy. Below are rules for determining derivatives and links for extra help.
- Common Derivatives and Rules
- Power Rule:
\(\frac{d}{dx}x^n=nx^{n-1}\) (Power Rule, Khan Academy) - \(\frac{d}{dx} \ln x=\frac{1}{x}\)
- \(\frac{d}{dx} a^x=a^x\ln a\)
- \(\frac{d}{dx} e^x=e^x\)
- Power Rule:
- Product rule
\(\begin{equation}\left[f(x)g(x)\right]^\prime=f^\prime(x)g(x)+f(x)g^\prime(x)\end{equation}\) (Product Rule, Khan Academy) - Quotient rule
\(\begin{equation} \left[\frac{f(x)}{g(x)}\right]^\prime=\frac{g(x)f^\prime(x)-f(x)g^\prime(x)}{\left(g(x)\right)^2}\end{equation}\) (Quotient Rule, Khan Academy) - Chain Rule
Let \(y=f(g(x))\) where f and g are functions, g is differentiable at x, and f is differentiable at \(g(x)\). Then the derivative of y is \(f^\prime(g(x))g^\prime(x)\). (Chain Rule, Khan Academy) - L'Hopital's Rule
- For the type \(0/0\): Suppose that \(\lim_{x\rightarrow u} f(x)=0\) and \(\lim_{x\rightarrow u} g(x)=0\). If \(\lim_{x\rightarrow u}\left[\frac{f^\prime(x)}{g^\prime(x)}\right]\) exists in either the finite or infinite sense, then\[\begin{equation}\lim_{x\rightarrow u} \frac{f(x)}{g(x)}=\lim_{x\rightarrow u} \frac{f^\prime(x)}{g^\prime(x)}=\frac{\lim_{x\rightarrow u} f^\prime(x)}{\lim_{x\rightarrow u} g^\prime(x)}\end{equation}\]
- For the type \(\infty/\infty\): Suppose that \(\lim_{x\rightarrow u} |f(x)|=\infty\) and \(\lim_{x\rightarrow u} |g(x)|=\infty\). If \(\lim_{x\rightarrow u}\left[\frac{f^\prime(x)}{g^\prime(x)}\right]\) exists in either the finite or infinite sense, then\[\begin{equation}\lim_{x\rightarrow u} \frac{f(x)}{g(x)}=\lim_{x\rightarrow u} \frac{f^\prime(x)}{g^\prime(x)}=\frac{\lim_{x\rightarrow u} f^\prime(x)}{\lim_{x\rightarrow u} g^\prime(x)}\end{equation}\]
- Other indeterminate forms can also be solved using L'Hopital's Rule, such as \(0^0\) and \(\infty^0\). It would be a good idea for review the uses of L'Hopital's Rule. (L'Hopital's Rule, Khan Academy)
Example C.2.1
Find the derivative of \(f(x)\) for the following:
- \(f(x)=10x^9-5x^5+7x^3-9\)
- \(f(x)=\dfrac{x}{x^2+5}\)
- \(f(x)=\dfrac{1}{\sqrt{x}}\)
- \(f^\prime(x)=90x^8-25x^4+21x^2\)
- Using the Quotient Rule, \(f^\prime(x)=\dfrac{x^2+5-x(2x)}{(x^2+5)^2}=\dfrac{-x^2+5}{(x^2+5)^2}\)
- Using the Power Rule, \(f^\prime(x)=-\dfrac{1}{2x\sqrt{x}}\)
Example C.2.2
C.3 Integrals
C.3 IntegralsAs with the review of Derivatives, it would be challenging to include a full review of Integrals. In this review, we try to include the most common integrals and rules used in STAT 414. There are many helpful websites and texts out there to help you review. We have provided links to Khan Academy for you to take a look at if you have difficulty recalling these methods.
For a function, \(f(x)\), its indefinite integral is:
\[\int f(x)\; dx=F(x)+C, \qquad \text{where } F^\prime(x)=f(x)\]
We provide a short list of common integrals and rules that are used in STAT 414. It is important to have a lot of practice and keep these skills fresh.
Common Integrals and Rules
- \(\int_a^a f(x)dx=0\)
- \(\int_a^b f(x)d(x)=-\int_b^a f(x)d(x)\)
- \(\int x^rdx=\frac{x^{r+1}}{r+1}+C\)
The Fundamental Theorem of Calculus:
Let \(f\) be integrable on \([a,b]\) and let \(F\) be any antiderivative of \(f\) there. Then, \(\int_a^b f(x)d(x)=F(b)-F(a)\). (FTC, Khan Academy)
- \(\int x^n dx=\dfrac{1}{n+1}x^{n+1}+C, \;\;n\neq(-1)\)
- \(\int \dfrac{1}{x}dx=\ln |x| +C\)
- \(\int e^x dx=e^x +C\)
Integration Using Substitution:
Let \(g\) have a continuous derivative on \([a,b]\) and let \(f\) be continuous on the range of \(g\). Then
\[\begin{equation}
\int_a^b f\left(g(x)\right)g^\prime(x)dx=\int_{g(a)}^{g(b)}f(u)du
\end{equation}\]
where \(u=g(x)\). (u-Substitution, Khan Academy)
Integration by Parts
\[\begin{equation}
\int_a^b udv=\left[uv\right]_a^b-\int_a^b vdu \end{equation}\].
(Integration by Parts, Khan Academy)
Example C.3.1
Integrate the following function from 0 to $t$
\[f(x)=\dfrac{2}{1000^2}xe^{-(x/1000)^2}\]
\[\int_0^t \frac{2}{1000^2}xe^{-(x/1000)^2} dx\label{eqn1}\]
Let \(u=\left(\frac{x}{1000}\right)^2\). Then \(du=\frac{2}{1000^2}xdx\). The equation becomes...
\[\begin{align*}
&= \int_0^{\left(\frac{t}{1000}\right)^2} e^{-u}du =-e^{-u}|_{0}^{\left(\frac{t}{1000}\right)^2}\\
&= -e^{-\left(\frac{t}{1000}\right)^2}-(-1)=1-e^{-\left(\frac{t}{1000}\right)^2}.
\end{align*}\]
Example C.3.2
Integrate the following:
\[\int_0^5 x^2e^{-x}dx\]
Let us begin by setting up integration by parts. Let
\[\begin{align*}
& u=x^2 \qquad dv=e^{-x}dx\\
& du=2xdx \qquad v=-e^{-x}
\end{align*}\]
Then
\[\begin{align*}
uv|_0^5-\int_0^5 vdu &=-x^2e^{-x}|_0^5+2\int_0^5xe^{-x}dx\\
&= -x^2e^{-x}|_0^5+2\left[-xe^{-x}|_0^5+\int_0^5 e^{-x}dx\right]\\
&= -x^2e^{-x}|_0^5+2\left[-xe^{-x}|_0^5-e^{-x}|_0^5\right]\approx 1.75
\end{align*}\]
Example C.3.3
Integrate the following from \(-\infty\) to \(\infty\).
\[f(y)=\frac{1}{2}e^{-|y|+ty}, \;\; \text{ for } -\infty<y<\infty\]
\begin{align*}
\int_{-\infty}^{\infty} \frac{1}{2} e^{ty-|y|}dy &= \int_{-\infty}^0 \frac{1}{2}e^{y+ty}dy+\int_0^{\infty} \frac{1}{2}e^{-y+ty}dy\\
& = \int_{-\infty}^0 \frac{1}{2}e^{y(1+t)}dy+\int_0^{\infty} \frac{1}{2}e^{-y(1-t)}dy\\
& = \frac{1}{2(1+t)}+ \frac{1}{2(1-t)}=\frac{1}{2}\left(\frac{1-t+t+1}{(1+t)(1-t)}\right)\\
& =\frac{1}{(1-t)(1+t)}
\end{align*}
C.4 Multivariable Calculus
C.4 Multivariable CalculusIn this review, we present a couple of the more important Multivariable Calculus methods commonly used in STAT 414, mainly for Exam 4 and the Final Exam. While this is not a complete review, you should use this to refresh your memory and guide you to where you need to spend time reviewing. As always, practice is key!
First, multivariable calculus involves functions of several variables. For simplicity, we focus on the functions of two variables. You can find information on the web or in other texts to review in more detail if you need.
Partial Derivatives
Let's begin with Partial Derivatives. Suppose we have the function \(f(x,y)\). The partial derivative with respect to x would be
\[f_x(x,y)=\lim_{h\rightarrow 0} \frac{f(x-h, y)}{x-h}\]
Similarly, the partial derivative of \(f(x,y)\) with respect to \(y\) would be
\[f_y(x,y)=\lim_{h\rightarrow 0} \frac{f(x, y-h)}{y-h}\]
The notation for partial derivatives is not the same for all texts. You should be able to recognize the different forms. The notation, for example, for the partial derivative of $f(x,y)$, with respect to $x$, could be denoted as:
\[f_x(x,y)=\frac{\partial}{\partial x}f(x, y)=\frac{\partial f}{\partial x}\]
Derivatives of Multivariable Functions Video, (Khan Academy)
Double Integrals
Integrating over regions will be important in STAT 414. Suppose we have the function \(f(x,y)\), the over the region R, would be:
\[\int \int_R f(x,y)\; dx dy\]
Consider the rectangular region defined by \(a\le x\le b\) and \(c\le y\le d\), or \(R=[a,b]\times[c, d]\). Then the iterated integral would be:
\( \int_c^d \left[\int_a^b f(x,y) dx\right] dy=\int_a^b \left[\int_c^d f(x,y) dy\right] dx \)
When the region is not rectangular, things can get complicated. It is important to draw out the support space and consider the region when building these double integrals.
Double Integrals Video, (Khan Academy)
Example C.4.1
First, let's find the partial of x. To do this, we consider y as a constant.
\[\dfrac{\partial f}{\partial x}=-\dfrac{2}{x^3}-y\]
Now, let's find \(\dfrac{\partial f}{\partial y}\).
\[\dfrac{\partial f}{\partial y}=\dfrac{3}{\sqrt{y}}-x\]
Example C.4.2
Integrate \(f(x,y) =24xy\). For \(0< x < 1, 0 <y<1\) and \(x+y < 1\) over the space where \(x+y<\dfrac{1}{2}\).
\begin{align*}
\int_0^{1/2}\int_{0}^{1/2-y} 24xy\; dx \; dy &=\int_0^{1/2} 12y^3-12y^2+3y\; dy\\
& = 3y^4-4y^3+\dfrac{3}{2}y^2|_0^{1/2}\\&=3\left(\dfrac{1}{2}\right)^4-4\left(\dfrac{1}{2}\right)^3+\dfrac{3}{2}\left(\dfrac{1}{2}\right)^2\\
& = \dfrac{1}{16}
\end{align*}
Matrix Algebra Review
Matrix Algebra ReviewMatrix Algebra: A Review
The Prerequisites Checklist page on the Department of Statistics website lists a number of courses that require a working knowledge of Matrix algebra as a prerequisite. Students who do not have this foundation or have not reviewed this material within the past couple of years will struggle with the concepts and methods that build on this foundation. The courses that require this foundation include:
- STAT 414 - Introduction to Probability Theory
- STAT 501 - Regression Methods
- STAT 504 - Analysis of Discrete Data
- STAT 505 - Applied Multivariate Statistical Analysis
Review Materials
Many of our returning, working professional students report that they had taken courses that included matrix algebra topics but often these courses were taken a number of years ago. As a means of helping students assess whether or not what they currently know and can do will meet the expectations of instructors in the courses above, the online program has put together a brief review of these concepts and methods. This is then followed by a short self-assessment exam that will help give you an idea if you still have the necessary background.
Self-Assessment Procedure
- Review the concepts and methods on the pages in this section of this website. Note the courses that certain sections are aligned with as prerequisites:
STAT 414 STAT 501 STAT 504 STAT 505 M.1 - Matrix Definitions Required Required Required Required M.2 - Matrix Arithmetic Required Required Required Required M.3 - Matrix Properties Required Required Required Required M.4 - Matrix Inverse Required Required Required Required M.5 - Advanced Topics Recommended Recommended Recommended 5.1, 5.4, Required
5.2, 5.3, Recommended - Download and complete the Self-Assessment Exam
- Review the Self-Assessment Exam Solutions and determine your score.
Students who score below 70% (fewer than 21 questions correct) should consider further review of these materials and are strongly encouraged to take a course like MATH 220 or an equivalent course at a local college or community college.
If you have struggled with the concepts and methods that are presented here, you will indeed struggle in the courses above that expect this foundation.
Please Note: These materials are NOT intended to be a complete treatment of the ideas and methods used in Matrix algebra. These materials and the self-assessment are simply intended as simply an 'early warning signal' for students. Also, please note that completing the self-assessment successfully does not automatically ensure success in any of the courses that use these foundation materials.
M.1 Matrix Definitions
M.1 Matrix Definitions- Matrix
-
A matrix is a rectangular collection of numbers. Generally, matrices are denoted as bold capital letters. For example:
\[A = \begin{pmatrix} 1 & -5 & 4\\
2 & 5 & 3 \end{pmatrix}\]
A is a matrix with two rows and three columns. For that reason, it is called a 2 by 3 matrix. This is called the dimension of a matrix.
- Dimension
-
The dimension of a matrix is expressed as number of rows × number of columns. So,
\[B = \begin{pmatrix} 1 & -5 & 4 \\ 5 & 3 & -8 \\ 1 & 5 & 4 \\ 2 & 5 & 3 \end{pmatrix}\]
B is a 4 × 3 matrix. It is common to refer to elements in a matrix by subscripts, like so.
\[B = \begin{pmatrix} b_{1,1} & b_{1,2} & b_{1,3}\\ b_{2,1} & b_{2,2} & b_{2,3}\\ b_{3,1} & b_{3,2} & b_{3,3}\\ b_{4,1} & b_{4,2} & b_{4,3} \end{pmatrix}\]
With the row first and the column second. So in this case, \(b_{2,1} = 5\) and \(b_{1,3} =4\).
- Vector
-
A vector is a matrix with only one row (called a row vector) or only one column (called a column vector). For example:
\[C = \begin{pmatrix} 2 & 7 & -3 & 5 \end{pmatrix}\]
C is a 4 dimensional row vector.
\[D = \begin{pmatrix} 2 \\9 \\-3 \\3\\ 6\\ \end{pmatrix}\]
D is a 5 dimensional column vector. An "ordinary" number can be thought of as a 1 × 1 matrix, also known as a scalar. Some examples of scalars are shown below:
\[ E = \pi \]
\[ F = 6 \]
M.2 Matrix Arithmetic
M.2 Matrix ArithmeticTranspose a Matrix
To take the transpose of a matrix, simply switch the rows and column of a matrix. The transpose of \(A\) can be denoted as \(A'\) or \(A^T\).
For example
\[A = \begin{pmatrix} 1 & -5 & 4 \\ 2 & 5 & 3 \end{pmatrix}\]
\[A' = A^T = \begin{pmatrix} 1 & 2\\ -5 & 5\\ 4 & 3 \end{pmatrix}\]
If a matrix is its own transpose, then that matrix is said to be symmetric. Symmetric matrices must be square matrices, with the same number of rows and columns.
One example of a symmetric matrix is shown below:
\[ A = \begin{pmatrix} 1 & -5 & 4 \\ -5 & 7 & 3\\ 4 & 3 & 3 \end{pmatrix} = A' = A^T \]
Matrix Addition
To perform matrix addition, two matrices must have the same dimensions. This means they must have the same number of rows and columns. In that case simply add each individual components, like below.
For example
\[A + B = \begin{pmatrix} 1 & -5 & 4 \\ 2 & 5 & 3 \end{pmatrix} + \begin{pmatrix} 8 & -3 & -4 \\ 4 & -2 & 9 \end{pmatrix} = \begin{pmatrix} 1 + 8 & -5 - 3 & 4 - 4 \\ 2 + 4 & 5 -2 & 3 + 9 \end{pmatrix} = \begin{pmatrix} 9 & -8 & 0\\ 6 & 3 & 12 \end{pmatrix}\]
Matrix addition does have many of the same properties as "normal" addition.
\[A + B = B + A\]
\[A + (B + C) = (A + B) + C\]
In addition, if one wishes to take the transpose of the sum of two matrices, then
\[A^T + B^T = (A+B)^T \]
Matrix Scalar Multiplication
To multiply a matrix by a scalar, also known as scalar multiplication, multiply every element in the matrix by the scalar.
For example...
\[ 6*A = 6 * \begin{pmatrix} 1 & -5 & 4\\ 2 & 5 & 3 \end{pmatrix} = \begin{pmatrix} 6 * 1 & 6 *-5 & 6 * 4\\ 6 * 2 & 6 *5 & 6 * 3 \end{pmatrix} = \begin{pmatrix} 6 & -30 & 24 \\ 12 & 30 & 18 \end{pmatrix}\]
To multiply two vectors with the same length together is to take the dot product, also called inner product. This is done by multiplying every entry in the two vectors together and then adding all the products up.
For example, for vectors x and y, the dot product is calculated below
\[ x \cdot y = \begin{pmatrix} 1 & -5 & 4 \end{pmatrix} * \begin{pmatrix} 4 & -2 & 5 \end{pmatrix} = 1*4 + (-5)*(-2) + 4*5 = 4+10+20 = 34\]
Matrix Multiplication
To perform matrix multiplication, the first matrix must have the same number of columns as the second matrix has rows. The number of rows of the resulting matrix equals the number of rows of the first matrix, and the number of columns of the resulting matrix equals the number of columns of the second matrix. So a 3 × 5 matrix could be multiplied by a 5 × 7 matrix, forming a 3 × 7 matrix, but one cannot multiply a 2 × 8 matrix with a 4 × 2 matrix. To find the entries in the resulting matrix, simply take the dot product of the corresponding row of the first matrix and the corresponding column of the second matrix.
For example
\[ C*D = \begin{pmatrix} 3 & -9 & -8\\ 2 & 4 & 3 \end{pmatrix} * \begin{pmatrix} 7 & -3\\ -2 & 3\\ 6 & 2 \end{pmatrix} \]
\[ C*D = \begin{pmatrix} 3*7 + (-9)*(-2) + (-8)*6 & 3*(-3) + (-9)*3 + (-8)*2 \\ 2*7 + 4*(-2) + 3*6 & 2*(-3) + 4*3 + 3*2 \end{pmatrix}\]
\[ C*D = \begin{pmatrix} 21 + 18 - 48 & - 9 - 27 - 16 \\14 - 8 + 18 & - 6 + 12 + 6 \end{pmatrix} = \begin{pmatrix} -9 & - 52\\ 24 & 12 \end{pmatrix} \]
Matrix multiplication has some of the same properties as "normal" multiplication , such as
\[ A(BC) = (AB)C\]
\[A(B + C) = AB + AC\]
\[(A + B)C = AC + BC\]
However matrix multiplication is not commutative. That is to say A*B does not necessarily equal B*A. In fact, B*A often has no meaning since the dimensions rarely match up. However, you can take the transpose of matrix multiplication. In that case \((AB)^T = B^T A^T\).
M.3 Matrix Properties
M.3 Matrix PropertiesIdentity Matrices
An identity matrix is a square matrix where every diagonal entry is 1 and all the other entries are 0. The following two matrices are identity matrices and diagonal matrices.
\[ I_3 = \begin{pmatrix} 1 & 0 & 0 \\0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} \]
\[ I_4 = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \]
They are called identity matrices because any matrix multiplied with an identity matrix equals itself. The diagonal entries of a matrix are the entries where the column and row number are the same. \(a_{2,2}\) is a diagonal entry but \(a_{3,5}\) is not. The trace of an n × n matrix is the sum of all the diagonal entries. In other words, for n × n matrix A, \(trace(A) = tr(A) = \sum_{i=1}^{n} a_{i,i}\) For example:
\[ trace(F) = tr(F) = tr \begin{pmatrix} 1 & 3 & 3\\ 0 & 6 & 7\\ -5 & 0 & 1 \end{pmatrix} = 1 + 6 + 1 = 8 \]
The trace has some useful properties, namely that for same size square matrices A and B and scalar c,
\[ tr(A) = tr(A^T)\] \[ tr(A + B) = tr(B + A) = tr(A) + tr(B)\] \[ tr(AB) = tr(BA)\] \[ tr(cA) = c*tr(A)\]
Determintants
The determinate of a square, 2 × 2 matrix A is
\[ det(A) = |A| = \begin{vmatrix} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{vmatrix} = a_{1,1} * a_{2,2} - a_{1,2}*a_{2,1}\]
For example
\[ det(A) = |A| = \begin{vmatrix} 5 & 2 \\ 7 & 2 \end{vmatrix} = 5*2 - 2*7 = -4\]
For a 3 × 3 matrix B, the determinate is
\[det(B) = |B| = \begin{vmatrix} b_{1,1} & b_{1,2} & b_{1,3}\\ b_{2,1} & b_{2,2} & b_{2,3}\\ b_{3,1} & b_{3,2} & b_{3,3} \end{vmatrix} = b_{1,3} \begin{vmatrix} b_{2,1} & b_{2,2}\\ b_{3,1} & b_{3,2} \end{vmatrix} - b_{2,3} \begin{vmatrix} b_{1,1} & b_{1,2}\\ b_{3,1} & b_{3,2} \end{vmatrix} + b_{3,3} \begin{vmatrix} b_{1,1} & b_{1,2} \\b_{2,1} & b_{2,2} \end{vmatrix}\]
\[ det(B) = b_{1,3}(b_{2,1} b_{3,2} - b_{2,2} b_{3,1} ) - b_{2,3}(b_{1,1} b_{3,2} - b_{1,2} b_{3,1} ) + b_{3,3}(b_{1,1} b_{2,2} - b_{1,2} b_{2,1} ) \]
For example:
\[det(B) = |B| = \begin{vmatrix} 4 & 0 & -1\\2 & -2 & 3 \\ 7 & 5 & 0 \end{vmatrix} = -1 \begin{vmatrix} 2 & -2\\ 7 & 5 \end{vmatrix} - 3 \begin{vmatrix} 4 & 0 \\7 & 5 \end{vmatrix} + 0 \begin{vmatrix} 4 & 0 \\ 2 & -2 \end{vmatrix}\]
\[ det(B) = -1 (2*5 - (-2)*7) + 3(4*5 - 0 *7) - 0 (4*(-2) - 0 * 2) = -1*24 - 3*20 + 0 *(-8) = -24 - 60 = -84 \]
In general, to find the determinate of a n \(\times\) n matrix, choose a row or column like column 1, and take the determinates of the "minor" matrices inside the original matrix, like so:
\[det(C) = |C| = \begin{vmatrix} c_{1,1} & c_{1,2} & \ldots & c_{1,n}\\ c_{2,1} & c_{2,2} & \ldots & c_{2,n}\\ \vdots & \vdots & \ddots & \vdots \\c_{n,1} & c_{.,2} & \ldots & c_{n,n} \end{vmatrix}\]
\[det(C) = (-1)^{1+1} c_{1,1} \begin{vmatrix} c_{2,2} & \ldots & c_{2,n}\\ \vdots & \ddots & \vdots \\ c_{n,2} & \ldots & c_{n,n} \end{vmatrix} + (-1)^{2+1} c_{2,1} \begin{vmatrix} c_{1,2} & \ldots & c_{1,n}\\ c_{3,2} & \ldots & c_{3,n}\\ \vdots & \ddots & \vdots\\ c_{n,2} & \ldots & c_{n,n} \end{vmatrix} + \ldots\]
\[ \ldots + (-1)^{n+1} c_{n,1} \begin{vmatrix} c_{1,2} & \ldots & c_{1,n}\\ \vdots & \ddots & \vdots \\ c_{n-1,2} & \ldots & c_{n-1,n} \end{vmatrix} \]
This is known as Laplace's formula,
\[ det(A) = \sum_{j=1}^{n} (-1)^{i+j} a_{i,j} det(A_{-i,-j}) = \sum_{i=1}^{n} (-1)^{i+j} a_{i,j} det(A_{-i,-j}) \]
For any i, j, where \(A_{-i,-j}\) is matrix A with row i and column j removed. This formula works whether one goes by rows, using the first formulation, or by columns, using the second formulation. It is easiest to use Laplace's formula when one chooses the row or column with the most zeroes.
Matrix Determinant Properties
The matrix determinate has some interesting properties.
\[det(I) = 1\]
where I is the identity matrix.
\[det(A) = det(A^T)\]
If A and B are square matrices with the same dimensions, then
\[ det(AB) = det(A)*det(B)\] and if A is a n × n square matrix and c is a scalar, then
\[ det(cA) = c^n det(A)\]
M.4 Matrix Inverse
M.4 Matrix Inverse- Inverse of a Matrix
-
The matrix B is the inverse of matrix A if \(AB = BA = I\). This is often denoted as \(B = A^{-1}\) or \(A = B^{-1}\). When taking the inverse of the product of two matrices A and B,
\[(AB)^{-1} = B^{-1} A^{-1}\]
When taking the determinate of the inverse of the matrix A,
\[ det(A^{-1}) = \frac{1}{det(A)} = det(A)^{-1}\]
Note that not all matrices have inverses. For a matrix A to have an inverse, that is to say for A to be invertible, A must be a square matrix and \(det(A) \neq 0\). For that reason, invertible matrices are also called nonsingular matrices.
Two examples are shown below
\[ det(A) = \begin{vmatrix} 4 & 5 \\ -2 & 1 \end{vmatrix} = 4*1-5*-2 = 14 \neq 0 \]
\[ det(C) = \begin{vmatrix} 1 & 2 & -1\\ 5 & 3 & 2 \\ 6 & 0 & 6 \end{vmatrix} = -2 \begin{vmatrix} 5 & 2 \\ 6 & 6 \end{vmatrix} + 3 \begin{vmatrix} 1 & -1\\ 6 & 6 \end{vmatrix} + 0 \begin{vmatrix} 1 & -1\\ 5 & 2 \end{vmatrix}\]
\[ det(C)= - 2(5*6-2*6) + 3(1*6-(-1)*6) - 0(1*2-(-1)*5) = 0 \]
So C is not invertible, because its determinate is zero. However, A is an invertible matrix, because its determinate is nonzero. To calculate that matrix inverse of a 2 × 2 matrix, use the below formula.
\[ A^{-1} = \begin{pmatrix} a_{1,1} & a_{1,2}\\ a_{2,1} & a_{2,2} \end{pmatrix} ^{-1} = \frac{1}{det(A)} \begin{pmatrix} a_{2,2} & -a_{1,2} \\ -a_{2,1} & a_{1,1} \end{pmatrix} = \frac{1}{a_{1,1} * a_{2,2} - a_{1,2}*a_{2,1}} \begin{pmatrix} a_{2,2} & -a_{1,2} \\ -a_{2,1} & a_{1,1} \end{pmatrix}\]
For example
\[ A^{-1} = \begin{pmatrix} 4 & 5 \\ -2 & 1 \end{pmatrix} ^{-1} = \frac{1}{det(A)} \begin{pmatrix} 1 & -5 \\ 2 & 4 \end{pmatrix} = \frac{1}{4*1 - 5*(-2)} \begin{pmatrix} 1 & -5 \\ 2 & 4 \end{pmatrix} = \begin{pmatrix} \frac{1}{14} & \frac{-5}{14} \\ \frac{2}{14} & \frac{4}{14} \end{pmatrix}\]
For finding the matrix inverse in general, you can use Gauss-Jordan Algorithm. However, this is a rather complicated algorithm, so usually one relies upon the computer or calculator to find the matrix inverse.
M.5 Advanced Matrix Properties
M.5 Advanced Matrix Properties- Orthogonal Vectors
-
Two vectors, x and y, are orthogonal if their dot product is zero.
For example
\[ e \cdot f = \begin{pmatrix} 2 & 5 & 4 \end{pmatrix} * \begin{pmatrix} 4 \\ -2 \\ 5 \end{pmatrix} = 2*4 + (5)*(-2) + 4*5 = 8-10+20 = 18\]
Vectors e and f are not orthogonal.
\[ g \cdot h = \begin{pmatrix} 2 & 3 & -2 \end{pmatrix} * \begin{pmatrix} 4 \\ -2 \\ 1 \end{pmatrix} = 2*4 + (3)*(-2) + (-2)*1 = 8-6-2 = 0\]
However, vectors g and h are orthogonal. Orthogonal can be thought of as an expansion of perpendicular for higher dimensions. Let \(x_1, x_2, \ldots , x_n\) be m-dimensional vectors. Then a linear combination of \(x_1, x_2, \ldots , x_n\) is any m-dimensional vector that can be expressed as
\[ c_1 x_1 + c_2 x_2 + \ldots + c_n x_n \]
where \(c_1, \ldots, c_n\) are all scalars. For example:
\[x_1 =\begin{pmatrix}
3 \\
8 \\
-2
\end{pmatrix},
x_2 =\begin{pmatrix}
4 \\
-2 \\
3
\end{pmatrix}\]
\[y =\begin{pmatrix}
-5 \\
12 \\
-8
\end{pmatrix} = 1*\begin{pmatrix}
3 \\
8 \\
-2
\end{pmatrix} + (-2)* \begin{pmatrix}
4 \\
-2 \\
3
\end{pmatrix} = 1*x_1 + (-2)*x_2\]
So y is a linear combination of \(x_1\) and \(x_2\). The set of all linear combinations of \(x_1, x_2, \ldots , x_n\) is called the span of \(x_1, x_2, \ldots , x_n\). In other words
\[ span(\{x_1, x_2, \ldots , x_n \} ) = \{ v| v= \sum_{i = 1}^{n} c_i x_i , c_i \in \mathbb{R} \} \]
A set of vectors \(x_1, x_2, \ldots , x_n\) is linearly independent if none of the vectors in the set can be expressed as a linear combination of the other vectors. Another way to think of this is a set of vectors \(x_1, x_2, \ldots , x_n\) are linearly independent if the only solution to the below equation is to have \(c_1 = c_2 = \ldots = c_n = 0\), where \(c_1 , c_2 , \ldots , c_n \) are scalars, and \(0\) is the zero vector (the vector where every entry is 0).
\[ c_1 x_1 + c_2 x_2 + \ldots + c_n x_n = 0 \]
If a set of vectors is not linearly independent, then they are called linearly dependent.
Example M.5.1
\[ x_1 =\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}, x_2 =\begin{pmatrix} 4 \\ -2 \\ 2 \end{pmatrix}, x_3 =\begin{pmatrix} 6 \\ 8 \\ -2 \end{pmatrix} \]
Does there exist a vector c, such that,
\[ c_1 x_1 + c_2 x_2 + c_3 x_3 = 0 \]
To answer the question above, let:
\begin{align} 3c_1 + 4c_2 +6c_3 &= 0,\\ 4c_1 -2c_2 + 8c_3 &= 0,\\ -2c_1 + 2c_2 -2c_3 &= 0 \end{align}
Solving the above system of equations shows that the only possible solution is \(c_1 = c_2 = c_3 = 0\). Thus \(\{ x_1 , x_2 , x_3 \}\) is linearly independent. One way to solve the system of equations is shown below. First, subtract (4/3) times the 1st equation from the 2nd equation.
\[-\frac{4}{3}(3c_1 + 4c_2 +6c_3) + (4c_1 -2c_2 + 8c_3) = -\frac{22}{3}c_2 = -\frac{4}{3}0 + 0 = 0 \Rightarrow c_2 = 0 \]
Then add the 1st and 3 times the 3rd equations together, and substitute in \(c_2 = 0\).
\[ (3c_1 + 4c_2 +6c_3) + 3*(-2c_1 + 2c_2 -2c_3) = -3c_1 + 10 c_2 = -3c_1 + 10*0 = 0 + 3*0 = 0 \Rightarrow c_1 = 0 \]
Now, substituting both \(c_1 = 0\) and \(c_2 = 0\) into equation 2 gives.
\[ 4c_1 -2c_2 + 8c_3 = 4*0 -2*0 + 8c_3 = 0 \Rightarrow c_3 = 0 \]
So \(c_1 = c_2 = c_3 = 0\), and \(\{ x_1 , x_2 , x_3 \}\) are linearly independent.
Example M.5.2
\[ x_1 =\begin{pmatrix} 1 \\ -8 \\ 8 \end{pmatrix}, x_2 =\begin{pmatrix} 4 \\ -2 \\ 2 \end{pmatrix}, x_3 =\begin{pmatrix} 1 \\ 3 \\ -2 \end{pmatrix} \]
In this case \(\{ x_1 , x_2 , x_3 \}\)are linearly dependent, because if \(c = (-1, 1, -2)\), then
\[c^T X = \begin{pmatrix}
-1 \\
1\\
-2
\end{pmatrix} \begin{pmatrix}
x_1 & x_2 & x_3
\end{pmatrix} = -1 \begin{pmatrix}
1 \\
-8\\
8
\end{pmatrix}+ 1
\begin{pmatrix}
4 \\
-2\\
2
\end{pmatrix} - 2 \begin{pmatrix}
1 \\
3 \\
-2
\end{pmatrix} =
\begin{pmatrix}
-1*1 +1*4-2*1 \\
-1*-8+1*-2-2*3 \\
-1*8+1*2-2*-2
\end{pmatrix}=
\begin{pmatrix}
0 \\
0 \\
0
\end{pmatrix}
\]
- Norm of a vector or matrix
-
The norm of a vector or matrix is a measure of the "length" of said vector or matrix. For a vector x, the most common norm is the \(\mathbf{L_2}\) norm, or Euclidean norm. It is defined as
\[ \| x \| = \| x \|_2 = \sqrt{ \sum_{i=1}^{n} x_i^2 } \]
Other common vector norms include the \(\mathbf{L_1}\) norm, also called the Manhattan norm and Taxicab norm.
\[ \| x \|_1 = \sum_{i=1}^{n} |x_i| \]
Other common vector norms include the Maximum norm, also called the Infinity norm.
\[ \| x \|_\infty = max( |x_1| ,|x_2|, \ldots ,|x_n|) \]
The most commonly used matrix norm is the Frobenius norm. For a m × n matrix A, the Frobenius norm is defined as:
\[ \| A \| = \| A \|_F = \sqrt{ \sum_{i=1}^{m} \sum_{j=1}^{n} x_{i,j}^2 } \]
- Quadratic Form of a Vector
-
The quadratic form of the vector x associated with matrix A is
\[ x^T A x = \sum_{i = 1}^{m} \sum_{j=1}^{n} a_{i,j} x_i x_j \]
A matrix A is Positive Definite if for any non-zero vector x, the quadratic form of x and A is strictly positive. In other words, \(x^T A x > 0\) for all nonzero x.
A matrix A is Positive Semi-Definite or Non-negative Definite if for any non-zero vector x, the quadratic form of x and A is non-negative . In other words, \(x^T A x \geq 0\) for all non-zero x. Similarly,
A matrix A is Negative Definite if for any non-zero vector x, \(x^T A x < 0\). A matrix A is Negative Semi-Definite or Non-positive Definite if for any non-zero vector x, \(x^T A x \leq 0\).
M.6 Range, Nullspace and Projections
M.6 Range, Nullspace and Projections- Range of a matrix
-
The range of m × n matrix A, is the span of the n columns of A. In other words, for
\[ A = [ a_1 a_2 a_3 \ldots a_n ] \]
where \(a_1 , a_2 , a_3 , \ldots ,a_n\) are m-dimensional vectors,
\[ range(A) = R(A) = span(\{a_1, a_2, \ldots , a_n \} ) = \{ v| v= \sum_{i = 1}^{n} c_i a_i , c_i \in \mathbb{R} \} \]
The dimension (number of linear independent columns) of the range of A is called the rank of A. So if 6 × 3 dimensional matrix B has a 2 dimensional range, then \(rank(A) = 2\).
For example
\[C =\begin{pmatrix}
1 & 4 & 1\\
-8 & -2 & 3\\
8 & 2 & -2
\end{pmatrix} = \begin{pmatrix}
x_1 & x_2 & x_3
\end{pmatrix}= \begin{pmatrix}
y_1 \\
y_2\\
y_3
\end{pmatrix}\]
C has a rank of 3, because \(x_1\), \(x_2\) and \(x_3\) are linearly independent.
- Nullspace
- p>The nullspace of a m \(\times\) n matrix is the set of all n-dimensional vectors that equal the n-dimensional zero vector (the vector where every entry is 0) when multiplied by A. This is often denoted as
\[N(A) = \{ v | Av = 0 \}\]
The dimension of the nullspace of A is called the nullity of A. So if 6 \(\times\) 3 dimensional matrix B has a 1 dimensional range, then \(nullity(A) = 1\).
The range and nullspace of a matrix are closely related. In particular, for m \(\times\) n matrix A,
\[\{w | w = u + v, u \in R(A^T), v \in N(A) \} = \mathbb{R}^{n}\]
\[R(A^T) \cap N(A) = \phi\]
This leads to the rank--nullity theorem, which says that the rank and the nullity of a matrix sum together to the number of columns of the matrix. To put it into symbols:
\[A \in \mathbb{R}^{m \times n} \Rightarrow rank(A) + nullity(A) = n\]
For example, if B is a 4 \(\times\) 3 matrix and \(rank(B) = 2\), then from the rank--nullity theorem, on can deduce that
\[rank(B) + nullity(B) = 2 + nullity(B) = 3 \Rightarrow nullity(B) = 1\]
- Projection
The projection of a vector x onto the vector space J, denoted by Proj(X, J), is the vector \(v \in J\) that minimizes \(\vert x - v \vert\). Often, the vector space J one is interested in is the range of the matrix A, and norm used is the Euclidian norm. In that case
\[Proj(x,R(A)) = \{ v \in R(A) | \vert x - v \vert_2 \leq \vert x - w \vert_2 \forall w \in R(A) \}\]
In other words
\[Proj(x,R(A)) = argmin_{v \in R(A)} \vert x - v \vert_2\]
M.7 Gauss-Jordan Elimination
M.7 Gauss-Jordan EliminationGauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. It relies upon three elementary row operations one can use on a matrix:
- Swap the positions of two of the rows
- Multiply one of the rows by a nonzero scalar.
- Add or subtract the scalar multiple of one row to another row.
For an example of the first elementary row operation, swap the positions of the 1st and 3rd row.
\[ \begin{pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \end{pmatrix}\Rightarrow \begin{pmatrix} 7 & 5 & 0 \\ 2 & -2 & 3 \\ 4 & 0 & -1 \end{pmatrix} \]
For an example of the second elementary row operation, multiply the second row by 3.
\[ \begin{pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \end{pmatrix} \Rightarrow \begin{pmatrix} 4 & 0 & -1 \\ 6 & -6 & 9 \\ 7 & 5 & 0 \end{pmatrix} \]
For an example of the third elementary row operation, add twice the 1st row to the 2nd row.
\[ \begin{pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \end{pmatrix}\Rightarrow \begin{pmatrix} 4 & 0 & -1 \\ 10 & -2 & 1 \\ 7 & 5 & 0 \end{pmatrix} \]
Reduced-row echelon form
The purpose of Gauss-Jordan Elimination is to use the three elementary row operations to convert a matrix into reduced-row echelon form. A matrix is in reduced-row echelon form, also known as row canonical form, if the following conditions are satisfied:
- All rows with only zero entries are at the bottom of the matrix
- The first nonzero entry in a row, called the leading entry or the pivot, of each nonzero row is to the right of the leading entry of the row above it.
- The leading entry, also known as the pivot, in any nonzero row is 1.
- All other entries in the column containing a leading 1 are zeroes.
For example
\[A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 3 \\ 0 & 0 & 0 \end{pmatrix}, B = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}, C = \begin{pmatrix} 0 & 7 & 3 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, D = \begin{pmatrix} 1 & 7 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \]
Matrices A and B are in reduced-row echelon form, but matrices C and D are not. C is not in reduced-row echelon form because it violates conditions two and three. D is not in reduced-row echelon form because it violates condition four. In addition, the elementary row operations can be used to reduce matrix D into matrix B.
Steps for Gauss-Jordan Elimination
To perform Gauss-Jordan Elimination:
- Swap the rows so that all rows with all zero entries are on the bottom
- Swap the rows so that the row with the largest, leftmost nonzero entry is on top.
- Multiply the top row by a scalar so that top row's leading entry becomes 1.
- Add/subtract multiples of the top row to the other rows so that all other entries in the column containing the top row's leading entry are all zero.
- Repeat steps 2-4 for the next leftmost nonzero entry until all the leading entries are 1.
- Swap the rows so that the leading entry of each nonzero row is to the right of the leading entry of the row above it.
Selected video examples are shown below:
- Gauss-Jordan Elimination - Jonathan Mitchell (YouTube)
- Using Gauss-Jordan to Solve a System of Three Linear Equations - Example 1 - patrickJMT (YouTube)
- Algebra - Matrices - Gauss Jordan Method Part 1 Augmented Matrix - IntuitiveMath (YouTube)
- Gaussian Elimination - patrickJMT (YouTube)
To obtain the inverse of a n × n matrix A :
- Create the partitioned matrix \(( A | I )\) , where I is the identity matrix.
- Perform Gauss-Jordan Elimination on the partitioned matrix with the objective of converting the first part of the matrix to reduced-row echelon form.
- If done correctly, the resulting partitioned matrix will take the form \(( I | A^{-1} )\)
- Double-check your work by making sure that \(AA^{-1} = I\).
M.8 Eigendecomposition
M.8 Eigendecomposition- Eigenvector of a matrix
An eigenvector of a matrix A is a vector whose product when multiplied by the matrix is a scalar multiple of itself. The corresponding multiplier is often denoted as \(lambda\) and referred to as an eigenvalue. In other words, if A is a matrix, v is a eigenvector of A, and \(\lambda\) is the corresponding eigenvalue, then \(Av = \lambda v\).
For Example
\[ A= \begin{pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \end{pmatrix} \]
\[ v = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} \]
\[ Av = \begin{pmatrix} 4 & 0 & 1 \\ 2 & -2 & 3 \\ 5 & 7 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 4*1 + 0*1 + 1*2 \\ 2*1+ -2*1+ 3*2 \\ 5*1+ 7*1+ 0*2 \end{pmatrix} = \begin{pmatrix} 6 \\ 6 \\ 12 \end{pmatrix} = 6v \]
In the above example, v is an eigenvector of A, and the corresponding eigenvalue is 6. To find the eigenvalues/vectors of a n × n square matrix, solve the characteristic equation of a matrix for the eigenvalues. This equation is
\[ det(A - \lambda I ) = 0\]
Where A is the matrix, \(\lambda\) is the eigenvalue, and I is an n × n identity matrix. For example, take
\[ A= \begin{pmatrix} 4 & 3 \\ 2 & -1 \end{pmatrix}\]
The characteristic equation of A is listed below.
\[ det(A - \lambda I ) = det( \begin{pmatrix} 4 & 3 \\ 2 & -1 \end{pmatrix} - \lambda \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} ) = det \begin{pmatrix} 4 - \lambda & 3 \\ 2 & -1 - \lambda \end{pmatrix} = 0 \]
\[ det(A - \lambda I ) = (4 - \lambda)(-1 - \lambda) - 3*2 = \lambda^2 - 3 \lambda - 10 = (\lambda + 2)(\lambda - 5) = 0 \]
Therefore, one finds that the eigenvalues of A must be -2 and 5. Once the eigenvalues are found, one can then find the corresponding eigenvectors from the definition of an eigenvector. For \(\lambda = 5\), simply set up the equation as below, where the unknown eigenvector is \(v = (v_1, v_2)'\).
\[\begin{pmatrix} 4 & 3 \\ 2 & -1 \end{pmatrix} * \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} = 5 \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} \]
\[\begin{pmatrix} 4 v_1 + 3 v_2 \\ 2 v_1 - 1 v_2 \end{pmatrix} = \begin{pmatrix} 5 v_1 \\ 5 v_2 \end{pmatrix} \]
And then solve the resulting system of linear equations to get
\[ v = \begin{pmatrix} 3 \\ 1 \end{pmatrix} \]
For \(\lambda = -2\), simply set up the equation as below, where the unknown eigenvector is \(w = (w_1, w_2)\).
\[\begin{pmatrix} 4 & 3 \\ 2 & -1 \end{pmatrix} * \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} = -2 \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} \]
\[\begin{pmatrix} 4 w_1 + 3 w_2 \\ 2 w_1 - 1 w_2 \end{pmatrix} = \begin{pmatrix} -2 w_1 \\ -2 w_2 \end{pmatrix} \]
And then solve the resulting system of linear equations to get
\[ w = \begin{pmatrix} -1 \\ 2 \end{pmatrix} \]
M.9 Self-Assess
M.9 Self-AssessHere's your chance to assess what you remember from the matrix review.
- Review the concepts and methods on the pages in this section. Note the courses that certain sections are aligned with as prerequisites:
STAT 414 STAT 501 STAT 504 STAT 505 M.1 - Matrix Definitions Required Required Required Required M.2 - Matrix Arithmetic Required Required Required Required M.3 - Matrix Properties Required Required Required Required M.4 - Matrix Inverse Required Required Required Required M.5 - Advanced Topics Recommended Recommended Recommended 5.1, 5.4, Required
5.2, 5.3, Recommended - Download and Complete the Matrix Self-Assessment Exam.
- Determine your Score by Reviewing the Matrix Self-Assessment Exam Solutions.
Students that score below 70% (fewer than 21 questions correct) should consider a further review of these materials and are strongly encouraged to take MATH 220 (2 credits) or an equivalent course.
If you have struggled with the concepts and methods that are presented here, you will indeed struggle in the courses above that expect this foundation.
Please Note: These materials are NOT intended to be a complete treatment of the ideas and methods used in Matrix algebra. These materials and the accompanying self-assessment are simply intended as simply an 'early warning signal' for students. Also, please note that completing the self-assessment successfully does not automatically ensure success in any of the courses that use this foundation.