3.4 - Analysis of Variance: The Basic Idea
- Break down the total variation in y ("total sum of squares") into two components:
- a component that is "due to" the change in x ("regression sum of squares")
- a component that is just due to random error ("error sum of squares")
- If the regression sum of squares is a "large" component of the total sum of squares, it suggests that there is a linear association between the predictor x and the response y.
Here is a simple picture illustrating how the distance \(y_i-\bar{y}\) is decomposed into the sum of two distances, \(\hat{y}_i-\bar{y}\) and \(y_i-\hat{y}_i\). Roll your cursor over each of the three components of the equation at the bottom of the graphic below to see what each of the the values represents geometrically.
Although the derivation isn't as simple as it seems, the decomposition holds for the sum of the squared distances, too:
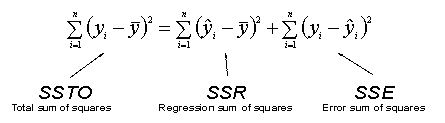
SSTO = SSR + SSE
The degrees of freedom associated with each of these sums of squares follow a similar decomposition.
- You might recognize SSTO as being the numerator of the sample variance. Recall that the denominator of the sample variance is n-1. Therefore, n-1 is the degrees of freedom associated with SSTO.
- Recall that the mean square error MSE is obtained by dividing SSE by n-2. Therefore, n-2 is the degrees of freedom associated with SSE.
Then, we obtain the following breakdown of the degrees of freedom:
|
(n - 1)
|
=
|
( 1 )
|
+
|
(n - 2)
|
|
degrees of freedom associated with SSTO
|
degrees of freedom associated with SSR
|
degrees of freedom associated with SSE
|

