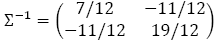1(b).2.1: Measures of Similarity and Dissimilarity
Similarity and Dissimilarity
Distance or similarity measures are essential to solve many pattern recognition problems such as classification and clustering. Various distance/similarity measures are available in literature to compare two data distributions. As the names suggest, a similarity measures how close two distributions are. For multivariate data complex summary methods are developed to answer this question.
Similarity Measure
- Numerical measure of how alike two data objects are.
- Often falls between 0 (no similarity) and 1 (complete similarity).
Dissimilarity Measure
- Numerical measure of how different two data objects are.
- Range from 0 (objects are alike) to ∞ (objects are different).
Proximity refers to a similarity or dissimilarity.
Similarity/Dissimilarity for Simple Attributes
Here, p and q are the attribute values for two data objects.
| Attribute Type | Similarity | Dissimilarity |
| Nominal | \(s=\begin{cases} 1 & \text{ if } p=q \\ 0 & \text{ if } p\neq q \end{cases}\) |
\(d=\begin{cases} 0 & \text{ if } p=q \\ 1 & \text{ if } p\neq q \end{cases}\) |
| Ordinal |
\(s=1-\frac{\left \| p-q \right \|}{n-1}\) (values mapped to integer 0 to n-1, where n is the number of values) |
\(d=\frac{\left \| p-q \right \|}{n-1}\) |
| Interval or Ratio | \(s=1-\left \| p-q \right \|, s=\frac{1}{1+\left \| p-q \right \|}\) | \(d=\left \| p-q \right \|\) |
Common Properties of Dissimilarity Measures
Distance, such as the Euclidean distance, is a dissimilarity measure and has some well known properties:
- d(p, q) ≥ 0 for all p and q, and d(p, q) = 0 if and only if p = q,
- d(p, q) = d(q,p) for all p and q,
- d(p, r) ≤ d(p, q) + d(q, r) for all p, q, and r, where d(p, q) is the distance (dissimilarity) between points (data objects), p and q.
A distance that satisfies these properties is called a metric.Following is a list of several common distance measures to compare multivariate data. We will assume that the attributes are all continuous.
Euclidean Distance
Assume that we have measurements xik, i = 1, … , N, on variables k = 1, … , p (also called attributes).
The Euclidean distance between the ith and jth objects is
\[d_E(i, j)=\left(\sum_{k=1}^{p}\left(x_{ik}-x_{jk} \right) ^2\right)^\frac{1}{2}\]
for every pair (i, j) of observations.
The weighted Euclidean distance is
\[d_{WE}(i, j)=\left(\sum_{k=1}^{p}W_k\left(x_{ik}-x_{jk} \right) ^2\right)^\frac{1}{2}\]
If scales of the attributes differ substantially, standardization is necessary.
Minkowski Distance
The Minkowski distance is a generalization of the Euclidean distance.
With the measurement, xik , i = 1, … , N, k = 1, … , p, the Minkowski distance is
\[d_M(i, j)=\left(\sum_{k=1}^{p}\left | x_{ik}-x_{jk} \right | ^ \lambda \right)^\frac{1}{\lambda}, \]
where λ ≥ 1. It is also called the Lλ metric.
- λ = 1 : L1 metric, Manhattan or City-block distance.
- λ = 2 : L2 metric, Euclidean distance.
- λ → ∞ : L∞ metric, Supremum distance.
\[ \lim{\lambda \to \infty}=\left( \sum_{k=1}^{p}\left | x_{ik}-x_{jk} \right | ^ \lambda \right) ^\frac{1}{\lambda} =\text{max}\left( \left | x_{i1}-x_{j1}\right| , ... , \left | x_{ip}-x_{jp}\right| \right) \]
Note that λ and p are two different parameters. Dimension of the data matrix remains finite.
Mahalanobis Distance
Let X be a N × p matrix. Then the ith row of X is
\[x_{i}^{T}=\left( x_{i1}, ... , x_{ip} \right)\]
The Mahalanobis distance is
\[d_{MH}(i, j)=\left( \left( x_i - x_j\right)^T \Sigma^{-1} \left( x_i - x_j\right)\right)^\frac{1}{2}\]
where ∑ is the p×p sample covariance matrix.
Self-check
Think About It!
Calculate the answers to these questions by yourself and then click the icon on the left to reveal the answer.
1. We have \(X= \begin{pmatrix}
1 & 3 & 1 & 2 & 4\\
1 & 2 & 1 & 2 & 1\\
2 & 2 & 2 & 2 & 2
\end{pmatrix}\).
- Calculate the Euclidan distances.
- Calculate the Minkowski distances (λ=1 and λ→∞ cases).
2. We have \(X= \begin{pmatrix}
2 & 3 \\
10 & 7 \\
3 & 2
\end{pmatrix}\).
- Calculate the Minkowski distance (λ = 1, λ = 2, and λ → ∞ cases) between the first and second objects.
- Calculate the Mahalanobis distance between the first and second objects.
Common Properties of Similarity Measures
Similarities have some well known properties:
- s(p, q) = 1 (or maximum similarity) only if p = q,
- s(p, q) = s(q, p) for all p and q, where s(p, q) is the similarity between data objects, p and q.
Similarity Between Two Binary Variables
The above similarity or distance measures are appropriate for continuous variables. However, for binary variables a different approach is necessary.

Simple Matching and Jaccard Coefficients
- Simple matching coefficient = (n1,1+ n0,0) / (n1,1 + n1,0 + n0,1 + n0,0).
- Jaccard coefficient = n1,1 / (n1,1 + n1,0 + n0,1).

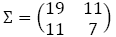 we have
we have