9.1.3 - Example - Diabetes Dataset
This is the Pima Indians diabetes dataset we used before in Lesson 3.5. The input X is two dimensional. The two variables \(X_1\) and \(X_2\) are the first two principal components of the original 8 variables.
There are two classes: without diabetes \((Y=0)\); with diabetes \((Y=1)\). To avoid confusion, we'll label the class variable, G, the same way (so \(G=0\) corresponds to \(Y=0\) and \(G=1\) corresponds to \(Y=1\)).
Applying logistic regression, we obtain
\(\beta = (–0.7682, 0.6816, 0.3663)^T\).
Typically in logistic regression we focus on the probability equation for \(Y=1\), which in this case can be rewritten as:
\[ Pr(G=1|X=x) =\frac{e^{\beta_0+\beta_1X_1+\beta_2X_2}}{1+e^{\beta_0+\beta_1X_1+\beta_2X_2}}=\frac{1}{1+e^{-\beta_0-\beta_1X_1-\beta_2X_2}}. \]
The posterior probabilities based on the estimated parameters are therefore:
\[ \begin {align} Pr(G=1|X=x) & =\frac{e^{-0.7682+0.6816X_1+0.3663X_2}}{1+e^{-0.7682+0.6816X_1+0.3663X_2}} =\frac{1}{1+e^{0.7682-0.6816X_1-0.3663X_2}} \\ Pr(G=0|X=x) & =1-Pr(G=1|X=x) \end {align} \]
The classification rule based on a 0.5 probability cut-off is:
\[\hat{G}(x) = \left\{\begin{matrix}
0 & \text{if } 0.7682-0.6816X_1-0.3663X_2 \ge 0\\
1 & \text{if } 0.7682-0.6816X_1-0.3663X_2 < 0
\end{matrix}\right. \]
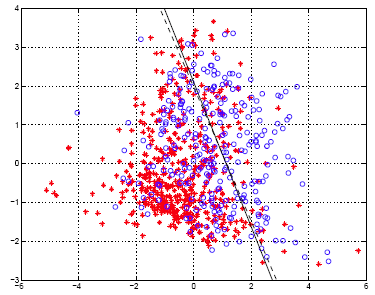
In the following scatter plot, we show the classification boundary obtained by logistic regression and compare it to that by LDA. Solid line: decision boundary obtained by logistic regression. Dash line: decision boundary obtained by LDA. Red cross: without diabetes (class 0). Blue circle: with diabetes (class 1).
The performance of the logistic regression classification is as follows.
- QDA within training data classification error rate: 28.13%.
- Sensitivity: 45.90%.
- Specificity: 85.80%.
We obtain the classifier and apply it to the training data set and see what percentage of data are classified incorrectly because we know the true labels in the training data.
By sensitivity we mean that if the person has diabetes what percentage of the data points will say that they actually have diabetes. In other words, if it is in fact a positive case, percentage of the times that we will classify it as a positive case.
This refers to the percentage of correctness of negative samples. If the person does not have diabetes, what percentage of the times that we classify them as not having diabetes.

