Let's start by first considering the case in which the two random variables under consideration, \(X\) and \(Y\), say, are both discrete. We'll jump in right in and start with an example, from which we will merely extend many of the definitions we've learned for one discrete random variable, such as the probability mass function, mean and variance, to the case in which we have two discrete random variables.
Example 17-1 Section

Suppose we toss a pair of fair, four-sided dice, in which one of the dice is RED and the other is BLACK. We'll let:
- \(X\) = the outcome on the RED die = \(\{1, 2, 3, 4\}\)
- \(Y\) = the outcome on the BLACK die = \(\{1, 2, 3, 4\}\)
What is the probability that \(X\) takes on a particular value \(x\), and \(Y\) takes on a particular value \(y\)? That is, what is \(P(X=x, Y=y)\)?
Solution
Just as we have to in the case with one discrete random variable, in order to find the "joint probability distribution" of \(X\) and \(Y\), we first need to define the support of \(X\) and \(Y\). Well, the support of \(X\) is:
\(S_1=\{1, 2, 3, 4\}\)
And, the support of \(Y\) is:
\(S_2=\{1, 2, 3, 4\}\)
Now, if we let \((x,y)\) denote one of the possible outcomes of one toss of the pair of dice, then certainly (1, 1) is a possible outcome, as is (1, 2), (1, 3) and (1, 4). If we continue to enumerate all of the possible outcomes, we soon see that the joint support S has 16 possible outcomes:
\(S=\{(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4)\}\)
Now, because the dice are fair, we should expect each of the 16 possible outcomes to be equally likely. Therefore, using the classical approach to assigning probability, the probability that \(X\) equals any particular \(x\) value, and \(Y\) equals any particular \(y\) value, is \(\frac{1}{16}\). That is, for all \((x,y)\) in the support \(S\):
\(P(X=x, Y=y)=\frac{1}{16}\)
Because we have identified the probability for each \((x, y)\), we have found what we call the joint probability mass function. Perhaps, it is not too surprising that the joint probability mass function, which is typically denoted as \(f(x,y)\), can be defined as a formula (as we have above), as a graph, or as a table. Here's what our joint p.m.f. would like in tabular form:
Now that we've found our first joint probability mass function, let's formally define it now.
- Joint Probability Mass Function
- Let \(X\) and \(Y\) be two discrete random variables, and let \(S\) denote the two-dimensional support of \(X\) and \(Y\). Then, the function \(f(x,y)=P(X=x, Y=y)\) is a joint probability mass function (abbreviated p.m.f.) if it satisfies the following three conditions:
-
\(0 \leq f(x,y) \leq 1\)
-
\(\mathop{\sum\sum}\limits_{(x,y)\in S} f(x,y)=1\)
-
\(P[(X,Y) \in A]=\mathop{\sum\sum}\limits_{(x,y)\in A} f(x,y)\) where \(A\) is a subset of the support \(S\).
The first condition, of course, just tells us that each probability must be a valid probability number between 0 and 1 (inclusive). The second condition tells us that, just as must be true for a p.m.f. of one discrete random variable, the sum of the probabilities over the entire support \(S\) must equal 1. The third condition tells us that in order to determine the probability of an event \(A\), you simply sum up the probabilities of the \((x,y)\) values in \(A\).
Now, if you take a look back at the representation of our joint p.m.f. in tabular form, you can see that the last column contains the probability mass function of \(X\) alone, and the last row contains the probability mass function of \(Y\) alone. Those two functions, \(f(x)\) and \(f(y)\), which in this setting are typically referred to as marginal probability mass functions, are obtained by simply summing the probabilities over the support of the other variable. That is, to find the probability mass function of \(X\), we sum, for each \(x\), the probabilities when \(y=1, 2, 3, \text{ and } 4\). That is, for each \(x\), we sum \(f(x, 1), f(x, 2), f(x, 3), \text{ and }f(x, 4)\). Now that we've seen the two marginal probability mass functions in our example, let's give a formal definition of a marginal probability mass function.
- Marginal Probability Mass Function of \(X\)
-
Let \(X\) be a discrete random variable with support \(S_1\), and let \(Y\) be a discrete random variable with support \(S_2\). Let \(X\) and \(Y\) have the joint probability mass function \(f(x, y)\) with support \(S\). Then, the probability mass function of \(X\) alone, which is called the marginal probability mass function of \(X\), is defined by:
\(f_X(x)=\sum\limits_y f(x,y)=P(X=x),\qquad x\in S_1\)
where, for each \(x\) in the support \(S_1\), the summation is taken over all possible values of \(y\). Similarly, the probability mass function of \(Y\) alone, which is called the marginal probability mass function of \(Y\), is defined by:
\(f_Y(y)=\sum\limits_x f(x,y)=P(Y=y),\qquad y\in S_2\)
where, for each \(y\) in the support \(S_2\), the summation is taken over all possible values of \(x\).
If you again take a look back at the representation of our joint p.m.f. in tabular form, you might notice that the following holds true:
\(P(X=x,Y=y)=\dfrac{1}{16}=P(X=x)\cdot P(Y=y)=\dfrac{1}{4} \cdot \dfrac{1}{4}=\dfrac{1}{16}\)
for all \(x\in S_1, y\in S_2\). When this happens, we say that \(X\) and \(Y\) are independent. A formal definition of the independence of two random variables \(X\) and \(Y\) follows.
- Independent and Dependent Random Variables
-
The random variables \(X\) and \(Y\) are independent if and only if:
\(P(X=x, Y=y)=P(X=x)\times P(Y=y)\)
for all \(x\in S_1, y\in S_2\). Otherwise, \(X\) and \(Y\) are said to be dependent.
Now, suppose we were given a joint probability mass function \(f(x, y)\), and we wanted to find the mean of \(X\). Well, one strategy would be to find the marginal p.m.f of \(X\) first, and then use the definition of the expected value that we previously learned to calculate \(E(X)\). Alternatively, we could use the following definition of the mean that has been extended to accommodate joint probability mass functions.
Definition. Let \(X\) be a discrete random variable with support \(S_1\), and let \(Y\) be a discrete random variable with support \(S_2\). Let \(X\) and \(Y\) be discrete random variables with joint p.m.f. \(f(x,y)\) on the support \(S\). If \(u(X,Y)\) is a function of these two random variables, then:
\(E[u(X,Y)]=\mathop{\sum\sum}\limits_{(x,y)\in S} u(x,y)f(x,y)\)
if it exists, is called the expected value of \(u(X,Y)\). If \(u(X,Y)=X\), then:
\(\mu_X=E[X]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} xf(x,y)\)
if it exists, is the mean of \(X\). If \(u(X,Y)=Y\), then:
\(\mu_Y=E[Y]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} yf(x,y)\)
if it exists, is the mean of \(Y\).
Example 17-1 (continued) Section
Consider again our example in which we toss a pair of fair, four-sided dice, in which one of the dice is RED and the other is BLACK. Again, letting:
- \(X\) = the outcome on the RED die = \(\{1, 2, 3, 4\}\)
- \(Y\) = the outcome on the BLACK die = \(\{1, 2, 3, 4\}\)
What is the mean of \(X\) ? And, what is the mean of \(Y\)?
Solution
The mean of \(X\) is calculated as:
\(\mu_X=E[X]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} xf(x,y) =1\left(\dfrac{1}{16}\right)+\cdots+1\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)\)
which simplifies to:
\(\mu_X=E[X]=1\left(\dfrac{4}{16}\right)+2\left(\dfrac{4}{16}\right)+3\left(\dfrac{4}{16}\right)+4\left(\dfrac{4}{16}\right)=\dfrac{40}{16}=2.5\)
The mean of \(Y\) is similarly calculated as:
\(\mu_Y=E[Y]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} yf(x,y)=1\left(\dfrac{1}{16}\right)+\cdots+1\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)+\cdots+4\left(\dfrac{1}{16}\right)\)
which simplifies to:
\(\mu_Y=E[Y]=1\left(\dfrac{4}{16}\right)+2\left(\dfrac{4}{16}\right)+3\left(\dfrac{4}{16}\right)+4\left(\dfrac{4}{16}\right)=\dfrac{40}{16}=2.5\)
By the way, you probably shouldn't find it surprising that the formula for the mean of \(X\) reduces to:
\(\mu_X=\sum\limits_{x\in S_1} xf(x)\)
because:
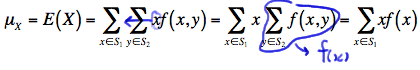
That is, the third equality holds because the x values don't depend on \(y\) and therefore can be pulled through the summation over \(y\). And, the last equality holds because of the definition of the marginal probability mass function of \(X\). Similarly, the mean of \(Y\) reduces to:
\(\mu_Y=\sum\limits_{y\in S_2} yf(y)\)
because:
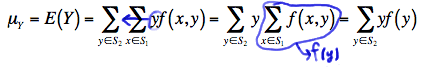
That is, again, the third equality holds because the y values don't depend on \(x\) and therefore can be pulled through the summation over \(x\). And, the last equality holds because of the definition of the marginal probability mass function of \(Y\).
Now, suppose we were given a joint probability mass function \(f(x,y)\), and we wanted to find the variance of \(X\). Again, one strategy would be to find the marginal p.m.f of \(X\) first, and then use the definition of the expected value that we previously learned to calculate \(\text{Var}(X)\). Alternatively, we could use the following definition of the variance that has been extended to accommodate joint probability mass functions.
Definition. Let \(X\) be a discrete random variable with support \(S_1\), and let \(Y\) be a discrete random variable with support \(S_2\). Let \(X\) and \(Y\) be discrete random variables with joint p.m.f. \(f(x,y)\) on the support \(S\). If \(u(X,Y)\) is a function of these two random variables, then:
\(E[u(X,Y)]=\mathop{\sum\sum}\limits_{(x,y)\in S} u(x,y)f(x,y)\)
if it exists, is called the expected value of \(u(X,Y)\). If \(u(X,Y)=(X-\mu_X)^2\), then:
\(\sigma^2_X=Var[X]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} (x-\mu_X)^2 f(x,y)\)
if it exists, is the variance of \(X\). The variance of \(X\) can also be calculated using the shortcut formula:
\(\sigma^2_X=E(X^2)-\mu^2_X=\left(\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} x^2 f(x,y)\right)-\mu^2_X\)
If \(u(X,Y)=(Y-\mu_Y)^2\), then:
\(\sigma^2_Y=Var[Y]=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} (y-\mu_Y)^2 f(x,y)\)
if it exists, is the variance of \(Y\). The variance of \(Y\) can also be calculated using the shortcut formula:
\(\sigma^2_Y=E(Y^2)-\mu^2_Y=\left(\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} y^2 f(x,y)\right)-\mu^2_Y\)
Example 17-1 (continued again) Section
Consider yet again our example in which we toss a pair of fair, four-sided dice, in which one of the dice is RED and the other is BLACK. Again, letting:
- \(X\) = the outcome on the RED die = \(\{1, 2, 3, 4\}\)
- \(Y\) = the outcome on the BLACK die = \(\{1, 2, 3, 4\}\)
What is the variance of \(X\) ? And, what is the variance of \(Y\)?
Solution
Using the definition, the variance of \(X\) is calculated as:
\(\sigma^2_X=\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} (x-\mu_X)^2 f(x,y)=(1-2.5)^2\left(\dfrac{1}{16}\right)+\cdots+(4-2.5)^2\left(\dfrac{1}{16}\right)=1.25\)
Thankfully, we get the same answer using the shortcut formula for the variance of \(X\):
\(\sigma^2_X=E(X^2)-\mu^2_X=\left(\sum\limits_{x\in S_1} \sum\limits_{y\in S_2} x^2 f(x,y)\right)-\mu^2_X=\left[1^2 \left(\dfrac{1}{16}\right)+\cdots+4^2 \left(\dfrac{1}{16}\right)\right]-2.5^2=\dfrac{120}{16}-6.25=1.25\)
Calculating the variance of \(Y\) is left for you as an exercise. You should, because of the symmetry, also get \(\text{Var}(Y)=1.25\).