As the name of this section suggests, we will now spend some time learning how to find the probability distribution of functions of random variables. For example, we might know the probability density function of \(X\), but want to know instead the probability density function of \(u(X)=X^2\). We'll learn several different techniques for finding the distribution of functions of random variables, including the distribution function technique, the change-of-variable technique and the moment-generating function technique.

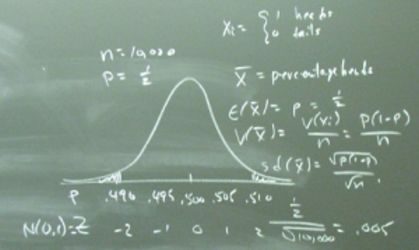
The more important functions of random variables that we'll explore will be those involving random variables that are independent and identically distributed. For example, if \(X_1\) is the weight of a randomly selected individual from the population of males, \(X_2\) is the weight of another randomly selected individual from the population of males, ..., and \(X_n\) is the weight of yet another randomly selected individual from the population of males, then we might be interested in learning how the random function:

\(\bar{X}=\dfrac{X_1+X_2+\cdots+X_n}{n}\)

is distributed. We'll first learn how \(\bar{X}\) is distributed assuming that the \(X_i\)'s are normally distributed. Then, we'll strip away the assumption of normality, and use a classic theorem, called the Central Limit Theorem, to show that, for large \(n\), the function:

\(\dfrac{\sqrt{n}(\bar{X}-\mu)}{\sigma}\)

approximately follows the standard normal distribution. Finally, we'll use the Central Limit Theorem to use the normal distribution to approximate discrete distributions, such as the binomial distribution and the Poisson distribution.