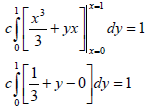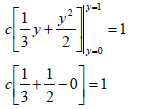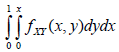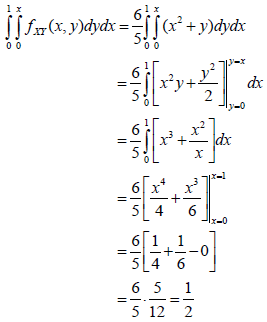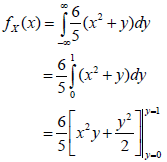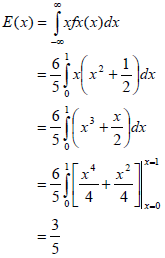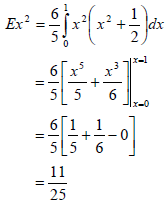Example
A hat contains four chips labeled 1, 2, 3, and 4. Suppose we draw two such chips from the hat randomly and with replacement. Let X denote the smallest number of the two chips drawn, and let Y denote the largest number of the two chips drawn.
value of x | fY | |||||
1 | 2 | 3 | 4 | |||
value of y | 1 | 1/16 | N/A | N/A | N/A | 1/16 |
2 | 2/16 | 1/16 | N/A | N/A | 3/16 | |
3 | 2/16 | 2/16 | 1/16 | N/A | 5/16 | |
4 | 2/16 | 2/16 | 2/16 | 1/16 | 7/16 | |
fX | 7/16 | 5/16 | 3/16 | 1/16 | 16/16 | |
Example
Let ![]() for the support where x ∈ {1, 2, 3} and y ∈ {1, 2}.
for the support where x ∈ {1, 2, 3} and y ∈ {1, 2}.
What if we needed to find the probability that X1 + X2 is equal to some value, such as P(X1 + X2 = 3). We want to look at when both of these are happening at the same time so there is only a limited range of possibilities. Here we have written this out in terms of the possibilities within the joint pmf, (1, 2) and (2, 1). Then we plugged in the values and found the probability.
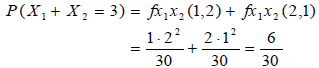
The point of this example is to show why the joint pmf is critical for doing things like this. If we had the marginal pmf we would not be able to do this problem. You need the joint pmf. If you knew the marginal probabilities for X1 and X2 separately you would have no clue how to do this type of problem.
Now that we have the joint pmf, let's determine the marginal for X1. First we write out the basic definition and sum over 1, 2. We use the same formula and plug in these new values.
for the possible values of x ∈ {1, 2, 3}
Example
![]() for x ∈ (0, 1) and y ∈ (0, 1). What is the value of the "normalizing constant" c?
for x ∈ (0, 1) and y ∈ (0, 1). What is the value of the "normalizing constant" c?
Now we can take the c constant out and calculate the first integral with respect to x and then simply.
Next, we do the integral with respect to y.
So,
(This should be a review of your basic calculus!)
Now we know what the density is. What can we do with this?
Suppose we were asked the question, what is P(Y < X)? How do we go about solving this question?
The variables are not discrete because they live on a continuum from 0 to 1. But we are constraining this such that X must be greater than Y .
We need to use this formula: ![]() and to do this we need to find out what A is. This is the same as saying P(Y < X) = P((x, y) ∈ A) and is a joint distribution where we are looking for all of the pairs where y is less than A. We need to write down what y needs to satisfy and what x needs to satisfy.
and to do this we need to find out what A is. This is the same as saying P(Y < X) = P((x, y) ∈ A) and is a joint distribution where we are looking for all of the pairs where y is less than A. We need to write down what y needs to satisfy and what x needs to satisfy.
You need y to be less than x and you need y to live between 0 and 1. Therefore, y must be between 0 to x.
What does x need to satisfy? It simply need to be between 0 and 1. By constraining y, x is taken care of.
Once we have this, the rest of the problem becomes simple calculus. We will do the y first, specifying that y go from 0 to x, and x goes from 0 to 1. This is how we have translated the P((x, y) ∈ A) into this statement below for this problem.
Next we plug in the 6/5 for c and the rest of the double integral and then follow through with the calculations of each integral.
So, we have done the first probability calculation for the joint density.
Let's check something before we move on.
Why did we integrate with respect to y first and then x second? Would it make a difference if they were switched?
Let's try the alternative and interchange the order of the integration (first x and then y). How would we do this? We would need to solve this problem for a different set, B where we will integrate this first with respect to x and then with respect to y as follows.
We are need to re-write the set out for B such that we describe the limits for integration: B = {(x, y): x ∈ (y, 1), y ∈ (0, 1)}. x is going from yto 1 tells us that x is larger than y and less than 1. x is taken care of and y can be anything in the range (0, 1). This is the exact same set as Athat we looked at earlier, it is just different in the order in which it is written. Now we can write the double integral:
for support x ∈ (y, 1), y ∈ (0, 1)
There is no need to work through this calculation. We get the same answer.
In all of these problems, setting up the integration is the difficult part. The rest is just following through on the calculation.
Analogous to dealing with joint distributions with discrete random variables, let's find the marginal pdf's from the joint pdf. Whereas previously we had summed over the variables, here what we will do is "integrate out" with respect to the other variable. Take a look at the following:
, and similarly
Note: The joint pdf specifies all the marginal pdf's, but the marginal pdf's do not specify the joint pdf.
Let's work through the same example to demonstrate this:
Example
Our example remains ![]() with support x ∈ (0, 1), y ∈ (0, 1). You can then find the marginal pdf by just using the definition and move forward with the calculation such as pulling out the constant and then adapting the limits to meet the needs of the support as follows:
with support x ∈ (0, 1), y ∈ (0, 1). You can then find the marginal pdf by just using the definition and move forward with the calculation such as pulling out the constant and then adapting the limits to meet the needs of the support as follows:
The result of this is the following pdf
for x ∈ (0, 1).
We can do the same thing for y.
for y ∈ (0, 1).
Now we have both of the marginal pdfs. And, once you have the marginals you now know both the distributions of x and y separately.
Can you answer this question now? What is the expected value of x, E(X)? Yes we can, because we can use the denisity we just derived to find the expectation of x separately.
So, the E(X) = 3/5.
What about the variance? We know how to find this using:
We already have EX, so all we need to find is Ex2:
Therefore,
Next, let's think about independence. How do we know if these two are independent of one another?
Definition: If X and Y have a joint pdf, fXY(x, y), then X and Y are independent if and only if:
fXY(x, y) = fX(x)fY(y) for all x and y.
This should look very familiar. Let's go back to our example again and see if this is true.
Example
for x, y ∈ (0, 1).
Are they independent? If you multiply fX(x) and fY(y), (11/25 × 3/5), we will not get fXY(x, y).
Therefore, ![]() . They are not the same so they are not independent.
. They are not the same so they are not independent.
There is a trick that you can use here. If you look at the joint distribution, and if you can write this as a product of terms that contain only one and something that contain only the other, and the support is rectangular, then they are not independent.
Another Example
for x, y ∈ (0, 1).
In fact, X,Y are independent. The shortcut: are independent if and only if you can write fXY(x, y) as the product of two functions, gx × hy, of just the x's and just the y's.
For some functions, g and h (that depend only on x and y respectively) and the support is rectangular.