The underlying theme of sample size calculation in all clinical trials is precision. ; Validity and unbiasedness do not necessarily relate to sample size.

Usually, sample size is calculated with respect to two circumstances. The first involves precision for an estimator, e.g., requiring a 95% confidence interval for the population mean to be within ± \(\delta\) units. The second involves statistical power for hypothesis testing, e.g., requiring 0.80 or 0.90 statistical power \(\left(1- \beta\right)\) for a hypothesis test when the significance level (\(\alpha\)) is 0.05 and the effect size (the clinically meaningful effect) is \(\Delta\) units.

The formulae for many sample size calculations will involve percentiles from the standard normal distribution. The graph below illustrates the 2.5^th percentile and the 97.5^th percentile.

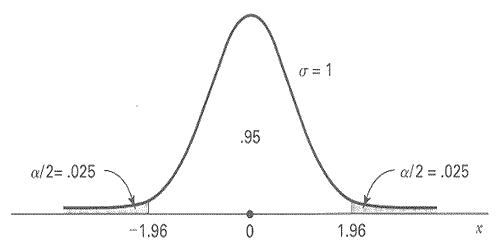
Fig. 1 Standard normal distribution centered on zero.

For a two-sided hypothesis test with significance level α and statistical power \(1 - \beta\), the percentiles of interest are \(z_{(1-\alpha/2)}\) and \(z_{(1 - \beta)}\).

For a one-sided hypothesis test, \(z_{(1 - \alpha)}\) is used instead. Usual choices of \(\alpha\) are 0.05 and 0.01, and usual choices of \(\beta\) are 0.20 and 0.10, so the percentiles of interest usually are:

\( z_{0.995} = 2.58, z_{0.99} = 2.33, z_{0.975} = 1.96, z_{0.95} = 1.65, z_{0.90} = 1.28, z_{0.80} = 0.84 \).

In SAS, the PROBIT function is available to generate percentiles from the standard normal distribution function, e.g., Z = PROBIT(0.99) yields a value of 2.33 for Z. So, if you ever need to generate z-values you can get SAS to do this for you.

It is important to realize that sample size calculations are approximations. The assumptions that are made for the sample size calculation, e.g., the standard deviation of an outcome variable or the proportion of patients who succeed with placebo, may not hold exactly.

Also, we may base the sample size calculation on a t statistic for a hypothesis test, which assumes an exact normal distribution of the outcome variable when it only may be approximately normal.

In addition, there will be loss-to-follow-up, so not all of the subjects who initiate the study will provide complete data. .Some will deviate from the protocol, including not taking the assigned treatment or adding on a treatment. Sample size calculations and recruitment of subjects should reflect these anticipated realities.