After completing a statistical test, conclusions are drawn about the null hypothesis. In cases where the null hypothesis is not rejected, a researcher may still feel that the treatment did have an effect. Let's say that three weight loss treatments are conducted. At the end of the study, the researcher analyzes the data and finds there are no differences among the treatments. The researcher believes that there really are differences. While you might think this is just wishful thinking on the part of the researcher, there MAY be a statistical reason for the lack of significant findings.
At this point, the researcher can run a power analysis. More specifically, this would be a retrospective power analysis as it is done after the experiment was completed. Recall from your introductory text or course, that power is the ability to reject the null when the null is really false. The factors that impact power are sample size (larger samples lead to more power), the effect size (treatments that result in larger differences between groups are more readily found), the variability of the experiment, and the significance of the type 1 error.
As a note, the most common type of power analysis are those that calculate needed sample sizes for experimental designs. These analyses take advantage of pilot data or previous research. When power analysis is done ahead of time it is a prospective power analysis.
Typically, we want power to be at 80%. Again, power represents our ability to reject the null when it is false, so a power of 80% means that 80% of the time our test identifies a difference in at least one of the means correctly. The converse of this is that 20% of the time we risk not rejecting the null when we really should be.
Using our greenhouse example, we can run a retrospective power analysis. (Just a reminder we typically don't do this unless we have some reason to suspect the power of our test was very low.) This is one analysis where Minitab is much easier and still just as accurate as SAS, so we will use Minitab to illustrate this simple power analysis in detail and follow up the analysis with SAS.
Power Analysis
In Minitab select STAT > Power and Sample Size > One-Way ANOVA
Since we have a one-way ANOVA we select this test (you can see there are power analyses for many different tests and SAS will allow even more complicated options).
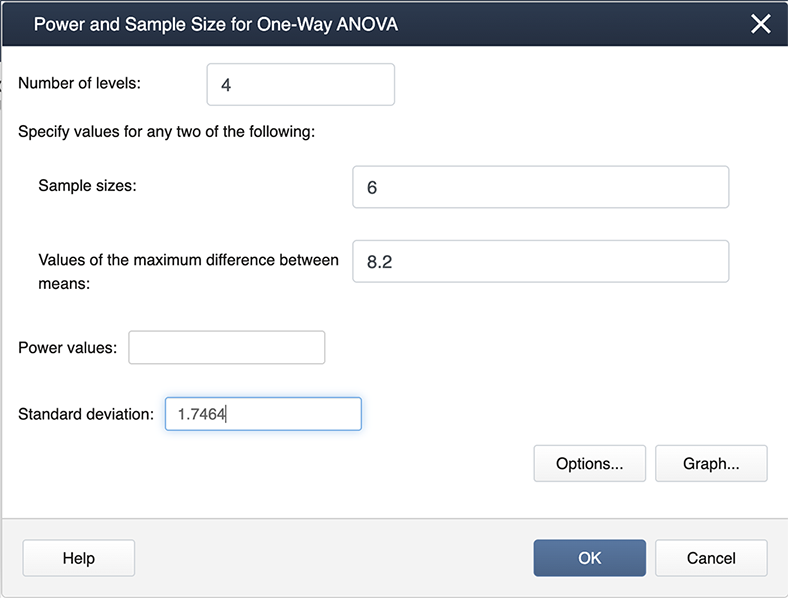
When you look at our filled-in dialogue box you notice we have not entered a value for power. This is because Minitab will calculate whichever box you leave blank (so if we needed sample size we would leave sample size blank and fill in a value for power). From our example, we know the number of levels is 4 because we have four treatments. We have six observations for each treatment so the sample size is 6. The value for the maximum difference in the means is 8.2 (we simply subtracted the smallest mean from the largest mean, and the standard deviation is 1.747. Where did this come from? The MSE, available from the ANOVA table, is about 3, and hence the standard deviation =sqrt(3)=1.747).
After we click OK we get the following output:
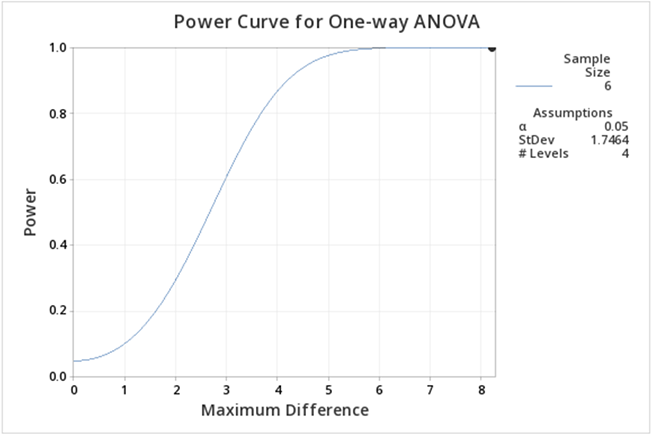
If you follow this graph you see that power is on the y-axis and the power for the specific setting is indicated by a black dot. It is hard to find, but if you look carefully the black dot corresponds to a power of 1. In practice, this is very unusual, but can be easily explained given that the greenhouse data was constructed to show differences.
We can ask the question, what about differences among the treatment groups, not considering the control? All we need to do is modify some of the input in Minitab.
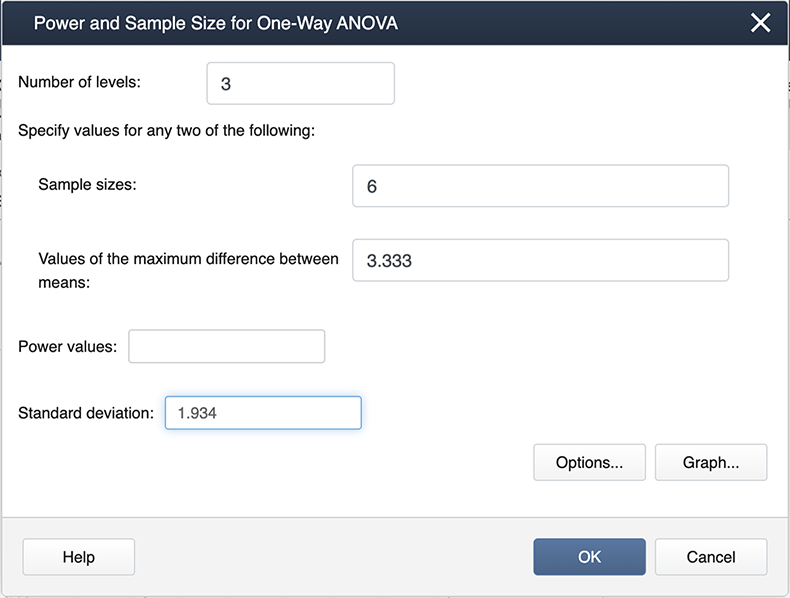
Note the differences here as in the previous screenshot. We now have 3 levels because we are only considering the three treatments. The maximum differences between the means and also the standard deviation are also different.
The output now is much easier to see:
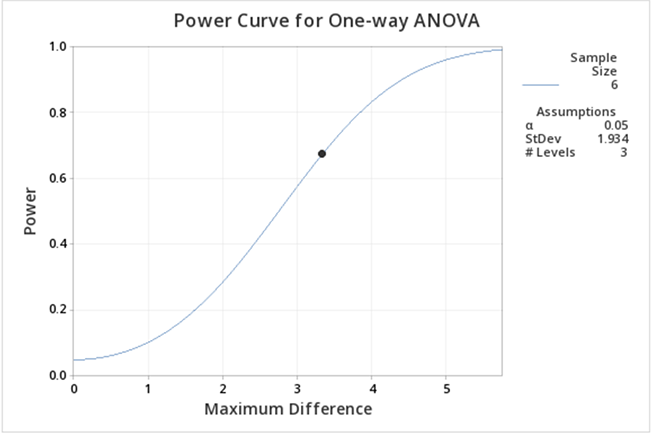
Here we can see the power is lower than when including the control. The main reason for this decrease is that the difference between the means is smaller.
You can experiment with the power function in Minitab to provide you with sample sizes, etc. for various powers. Below is some sample output when we ask for various power curves for various sample sizes, a kind of "what if" scenario.
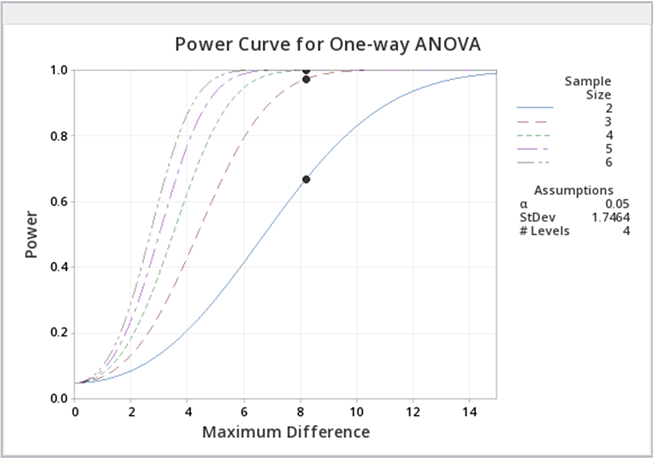
Just as a reminder, power analyses are most often performed BEFORE an experiment is conducted, but occasionally, power analysis can provide some evidence as to why significant differences were not found.
Let us now consider running the power analysis in SAS. In our greenhouse example with 4 treatments (control, F1, F2, and F3) the estimated means were \(21, 28.6, 25.877, 29.2\) respectively. Using ANOVA the estimated standard deviation of errors was \(1.747\) (which is obtained by \(\sqrt{MSE} = \sqrt{3.0517}\). There are 6 replicates for each treatment. Using these values we could employ SAS POWER procedure to compute the power of our study retrospectively.
proc power;
onewayanova alpha=.05 test=overall
groupmeans=(21 28.6 25.87 29.2)
npergroup=6 stddev=1.747
power=.;
run;
| Fixed Scenario Elements | |
|---|---|
| Method | Exact |
| Alpha | 0.05 |
| Group Means | 21 28.6 25.87 29.2 |
| Standard Deviation | 1.747 |
| Sample Size per Group | 6 |
| Computed Power |
|---|
| Power |
| >.999 |
As with MINITAB, we see that the retrospective power analysis for our greenhouse example yields a power of 1. If we re-do the analysis ignoring the CONTROL treatment group, then we only have 3 treatment groups: F1, F2, and F3. The ANOVA with only these three treatments yields an MSE of \(3.735556\). Therefore the estimated standard deviation of errors would be \(1.933\). We will have a power of 0.731 in this modified scenario as shown in the below output.
| Fixed Scenario Elements | |
|---|---|
| Method | Exact |
| Alpha | 0.05 |
| Group Means | 28.6 25.87 29.2 |
| Standard Deviation | 1.933 |
| Sample Size per Group | 6 |
| Computed Power |
|---|
| Power |
| 0.731 |
Suppose we ask the question: how many replicates we would need to obtain at least 80% power in greenhouse example with the same group means but with different variability in data (i.e. standard deviations should be different)? We can use SAS POWER to answer this question. For example, using the estimated standard deviation 1.747, we can calculate the number of needed replicates as follows.
proc power;
onewayanova alpha=.05 test=overall
groupmeans=(21 28.6 25.87 29.2)
npergroup=. stddev=1.747
power=.8;
run;
| Fixed Scenario Elements | |
|---|---|
| Method | Exact |
| Alpha | 0.05 |
| Group Means | 21 28.6 25.87 29.2 |
| Standard Deviation | 1.747 |
| Nominal Power | 0.8 |
| Computed N per Group | |
|---|---|
| Actual Power | N per Group |
| 0.991 | 3 |
We can see that with a standard deviation of 1.747, if we have only 3 replicates in each of the four treatments, we can detect the differences in greenhouse example means with more than 80% power. However, as data get noisier (i.e. as standard deviation increases) we will need more replicates to achieve 80% power in the same example.
Continuing the R example found in the previous section, we can obtain the power analysis of the greenhouse example. First, reproduce the ANOVA table (defined in the previous section).
aov3 # equivalent to print(aov3)
Anova Table (Type III tests)
Response: height
Sum Sq Df F value Pr(>F)
(Intercept) 16432.7 1 5384.817 < 2.2e-16 ***
fert 251.4 3 27.465 2.712e-07 ***
Residuals 61.0 20
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The between and within-group variances are needed to conduct the power analysis. The within-group variance can be estimated using the MSE, calculated from the SSE and df outputs of the table. More specifically:
within.var = aov3$`Sum Sq`[3]/aov3$Df[3]
within.var
[1] 3.051667
The between-group variance can be calculated from the group means. These were calculated in the previous section using the emmeans function. We reproduce the output here:
lsmeans # equivalent to print(lsmeans)
fert emmean SE df lower.CL upper.CL Control 21.0 0.713 20 19.5 22.5 F1 28.6 0.713 20 27.1 30.1 F2 25.9 0.713 20 24.4 27.4 F3 29.2 0.713 20 27.7 30.7 Confidence level used: 0.95
Thus we calculate the between-group variance:
groupmeans = summary(lsmeans)$emmean
between.var = var(groupmeans)
between.var
[1] 13.96889
Inputting also the number of groups (4) and the number of replicates within each group (n=6), we use the following command to obtain the power analysis:
power.anova.test(groups=4,n=6,between.var=between.var,within.var=within.var)
Balanced one-way analysis of variance power calculation
groups = 4
n = 6
between.var = 13.96889
within.var = 3.051667
sig.level = 0.05
power = 1
NOTE: n is number in each group
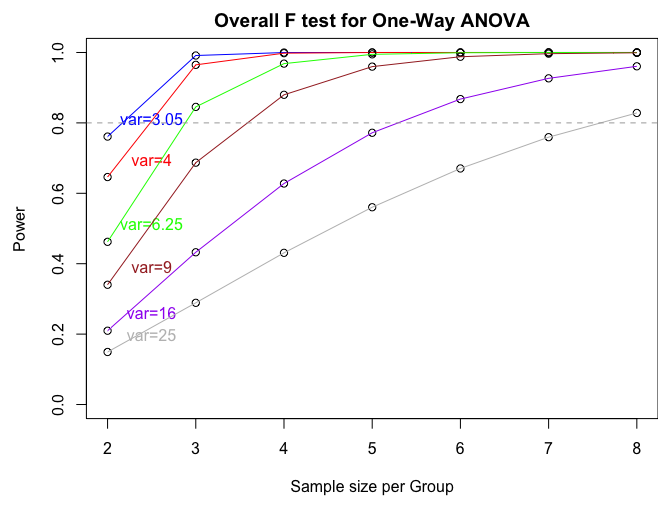
If we want to produce a power plot by increasing sample size and the variance (like the one produced by SAS) we can use the following commands:
n = seq(2,8,by=1)
p = power.anova.test(groups=4,n=n,between.var=between.var,within.var=within.var)
p1 = power.anova.test(groups=4,n=n,between.var=between.var,within.var=4)
p2 = power.anova.test(groups=4,n=n,between.var=between.var,within.var=6.25)
p3 = power.anova.test(groups=4,n=n,between.var=between.var,within.var=9)
p4 = power.anova.test(groups=4,n=n,between.var=between.var,within.var=16)
p5 = power.anova.test(groups=4,n=n,between.var=between.var,within.var=25)
par(mfcol=c(1,1),mar=c(4.5,4.5,2,0))
plot(n,p$power,ylab="Power",xlab="Sample size per Group",main="Overall F test for One-Way ANOVA", ylim=c(0,1))
lines(n,p$power, col = "blue")
text(2.5,p$power[1]+0.05,"var=3.05",col="blue")
points(n,p1$power)
lines(n,p1$power, col = "red")
text(2.5,p1$power[1]+0.05,"var=4",col="red")
points(n,p2$power)
lines(n,p2$power, col = "green")
text(2.5,p2$power[1]+0.05,"var=6.25",col="green")
points(n,p3$power)
lines(n,p3$power, col = "brown")
text(2.5,p3$power[1]+0.05,"var=9",col="brown")
points(n,p4$power)
lines(n,p4$power, col = "purple")
text(2.5,p4$power[1]+0.05,"var=16",col="purple")
points(n,p5$power)
lines(n,p5$power, col = "gray")
text(2.5,p5$power[1]+0.05,"var=25",col="gray")
abline(h=0.80,lty=2,col="dark gray")