After identifying the experimental unit and the number of replications that will be used, the next step is to assign the treatments (i.e. factor levels or factor level combinations) to the experimental units.
In a completely randomized design (CRD), treatments are assigned to experimental units at random. This is typically done by listing the treatments and assigning a random number to each.
In the greenhouse experiment discussed in lesson 1, there was a single factor (fertilizer) with 4 levels (i.e. 4 treatments), six replications, and a total of 24 experimental units (potted plants). Suppose the image below is the greenhouse bench (viewed from above) that was used for the experiment.
We need to be able to randomly assign each of the treatment levels to 6 potted plants. To do this, we first assign numbers to the physical position of the pots on the bench.
Next, we randomly assign the 24 total treatments (4 treatment levels, replicated 6 times) to the potted plants. Examples of how this can be done using statistical software are found below.
Using Technology Section
To make the assignments in SAS we can utilize the SAS surveyselect procedure seen below.
proc surveyselect data=greenhouse out=trtassignment outrandom
method=srs
samprate=1;
run;
The output would be as below. In practice, it is recommended to specify a seed to ensure the results are reproducible.
| Obs | Fertilizer |
|---|---|
| 1 | F3 |
| 2 | F2 |
| 3 | Con |
| 4 | F2 |
| 5 | F3 |
| 6 | Con |
| 7 | F2 |
| 8 | F2 |
| 9 | F3 |
| 10 | F1 |
| 11 | F1 |
| 12 | F3 |
| 13 | F2 |
| 14 | F1 |
| 15 | F3 |
| 16 | F3 |
| 17 | F1 |
| 18 | Con |
| 19 | Con |
| 20 | F2 |
| 21 | Con |
| 22 | F1 |
| 23 | Con |
| 24 | F1 |
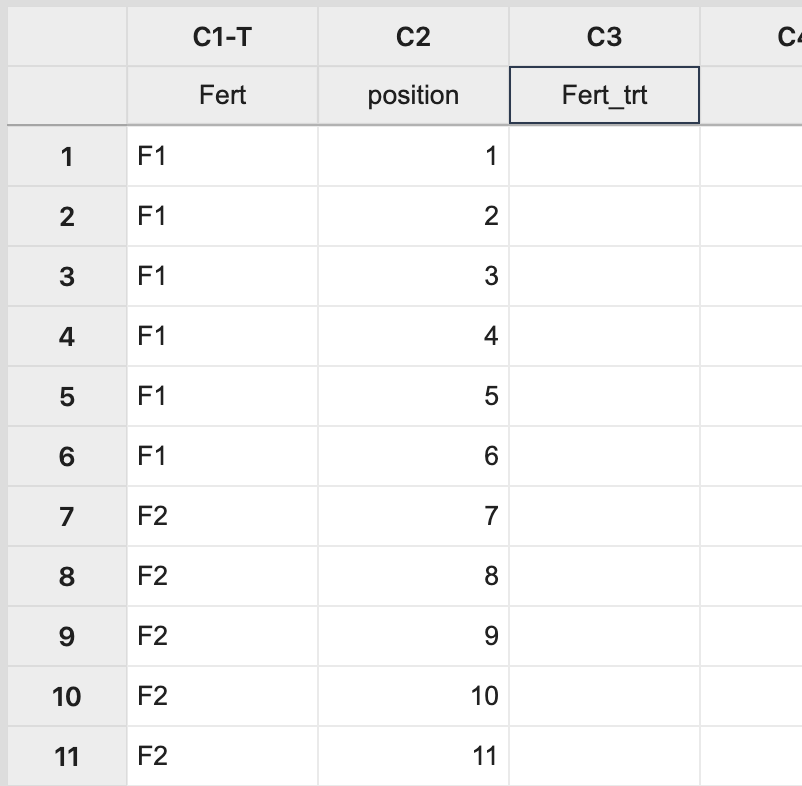
Next, select Calc > Sample from Columns, fill in the dialog box as seen below, and click OK.
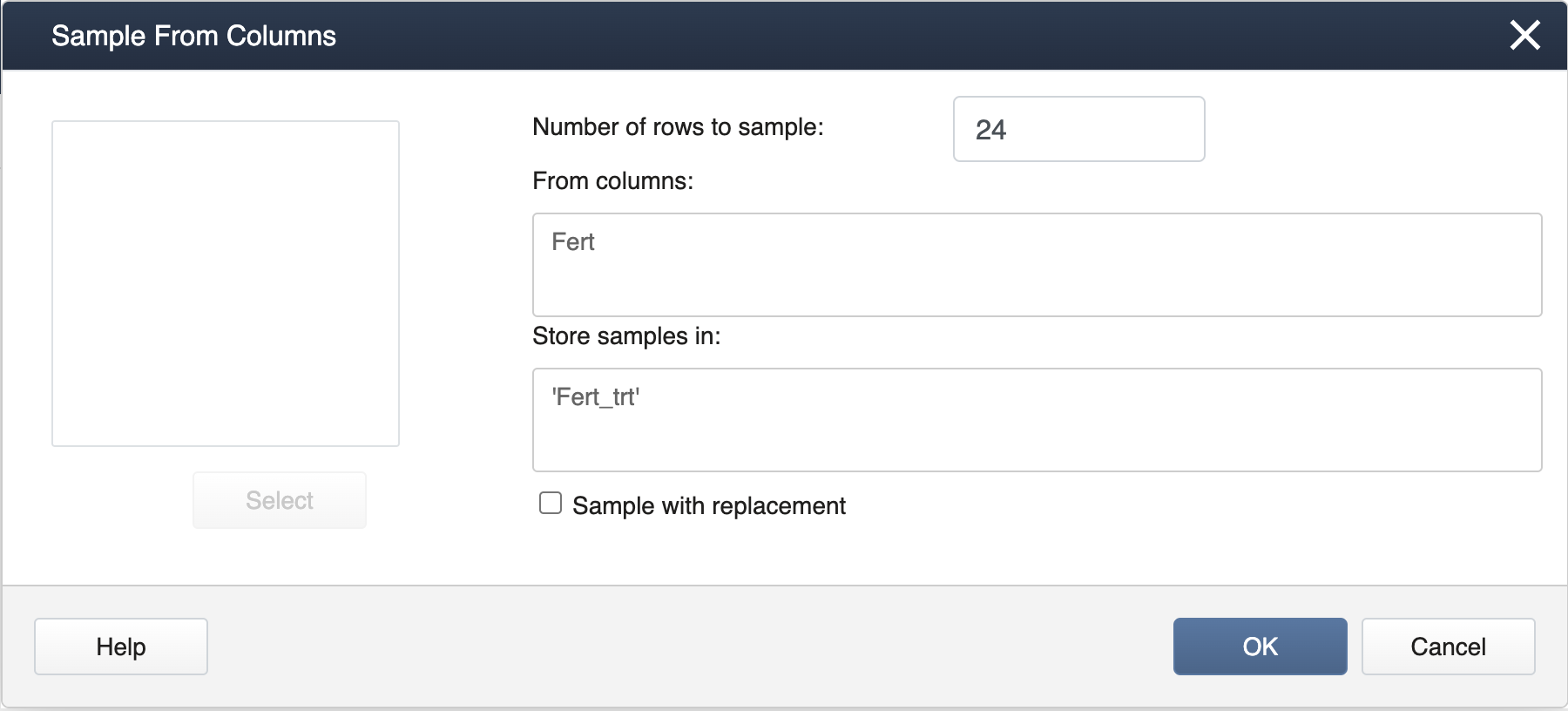
This will result in a completely random assignment.
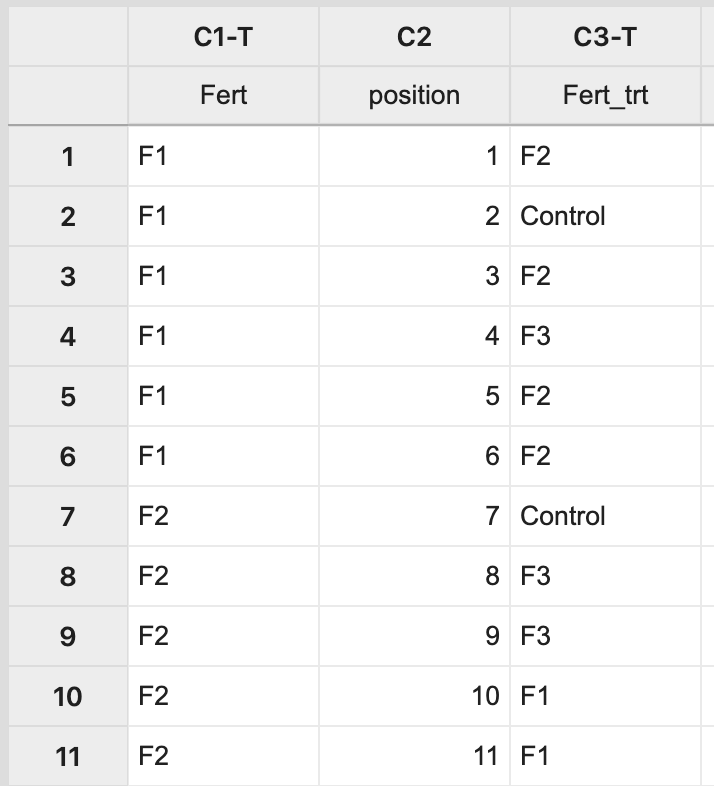
This assignment can then be used to apply the treatment levels appropriately to pots on the greenhouse bench.
To randomly assign treatment levels to each of our plants in R, we first create a vector containing all the possible treatments, then randomly sample from the vector to create the assignment.
trt_levels = c("F1","F2","F3","Control")
treatments = rep(trt_levels,6)
set.seed(1)
trt_assign = sample(treatments)
data.frame(trt_assign)
trt_assign 1 Control 2 F3 3 F1 4 F2 5 F3 6 F2 7 F2 8 F2 9 F1 10 Control 11 F2 12 F2 13 F3 14 F3 15 F1 16 F3 17 Control 18 F1 19 Control 20 Control 21 F1 22 F1 23 F3 24 Control