Foldover designs are useful when you are involved in sequentially testing a set of factors. You begin with very small experiments and proceed in stages. We consider this type of design through two examples.
1/8th fractional factorial of a \(2^6\) design
First, we will look at an example with 6 factors and we select a \(2^{6-3}\) design, or a 1/8th fractional factorial of a \(2^6\) design.
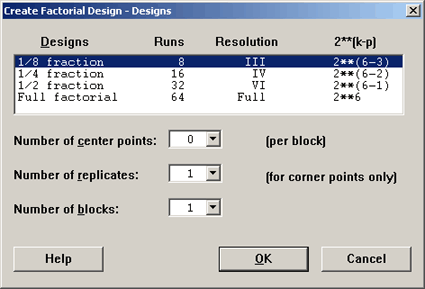
In order to select a 1/8 fraction of the full factorial, we will need to choose 3 generators and make sure that the generalized interactions among these three generators are of sufficient size to achieve the higher resolution. In this case it will be a Resolution III as Minitab shows us above.
Let's remind ourselves how we do this. We can choose I = ABD = ACE = BCF as the generators.
Since \(N = 2^{6-3} = 2^3\) observations, we start with a basic \(2^3\) design which would be set up using the following framework. First write down the complete factorial for factors A, B, and C. From that we can generate additional factors based on the available interactions, i.e. we will make D = AB, E = AC, and F = BC. Complete the table below ...
| trt | A | B | C | D = AB | E = AC | F = BC | ABC |
|---|---|---|---|---|---|---|---|
| (1) | - |
-
|
-
|
||||
| a |
+
|
- |
-
|
||||
| b | - | + | - | ||||
| ab |
+
|
+
|
- | ||||
| c | - |
-
|
+ | ||||
| ac |
+
|
- | + | ||||
| bc | - | + |
+
|
||||
| abc |
+
|
+
|
+
|
Our generators are ABD, ACE and BCF. So, our alias structure is created by this equivalence:
I = ABD = ACE = BCF
If these are our generators then all of the generalized interactions among these terms are also part of the generator set. Let's take a look at them:
The 2-way interactions:
- ABD × ACE = BCDE,
- ABD × BCF = ACDF,
- ACE × BCF = ABEF,
and the 3-way interaction:
- ABD × ACE × BCF = DEF
We still have a Resolution III design because the generator set is composed of words, the smallest of which has 3 letters. So you could fill in the framework above for these factors just by multiplying from the basic design, the pluses and minuses.
Minitab does this for you. And the worksheet will look like this:
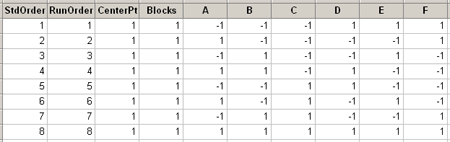
We can estimate all of the main effects and one of the aliased two-way interactions. What this also suggests is that there is one more factor that we could include in a design of this size, N = 8.
1/16th fraction of a \(2^7\) design Section
Now we consider a 1/16th fraction of a \(2^7\) design or a \(2^{7-4}\) design. Again, we will have only \(N = 2^3 = 8\) observations but now we have seven factors. Thus \(k = 7\) and \(p = 4\).
Let's look at this in Minitab - for seven factors here are the design options ...
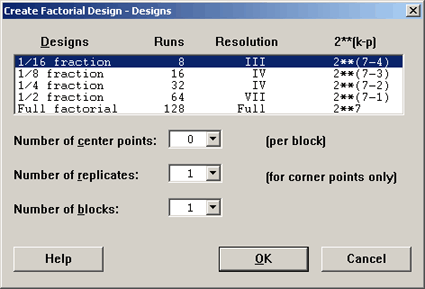
The 1/16 fraction design is a Resolution III design and it is the smallest possible one. Here is what the design looks like:
Fractional Factorial Design
| Factors: | 7 | Base Design: | 7, 8 | Resolution: | III |
| Runs: | 8 | Replicates: | 1 | Fraction: | 1/16 |
| Blocks: | 1 | Center pts (total): | 0 | ||
* NOTE * Some main effects are confounded with two-way interactions.
Design Generators: D = AB, E = AC, F = BC, G = ABC
Alias Structure
I + ABD + ACE + AFG + BCF + BEG + CDG + DEF + ABCG + ABEF + ACDF + ADEG + BCDE + BDFG + CEFG + ABCDEFG
A + BD + CD + FG + BCG + BEF + CDF + DEG + ABCF + ABEG + ACDG + ADEF + ABCDE + ABDFG + ACEFG + BCDEFG
B + AD + CF + EG + ACG + AEF + CDE + DFG + ABCE + ABFG + BCDG + BDEF + ABCDF + ABDEG + GCEFG + ACDEFG
C + AE + BF + DG + ABG + ADF + BDE + EFG + ABCD + ACFG + BCEG + CDEF + ABCEF + ACDEG + BCDFG + ABDEFG
D + AB + CG + EF + ACF + AEG + BCE + BFG + ACDE + ADFG + BCDF + BDEG + ABCDG + ABDEF + CDEFG + ABCEFG
E + AC + BG + DF + ABF + ADG + BCD + CFG + ABDE + AEFG + BCEF + CDEG + ABCEG + ACDEF + BDEFG + ABCDFG
F + AG + BC + DE + ABE + ACD + BDG + CEG + ABDF + ACEF + BEFG + CDFG + ABCFG + ADEFG + BCDEF + ABCDEG
G + AF + BE + CD + ABC + ADE + BDF + CEF + ABDG + ACEG + BCFG + DEFG + ABEFG + ACDFG + BCDEG + ABCDEF
The generators are listed on top. The same first three are as before and then G = ABC, the only one left. The alias structure gets quite convoluted. The reason being that if we were taking a complete replicate of this design, \(2^7\), we could put it into 16 blocks. In this case,we are only looking at one of the 16 blocks in the complete design. In these 16 blocks there are 15 degrees of freedom among these blocks. So, you see I + the 15 effects.
Sometimes people are not interested in seeing all of these higher order interactions after all five-way interactions are not all that interesting. You can clean up this output a bit by using this option found in the 'Results...' dialog box in Minitab:
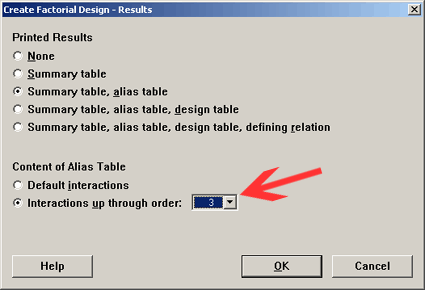
Notice now that the only thing you find in the table are main effects. No 2-way interactions are available. This is a unique design called a Saturated Design. This is the smallest possible design that you could use for 7 factors. Another way to look at this is that for a design with eight observations the maximum number of factors you can include in that design is seven. We are using every degree of freedom to estimate the main effects.
If we moved to the next smallest design where \(N = 16\), then what would the saturated design be? 15 factors. You would have a \(2^{15-11}\), which would give us a \(2^4\) basic design. Then we could estimate up to 15 main effects.
So, you can see with fairly small designs, only 16 observations, we can test for a lot of factors if we are only interested in main effects, using a Resolution III design. Let's see what the options are in Minitab.
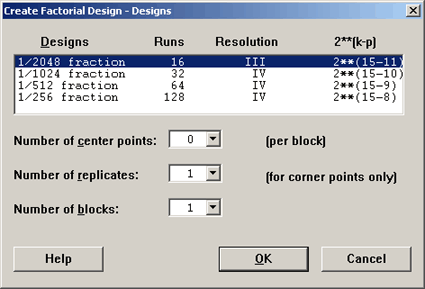
Notice that the largest design shown has 128 runs which is already a very large experiment for 15 factors. You probably wouldn't want more than that.
Folding a Design Section
We will come back to Saturated designs - but first let's consider the \(2^{7-4}\) design, which is saturated and is a Resolution III design and let's fold it over.
Let's assume we ran this design, we found some interesting effects but we have no degrees of freedom for error.So we want to look at another replicate of this design. Rather than repeating this exact same design we can fold it over.
We can fold it over on all factors, or specify a single factor for folding.
What folding means is to take the design and reverse the sign on all the factors. This would be a fold on all factors.
Now instead of eight observations, we have 16. And if you look at the first eight and compare these with the second set of eight you will see that the signs have simply been reversed.
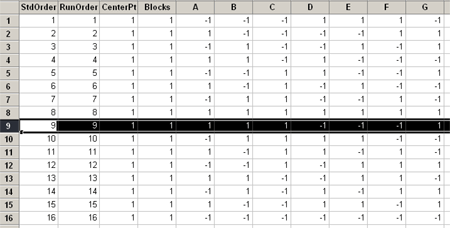
Look at row 1 and row 9 and you will see that they have the exact opposite signs. Thus you double the basic design with all factors exchanged. Or, you can think of this somewhat as taking one replicate and putting it in blocks, we've now taken two of the blocks to create our design.
These designs are used to learn how to proceed from a basic design, where you might have learned something about one of the factors that looks promising, and you want to give more attention to that factor. This would suggest folding, not on all factors, but folding on that one particular factor. Let's examine why you might want to do this.
In our first example above we started with a Resolution III design, and by folding it over on all factors, we have increased the resolution by one number, in this case it goes from resolution III to IV. So, instead of the main effects being confounded with two-way interactions, which they were before, now they are all clear of the two-way interactions. We still have the two-way interactions confounded with each other however.
Now, let's look at the situation where after the first run we were mostly intrigued by factor B.
Now, rather than fold on all factors we want to fold on just factor B.
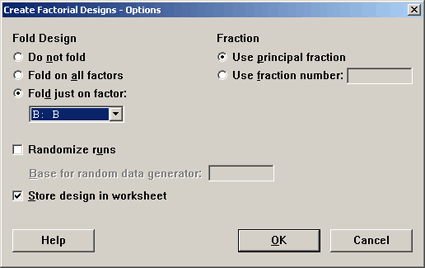
Notice now that in the column for B, the folded part is exactly the opposite. None of the other columns change, just the column for factor B. All of the other columns stayed the same.
Now look at the alias structure for this design...
Results for: Worksheet 8
| Factors: | 7 | Base Design: | 7, 8 | Resolution: | III |
| Runs: | 16 | Replicates: | 1 | Fraction: | 1/8 |
| Blocks: | 1 | Center pts (total): | 0 | ||
* NOTE * Some main effects are confounded with two-way interactions.
Design Generators: D = AB, E = AC, F = BC, G = ABC
Folded on Factors: B
Alias Structure
I + ACE + AFG + CDG + DEF + ACDF + ADEG + CEFG
A + CE + FG + CDF + DEG + ACDG + ADEF + ACEFG
B + ABCE + ABFG + BCDG + BDEF + ABCDF + ABDEG + BCEFG
C + AE + DG + ADF + EFG + ACFG + CDEF + ACDEG
D + CG + EF + ACF + ACDE + ADFG + CDEFG
E + AC + DF + ADG + CFG + AEFG + CDEG + ACDEF
F + AG + DE + ACD + CEG + ACEF + CDFG + ADEFG
AB + BCE + BFG + BCDF + BDEG + ABCDG + ABDEF + ABCEFG
AD + CF + EG + ACG + AEF + CDE + DFG + ACDEFG
BC + ABE + BDG + ABDF + BEFG + ABCFG + BCDEF + ABCDEG
BD + BCG + BEF + ABCF + ABEG + ABCDE + ABDFG + BCDEFG
BE + ABC + BDF + ABDG + BCFG + ABEFG + BCDEG + ABCDEF
BF + ABG + BDE + ABCD + BCEG + ABCEF + BCDFG + ABDEFG
BG + ABF + BCD + ABDE + BCEF + ABCEG + BDEFG + ABCDFG
ABD + BCF + BEG + ABCG + ABEF + BCDE + BDFG + ABCDEFG
This is still a Resolution III, (we haven't folded on all factors so we don't jump a resolution number). But look at the B factor which we folded. The main effect, B, is aliased with only the four way interactions and higher. Also, notice that all of the 2-way interactions with B are clear of other two-way interactions, so they become estimable. So by only folding on one factor, you get very good information on that factor and its interactions. However, it is still a resolution three design.
There are two purposes for folding; one is taking on another replicate for the purpose of moving to a higher resolution number. The other reason would be to isolate the information on a particular factor. Both of these would be done in the context of doing a sequential experiment, doing an analysis of that and then doing a second stage experiment. If you do this two-stage experiment, performing a second stage based on the first experiment, you should also use stage as the block factor in the analysis.
All of these designs, even though they are fractions of an experiment, should be blocked, if they are done in stages.
One more example ...
Let's go to 8 factors. The minimal design now cannot be eight observations but must be 16. This is a Resolution IV design.
Fractional Factorial Design
| Factors: | 8 | Base Design: | 8, 16 | Resolution: | IV |
| Runs: | 16 | Replicates: | 1 | Fraction: | 1/16 |
| Blocks: | 1 | Center pts (total): | 0 | ||
Design Generators: D = AB, E = AC, F = BC, G = ABC
Alias Structure (up to order 4)
I + ABCG + ABDH + ABEF + ACDF + ACEH + ADEG + AFGH + BCDE + BCFH + BDFG + BEGH + CDGH + CEFG + DEFH
A + BCG + BDH + BEF + CDF + CEH + DEG + FGH
B + ACG + ADH + AEF + CDE + CFH + DFG + EGH
C + ABG + ADF + AEH + BDE + BFH + DFG + EFG
D + ABH + ACF + AEG + BCE + BFG + CGH + EFH
E + ABF + ACH + ADG + BCD + BGH + CFG + DFH
F + ABE + ACD + AGH + BCH + BDG + CEG + DEH
G + ABC + ADE + AFH + BDF + BEH + CDH + CEF
H + ABD + ACE + AFG + BCF + BEG + CDG + DEF
AB + CG + DH + EF + ACDE + ACFH + ADFG + AEGH + BCDF + BCEH + BDEG + BFGH
AC + BG + DF + EH + ABDE + ABFH + ADGH + AEFG + BCDH + BCEF + CDEG + CFGH
AD + BH + CF + EG + ABCE + ABFG + ACGH + AEFH + BCDG + BDEF + CDEH + DFGH
AE + BF + CH + DG + ABCD + ABGH + ACFG + ADFH + BCEG + BDEH + CDEF + EFGH
AF + BE + CD + GH + ABCH + ABDG + ACEG + ADEH + BCFG + BDFH + CEFH + DEFG
AG + BC + DE + FH + ABDF + ABEH + ACDH + ACEF + BDGH + BEFG + CDFG + CEGH
AH + BD + CE + FG + ABCF + ABEG + ACDG + ADEF + BCGH + BEFH + CDFH + DEGH
This design has 4 generators BCDE, ACDF, ABCG and ABDH. It is a Resolution IV design and it is a design with16 observations. OK, now we are going to assume that we can only run these experiments eight at a time so we have to block. We will use two blocks, and we will still have the same fractional design, eight factors in 16 runs but now we want to have two blocks.
We let Minitab pick the blocks:
Fractional Factorial Design
| Factors: | 8 | Base Design: | 8, 16 | Resolution: | III |
| Runs: | 16 | Replicates: | 1 | Fraction: | 1/16 |
| Blocks: | 2 | Center pts (total): | 0 | ||
* NOTE * Blocks are confounded with two-way interactions.
Design Generators: E = BCD, F = ACD, G = ABC, H = ABD
Block Generators: AB
Alias Structure (up to order 4)
I + ABCG + ABDH + ABEF + ACDF + ACEH + ADEG + AFGH + BCDE + BCFH + BDFG + BEGH + CDGH + CEFG + DEFH
Blk = AB + CG + DH + EF + ACDE + ACFH + ADFG + AEGH + BCDF + BCEH + BDEG + BFGH
A + BCG + BDH + BEF + CDF + CEH + DEG + FGH
B + ACG + ADH + AEF + CDE + CFH + DFG + EGH
C + ABG + ADF + AEH + BDE + BFH + DGH + EFG
D + ABH + ACF + AEG + BCE + BFG + CGH + EFH
E + EBF + ACH + ADG + BCD + BGH + CFG + DFH
F + ABE + ACD + AGH + BCH + BDG + CEG + DEH
G + ABC + ADE + AFH + BDF + BEH + CDH + CEF
H + ABD + ACE + AFG + BCF + BEG + CDG + DEF
AC + GH + DF + EH + ABDE + ABFH + ADGH + AEFG + BCDH + BCEF + CDEG + CFGH
AD + GH + CF + EG + ABCE + ABFG + ACGH + AEFH + BCDG + BDEF + CDEH + DFGH
AE + BF + CH + DG + ABCD + ABGH + ACFG + ADFH + BCEG + BDEH + CDEF + EFGH
AF + BE + CD + GH + ABCH + ABDG + ACEG + ADEH + BCFG + BDFH + CEFH + DEFG
AG + BC + DE + FH + ABDF + ABEH + ACDH + ACEF + BDGH + BEFG + CDFG + CEGH
AH + BD + CE + FG + ABCF + ABEG + ACDG + ADEF + BCGH + BEFH + CDFH + DEGH
In this design, we have eight factors, 16 runs, and the same generators but now we need an additional generator, the block generator. Minitab is using AB as the block generator. Notice in the alias structure that the blocks are confounded with the AB term.
Notice also that the AB term does not show up as an estimable effect below. It would have been an effect we could have estimated but it is now confounded with blocks. So, one additional degree of freedom is used in this confounding with blocks.
The only choice the program had was to select one of these effects that were previously estimable and confound them with blocks. The program picked one of those 2-way interactions and this means blocks are now confounded with a 2-way interaction.
We can still block these fractional designs and it is useful to do this if you can only perform a certain number at a time. However, if you are doing sequential experimentation you should block just because you are doing it in stages.
In summary, when you fold over a Resolution III design on all factors, then you get a Resolution IV design. Look at the table of all possible designs in Minitab below:
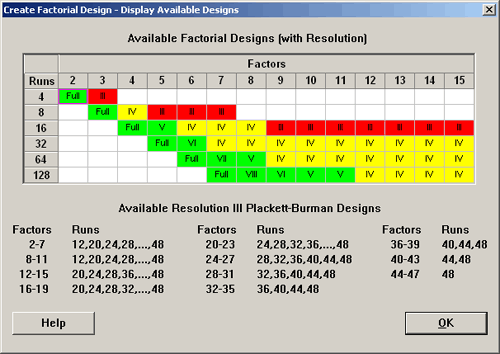
If you fold any of the red Resolution III designs you go to the next level, it has twice as many observations and becomes a Resolution IV design. If you fold many of the Resolution IV designs, even though you double the number of observations by folding, you are still at the Resolution IV.
Whereas, if you fold a Resolution III or IV design on one factor, you get better information on that factor and all its 2-way interactions would be clear of other 2-way interactions. Therefore, it serves that purpose well for Resolution III or IV designs.