options ls=78;
title "Profile Plot - Swiss Bank Notes";

 /* After reading in the swiss data, where each variable is
  * originally in its own column, the next statements stack the data
  * so that all variable names are in one column called 'variable',
  * and all response values minus their null values
  * are in another column called 'x'.
  * The subtraction is useful for plotting purposes because
  * it allows for a common reference value of 0 for all variables.
  */

data swiss;
  infile "D:\Statistics\STAT 505\data\swiss3.csv" firstobs=2 delimeter=',';
  input type $ length left right bottom top diag;
  variable="length"; x=length-215.0; output;
  variable="left  "; x=left-130.0;   output;
  variable="right "; x=right-130.0;  output;
  variable="bottom"; x=bottom-9.0;   output;
  variable="top   "; x=top-10.0;     output;
  variable="diag  "; x=diag-141.354; output;
  run;

proc sort;
  by type variable;
  run;

 /* The means procedure calculates and saves mean for
  * each variable and saves the results in a new data set 'a'
  * for use in the steps below.
  * /

proc means data=swiss;
  by type variable;
  var x;
  output out=a mean=xbar;
  run;

 /* The axis commands define the size of the plotting window.
  * The horizontal axis is of the variables, and the vertical
  * axis is used for the mean values.
  * /

proc gplot;
  axis1 length=4 in label=("Mean");
  axis2 length=6 in;
  plot xbar*variable=type / vaxis=axis1 haxis=axis2;
  symbol1 v=J f=special h=2 i=join color=black;
  symbol2 v=K f=special h=2 i=join color=black;
  run;

Analysis

The results are shown below:

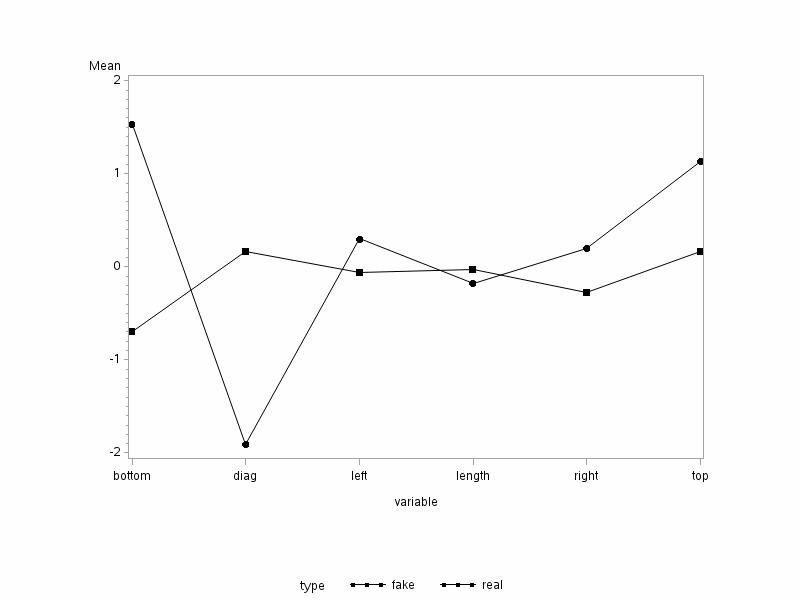
From this plot, we can see that the bottom and top margins of the counterfeit notes are larger than the corresponding mean for the genuine notes. Likewise, the left and right margins are also wider for the counterfeit notes than the genuine notes. However, the diagonal and length measurement for the counterfeit notes appears to be smaller than the genuine notes. Please note, however, this plot does not show which results are significant. The significance is from the previous simultaneous or Bonferroni confidence intervals.

One of the things to look for in these plots is if the line segments joining the dots are parallel to one another. In this case, they are not even close to being parallel for any pair of variables.

Profile Analysis

Profile Analysis is used to test the null hypothesis that these line segments are indeed parallel.  You should test the hypothesis that the line segments in the profile plot are parallel to one another only if the variables have the same units of measurement.  We might expect parallel segments if all of the measurements for the counterfeit notes are consistently larger than the measurements for the genuine notes by some constant.

Use the following procedure to test this null hypothesis:

Step 1: For each group, we create a new random vector \(Y_{ij}\) corresponding to the \(j^{th}\) observation from population i. The elements in this vector are the differences between the values of the successive variables as shown below:

\( \mathbf{Y}_{ij} = \left(\begin{array}{c}X_{ij2}-X_{ij1}\\X_{ij3}-X_{ij2}\\\vdots \\X_{ijp}-X_{ij,p-1}\end{array}\right)\)

Step 2: Apply the two-sample Hotelling's T-square to the data \(\mathbf{Y}_{ij}\) to test the null hypothesis that the means of the \(\mathbf{Y}_{ij}\)'s for population 1 are the same as the means of the \(\mathbf{Y}_{ij}\)'s for population 2:

\(H_0\colon \boldsymbol{\mu}_{\mathbf{Y}_1} = \boldsymbol{\mu}_{\mathbf{Y}_2}\)