Using SAS
To test for treatment by time interactions we need to carry out a Profile Analysis. We can create a Profile Plot as shown in the Dog SAS program. (This program is similar in structure to swiss13a.sas used in the Hotelling's T-square lesson previously.)
Here, we want to plot the treatment means against time for each of our four treatments. We can then examine the form the interactions take if they are deemed significant.
Download the SAS Program: dog1.sas
options ls=78;
title "Profile Plot - Dog Data";
data dogs;
infile "D:\Statistics\STAT 505\data\dog1.txt";
input treat dog p1 p2 p3 p4;
time=1; k=p1; output;
time=5; k=p2; output;
time=9; k=p3; output;
time=13; k=p4; output;
drop p1 p2 p3 p4;
run;
proc sort;
by treat time;
run;
proc means;
by treat time;
var k;
output out=a mean=mean;
filename t1 "dog.ps";
goptions device=ps300 gsfname=t1 gsfmode=replace;
proc gplot;
axis1 length=4 in;
axis2 length=6 in;
plot mean*time=treat / vaxis=axis1 haxis=axis2;
symbol1 v=J f=special h=2 i=join color=black;
symbol2 v=K f=special h=2 i=join color=black;
symbol3 v=L f=special h=2 i=join color=black;
symbol4 v=M f=special h=2 i=join color=black;
run;
This program plots the treatment means against time, separately for each treatment. Here, the means for treatment 1 are given by the circles, treatment 2 squares, treatment 3 triangles and treatment 4 stars.
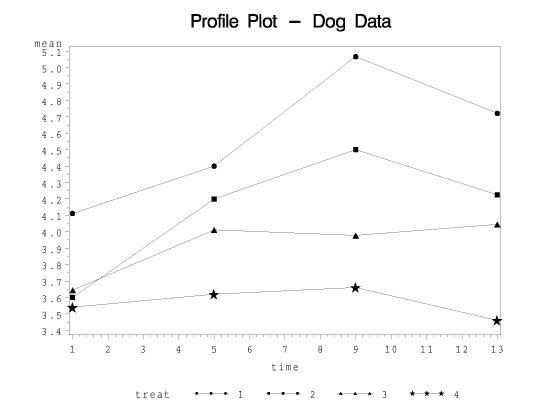
The test for interaction tests the hypothesis that these lines segments are parallel to one another.
To test for interaction, we define a new data vector for each observation. Here we consider the data vector for dog j receiving treatment i. This data vector is obtained by subtracting the data from time 2 minus the data from time 1, the data from time 3 minus the data from time 2, and so on...
This yields the vector of differences between successive times and is expressed as follows:
\(\mathbf{Z}_{ij} = \left(\begin{array}{c}Z_{ij1}\\ Z_{ij2} \\ \vdots \\ Z_{ij, t-1}\end{array}\right) = \left(\begin{array}{c}Y_{ij2}-Y_{ij1}\\ Y_{ij3}-Y_{ij2} \\ \vdots \\Y_{ijt}-Y_{ij,t-1}\end{array}\right)\)
Because this vector is a function of the random data, it is a random vector, and so has a population mean. Thus, for treatment i, we define the population mean vector \(E(\mathbf{Z}_{ij}) = \boldsymbol{\mu}_{Z_i}\).
Then we will perform a MANOVA on these \(Z_{ij}\)'s to test the null hypothesis that
\(H_0\colon \boldsymbol{\mu}_{Z_1} = \boldsymbol{\mu}_{Z_2} = \dots = \boldsymbol{\mu}_{Z_a} \)
Using SAS
The SAS program carries out this MANOVA procedure in the third MANOVA statement as highlighted below:
Download the SAS program: dog.sas
In the third manova statement, we are testing for interaction between treatment and time. We obtain the vector Z, by setting m equal to the differences between the data at different times. i.e., p2-p1, p3-p2, and p4-p3. This will carry out the profile analysis, or equivalently, test for interactions between treatment and time.
Let's look at the output. Again, be careful when you look at the results to make sure you are in the right part of the output.
| p1 | p2 | p3 | p4 | |
|---|---|---|---|---|
| MVAR1 | -1 | 1 | 0 | 0 |
| MVAR2 | 0 | -1 | 1 | 0 |
| MVAR3 | 0 | 0 | -1 | 1 |
Find the table with the kind of function used in defining the vector MVAR, comprised of the elements MVAR1, MVAR2, and MVAR3.
For MVAR1 we have minus p1 plus p2, for MVAR 2 we have minus p2 plus p3, and so on...
The results are then found below this table in the SAS output:
| Statistic | Value | F Value | Num DF | Den DF | Pr > F |
|---|---|---|---|---|---|
| Wilks' Lambda | 0.59835958 | 1.91 | 9 | 73.163 | 0.0637 |
| Pillai's Trace | 0.44352640 | 1.85 | 9 | 96 | 0.0689 |
| Hotelling-Lawley Trace | 0.60246548 | 1.96 | 9 | 44.068 | 0.0672 |
| Roy's Greatest Root | 0.46206108 | 4.93 | 3 | 32 | 0.0063 |
NOTE: F Statistic for Roy's Greatest Root is an upper bound.
Here we get a Wilks Lambda of 0.598 with a supporting F-value of 1.91 with 9 and 73 d.f.
This p-value is not significant if we strictly adhere to the 0.05 significance level.
Conclusion
There is weak evidence that the effect of treatment depends on time \( \left( \Lambda = 0.598; F = 1.91; d. f. = 9, 73; p = 0.0637 \right) \).
By reporting the p-value with our results, we allow the reader to make their own judgment regarding the significance of the test. Conservative readers might say that 0.0637 is not significant and categorically state that this is not significant, inferring that there is no evidence for interaction. More liberal readers, however, might say that this is very close and consider this weak evidence for an interaction. When you report the results in this form, including the p-value, you allow the reader to make their own judgment.