Confidence intervals for the Paired Hotelling's T-square are computed in the same way as for the one-sample Hotelling's T-square, therefore, the notes here will not be as detailed as for the one-sample. Let's review the basic procedures:
Simultaneous (1 - \(\alpha\)) × 100% Confidence Intervals for the mean differences are calculated using the expression below:
\(\bar{y}_j \pm \sqrt{\frac{p(n-1)}{n-p}F_{p,n-p,\alpha}}\sqrt{\frac{s^2_{Y_j}}{n}}\)
Bonferroni (1 - \(\alpha\)) × 100% Confidence Intervals for the mean differences are calculated using the following expression:
\(\bar{y}_j \pm t_{n-1, \frac{\alpha}{2p}}\sqrt{\frac{s^2_{Y_j}}{n}}\)
As before, simultaneous intervals will be used if we are potentially interested in confidence intervals for linear combinations among the variables of the data. Bonferroni intervals should be used if we want to simply focus on the means for each of the individual variables themselves. In this case, the individual questions.
Example 7-10: Spouse Data (Bonferroni CI) Section
Using SAS
The simultaneous Bonferroni Confidence intervals may be computed using the SAS program that can be downloaded below:
Download the Spouse 1 SAS Program: spouse1a.sas
In this output losim and upsim give the lower and upper bounds for the simultaneous intervals, and lobon and upbon give the lower and upper bounds for the Bonferroni interval which are copied into the table below. You should be able to find where all of these numbers are obtained.
Using Minitab
At this time Minitab does not support this procedure.
Analysis
|
95 % Confidence Intervals
|
||
|
Question
|
Simultaneous
|
Bonferroni
|
|
1
|
-0.5127, 0.6460
|
-0.3744, 0.5078
|
|
2
|
-0.7078, 0.4412
|
-0.5707, 0.3041
|
|
3
|
-0.7788, 0.1788
|
-0.6645, 0.0645
|
|
4
|
-0.6290, 0.3623
|
-0.5107, 0.2440
|
The simultaneous confidence intervals are plotted using Profile Plots.
Using SAS
The downloadable SAS program for the profile plot can be obtained here: spouse1.sas.
(Which in this case is analogous to the earlier SAS program Download here: nutrient6.sas)
Using Minitab
At this time Minitab does not support this procedure.
Analysis
Note: The plot is given in plot1 shown below:
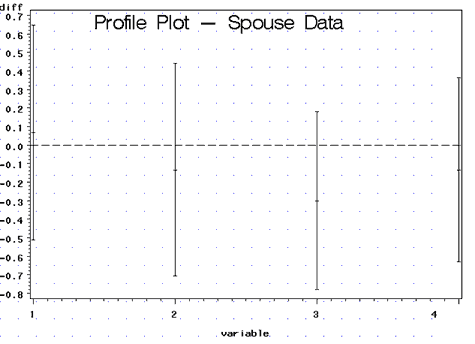
Here we can immediately notice that all of the simultaneous confidence intervals include 0 suggesting that the husbands and wives do not differ significantly in their responses to any of the questions. So what is going on here? Earlier the Hotelling's \(T^{2}\) test told us that there was a significant difference between the husband and wives in their responses to the questions. But the plot of the confidence intervals suggests that there are no differences.
Basically, the significant Hotelling's T-square result is achieved through the contributions from all of the variables. It turns out that there is going to be a linear combination of the population means of the form:
\[\Psi = \sum_{j=1}^{n}c_j\mu_{Y_j}\]
whose confidence interval will not include zero.
The profile plot suggests that the largest difference occurs in response to question 3. Here, the wives respond more positively than their husbands to the question: "What is the level of companionate love you feel for your partner?"