Common Procedures in Minitab

Common Procedures in Minitab

Quick Links

Quick Links

Calculate a T-Interval for a Population Mean

Calculate a T-Interval for a Population Mean

Minitab®

Procedure

A t-interval for a population mean provides an interval of estimates of the unknown population mean μ.

  1. Select Stat > Basic Statistics > 1 Sample t ...
  2. Use the pull-down options to select, 'Samples in columns.'
  3. Select the variable you want to analyze, (by double-clicking, or highlighting and clicking once on 'Select'.) so it appears in the box labeled 'Variables'.
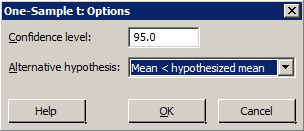
  4. Select 'Options' ... Type in the desired confidence level the default is 95.0 in the box labeled 'Confidence level'. (Ignore the box labeled 'Alternative'.) 
  5. Select OK.
  6. Select OK. The output will appear in the session window.

Example

The US National Research Council currently recommends that females between the ages of 11 and 50 intake 15 milligrams of iron daily.  The iron intakes of a random sample of 25 such American females are found in the dataset irondef.txt.  With 95% confidence, what is the mean iron intake of all American females?

Minitab Dialog Boxes

minitab dialog box for 1 sample t

minitab dialog box for one sample 1 options

Sample Minitab Output

One-Sample T: iron

Variable N Mean StDev SE Mean 95% CI
iron 25 14.300 2.367 0.473 (13.323, 15.277)

Video Review

Code Numeric to Numeric Data

Code Numeric to Numeric Data

Minitab®

Procedure

Minitab can be used to translate or "code" a column of numbers into another column of numbers. The procedure is particularly useful for creating dummy indicator variables for the qualitative predictor variables that you'd like to include in your regression model.

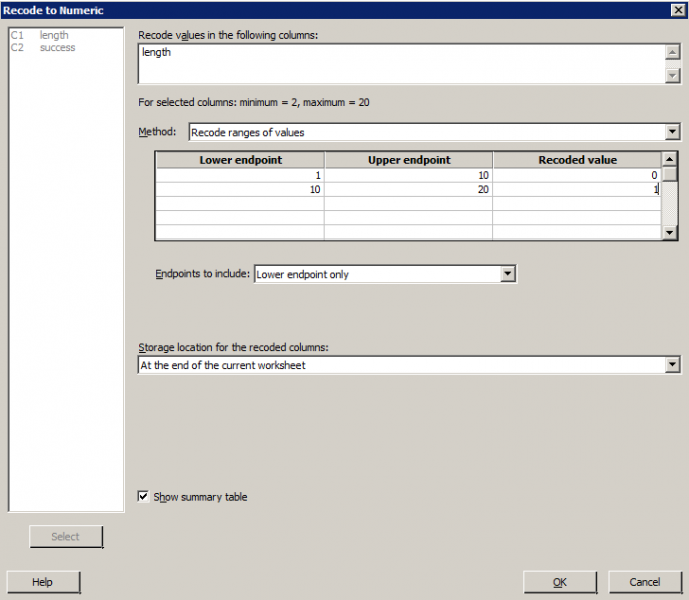
  1. In Minitab, select Data >> Recode >>  to Numeric...  
  2. In the box labeled Recode values in the following columns, specify the name of the numeric variable that you want to code.
  3. In the box labeled Method, specify a method for recoding the values specified above.
  4. For instance, to recode a range of values, type the numeric values in the boxes labeled Lower endpoint and Upper endpoint and the Recoded Value that you want this range to represent. Make sure you do this for every possible value of the variable that you want to code. 
  5. Select OK. The new variable should appear in your worksheet.

Note: if you have more than one numeric variable to create, you have to code each one separately.

Example

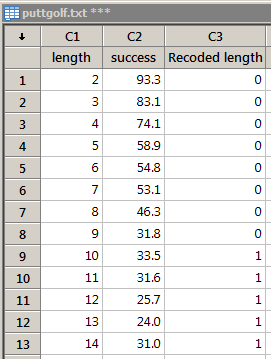
Sports Illustrated published results of a study designed to determine how well professional golfers putt. The data set puttgolf.txt contains data on the lengths of putts (x) and the percentage of successful putts (y) made by professional golfers during 15 tournaments. Only putts that were 2 to 20 feet from the hole are included in the data set. When fitting a two-piece piecewise linear regression function — connected at x = 10 — to the data, you have to create a new numeric dummy variable, say "dummy", that takes on value 0 if x ≤ 10 and 1 if x > 10. Use Minitab to code the numeric variable length into the numeric variable dummy.

Minitab Dialog Box

Minitab dialog box for coding numeric data to numeric

Resulting Minitab Worksheet

minitab worksheet

Video Review

Code a Text Variable into a Numeric Variable

Code a Text Variable into a Numeric Variable

Minitab®

Procedure

Minitab can be used to translate or "code" a column of text values into another column of numeric values.

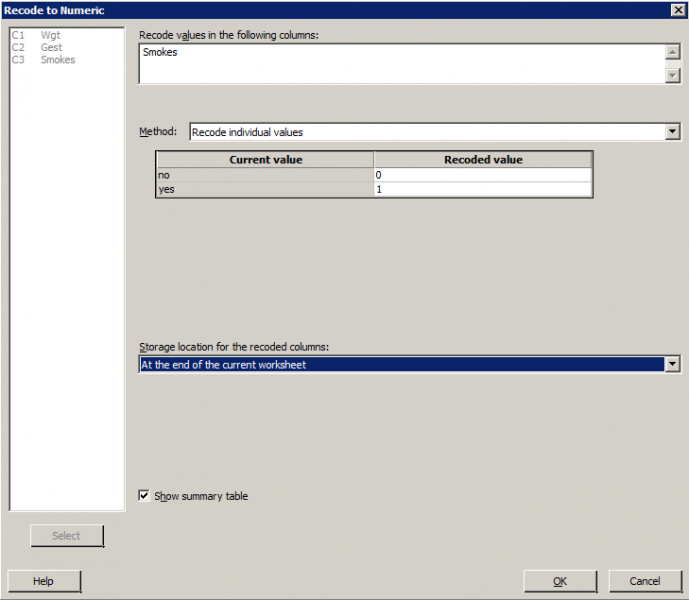
  1. In Minitab select Data >> Recode >> to Numeric... 
  2. In the box labeled Recode values in the following columns, specify the name of the text variable that you want to code.
  3. Under 'Method', select the option 'Recode individual values'.
  4. For each value of the variable that you want to code, type the text value in the box labeled Recoded value. Make sure you do this for every possible value of the text variable that you want to code.
  5. Select OK. The new numeric variable should appear in your worksheet.  You can rename the column in your worksheet with a more effective label if you want.

Note: if you have more than one text variable to create, you have to code each one separately.

Example

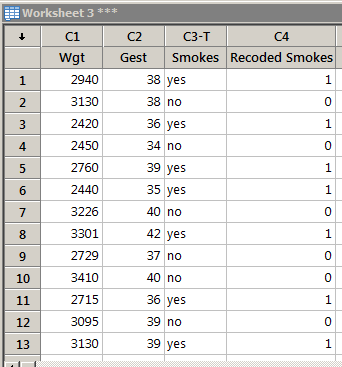
The data set birthsmokers2.txt contains data on the birthweight (y = Wgt), gestation length (x1 = Gest) and mother's smoking status (x2 = Smokes, yes or no) of babies born to 32 mothers. If you wanted to fit a multiple regression model that included smoking status, you'd first have to create a numeric variable in your worksheet, dummy say, that equals 1 if Smokes = yes and equals 0 if Smokes = no. Create the dummy variable in your worksheet.

Minitab Dialog Box

dialog box for coding text to numeric

Resulting Minitab Worksheet

worksheet

Video Review

Conduct Best Subsets Regression

Conduct Best Subsets Regression

Minitab®  – Procedure

  1. Select Stat >> Regression >> Best Subsets...
  2. In the box labeled Response, specify the response.
  3. In the box labeled Free predictors, specify the predictors that you want considered for the model. (Do not include predictors that you specify in the following Predictors in all models box.)
  4. (Optional) In the box labeled Predictors in all models, specify all of the predictors that must be included in every model considered.
  5. Select OK. The output will appear in the session window.

Example

Researchers were interested in learning how the composition of cement affected the heat evolved during the hardening of the cement. Therefore, they measured and recorded the following data (cement.txt) on 13 batches of cement:

  • Response y: heat evolved in calories during hardening of cement on a per gram basis
  • Predictor x1: % of tricalcium aluminate
  • Predictor x2: % of tricalcium silicate
  • Predictor x3: % of tetracalcium alumino ferrite
  • Predictor x4: % of dicalcium silicate

Perform a best subsets regression. In doing so, require that the predictor x2 be included in all models considered.

Minitab Dialog Box

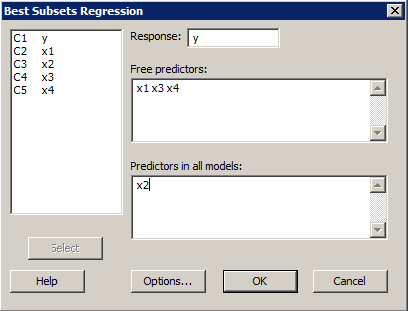
Minitab dialog box for best subsets regression

Sample Output

Best Subsets Regression: y versus x1, x3, x4, x2

Response is y
The following variables are included in all models:  x2

Vars              R-Sq Mallows   x x x
    R-Sq(adj)          Cp S 1 3 4
1 97.9 97.4 2.7     2.4063 x    
1 84.7 81.6 62.4 6.4455   x  
2 98.2 97.6 3.0 2.3087 x   x
2 98.2 97.6 3.0 2.3121 x x  
3 98.2 97.4 5.0 2.4460 x x x

Video Review

Conduct Regression Error Normality Tests

Conduct Regression Error Normality Tests

Minitab®  – Procedure

If you haven't already done so, store the residuals on which you want to conduct the Ryan Joiner correlation test.

  1. Select Stat > Regression > Regression > Fit Regression Model...
  2. Specify the response and the predictor variable(s).
  3. Select Storage... Under Diagnostic Measures, select the type of residuals (and/or influence measures) that you want to store. Select OK.
  4. Select OK. The requested residuals (and/or influence measures) will be stored in your worksheet.

Once Minitab has stored the residuals in your worksheet:

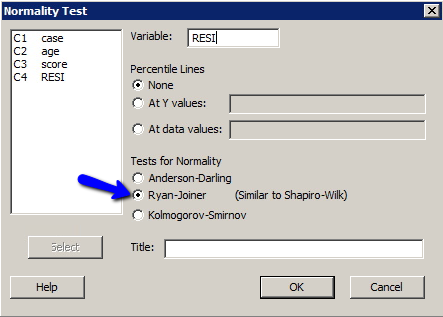
  1. Select Stat > Basic Statistics > Normality Test...
  2. In the box labeled Variable, specify the name of the variable containing the residuals (Minitab names it something like RESI1, RESI2, ...).
  3. Under Tests for Normality, select Anderson-Darling, Ryan-Joiner, or Kolmogorov-Smirnov.
  4. Select OK. A new graph window containing the requested normal probability plot should appear.

Example

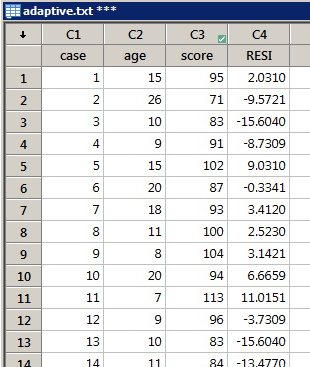
The data set adaptive.txt contains the Gesell adaptive scores and ages (in months) of n = 21 children with cyanotic heart disease. Upon regressing the response y = score on the predictor x = age, use the resulting residuals to test whether or not the error terms are normally distributed.

Minitab Dialog Boxes

Minitab regression dialog box

Minitab regression dialog box - storage

Minitab Normality test dialog box

Sample Output

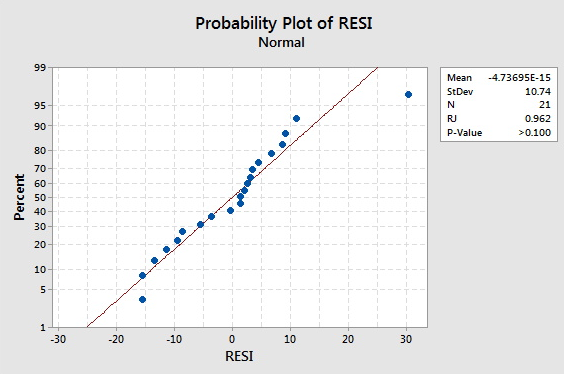
Probability Plot of RESI1

Video Review

Conduct Stepwise Regression

Conduct Stepwise Regression

Minitab®  – Procedure

  1. Select Stat >> Regression >> Regression >> Fit Regression Model...
  2. In the box labeled Response, specify the response.
  3. In the box labeled Continuous Predictors, specify all the predictors that you want to be considered for the model.
  4. Click on the Stepwise button.
  5. Choose 'Stepwise' from among the Method pull-down options.
  6. (Optional) Use the buttons below the box labeled Potential terms to indicate terms to include in every model, specify all of the predictors that must be included in every model considered.
  7. (Optional) Specify the Alpha to enter and Alpha to remove significance levels. The default for both is 0.15. 
  8. Check the box labeled 'Display the table of model selection details using the pull-down to select 'Include details for each step'.
  9. Select OK.
  10. Select OK. The output will appear in the session window.

Example

Researchers were interested in learning how the composition of cement affected the heat evolved during the hardening of the cement. Therefore, they measured and recorded the following data (cement.txt) on 13 batches of cement:

  • Response y: heat evolved in calories during hardening of cement on a per gram basis
  • Predictor x1: % of tricalcium aluminate
  • Predictor x2: % of tricalcium silicate
  • Predictor x3: % of tetracalcium alumino ferrite
  • Predictor x4: % of dicalcium silicate

Perform stepwise regression on the data set. Let αE = αR = 0.15. In doing so, require that the predictor x2 be included in all models considered.

Minitab Dialog Boxes

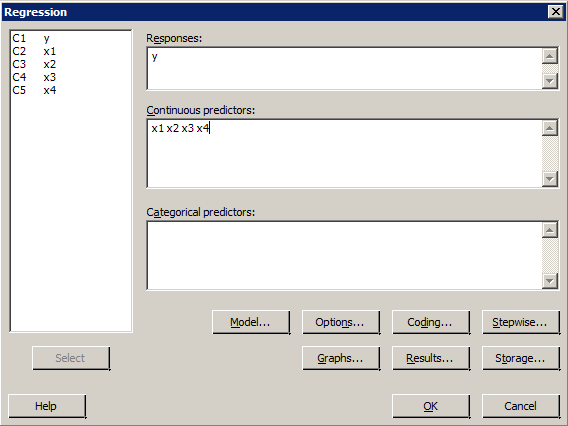
regression dialog box

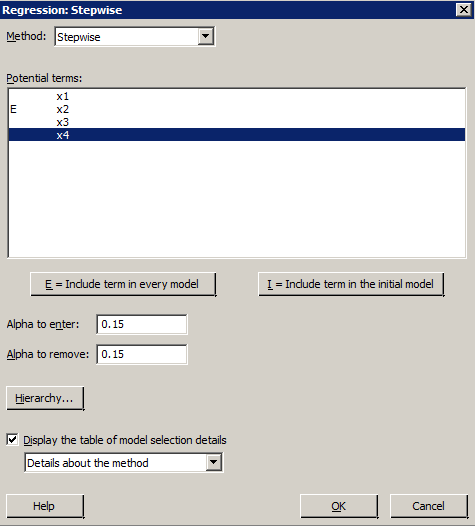
regression stepwise dialog box

Sample Output

Regression analysis: y versus x1, x2, x3, x4

Stepwise Selection of Terms
Candidate terms: x1, x2, x3, x4

Terms --------Step 1-------- --------Step 2--------
Coef      P    Coef P   
Constant 57.42   52.58  
x2 0.789 0.001 0.6623 0.000
x1     1.468 0.000
         
S   9.07713   2.40634
R-sq   66.63%   97.87%
R-sq(adj)   63.59%   97.44%
R-sq(pred)   55.74%   96.54%
Mallows' Cp   142.49   2.68

\(\alpha\) to enter = 0.15, \(\alpha\) to remove = 0.15 At your request, the stepwise procedure included these terms in every module: x2

Video Review

Conduct a Lack of Fit Test

Conduct a Lack of Fit Test

Minitab®

Procedure

  1. Select Stat >> Regression >> Regression ...  >> Fit Regression Model ... 
  2. Specify the response and the predictor(s).
  3. Minitab automatically recognizes replicates of data and produces the Lack of Fit test with Pure error by default.
  4. Select OK. The output will appear in the session window.

Example

The data set bluegills.txt contains the lengths (in mm) and ages (in years) of n = 78 bluegill fish. Is there sufficient evidence to conclude that there is a lack of linear fit between y = length and x = age of bluegill fish?

Minitab Dialog Box

Minitab 17 regression dialog box

Sample Output

Regression Analysis: length versus age

Analysis of Variance
Source DF   Adj SS Adj MS   F-value   P-value
Regression 1 32966    32965.8 210.66    0.000
     age 1 32966    32965.8 210.66    0.000
Error 76 11893 156.5    

     Lack-of-Fit

 4 3080

770.0

 6.29    0.000
     Pure Error 72 8813 122.4    
Total 77 44859      

Video Review

Conducting a Hypothesis Test for the Population Correlation Coefficient P

Conducting a Hypothesis Test for the Population Correlation Coefficient P

There is one more point we haven't stressed yet in our discussion about the correlation coefficient r and the coefficient of determination r2 — namely, the two measures summarize the strength of a linear relationship in samples only. If we obtained a different sample, we would obtain different correlations, different r2 values, and therefore potentially different conclusions. As always, we want to draw conclusions about populations, not just samples. To do so, we either have to conduct a hypothesis test or calculate a confidence interval. In this section, we learn how to conduct a hypothesis test for the population correlation coefficient ρ (the Greek letter "rho").

Incidentally, where does this topic fit in among the four regression analysis steps?

  • Model formulation
  • Model estimation
  • Model evaluation
  • Model use

It's a situation in which we use the model to answer a specific research question, namely whether or not a linear relationship exists between two quantitative variables

In general, a researcher should use the hypothesis test for the population correlation ρ to learn of a linear association between two variables, when it isn't obvious which variable should be regarded as the response. Let's clarify this point with examples of two different research questions.

We previously learned that to evaluate whether or not a linear relationship exists between skin cancer mortality and latitude, we can perform either of the following tests:

  • t-test for testing H0: β1= 0
  • ANOVA F-test for testing H0: β1= 0

That's because it is fairly obvious that latitude should be treated as the predictor variable and skin cancer mortality as the response. Suppose we want to evaluate whether or not a linear relationship exists between a husband's age and his wife's age? In this case, one could treat the husband's age as the response:

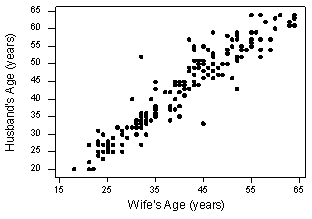
husband's age vs wife's age plot

Pearson correlation of HAge and WAge = 0.939

or one could treat wife's age as the response:

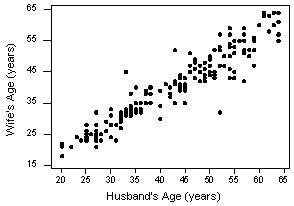
wife's age vs husband's age plot

Pearson correlation of HAge and WAge = 0.939

In cases such as these, we answer our research question concerning the existence of a linear relationship by using the t-test for testing the population correlation coefficient H0: ρ = 0.

Let's jump right to it! We follow standard hypothesis test procedures in conducting a hypothesis test for the population correlation coefficient ρ. First, we specify the null and alternative hypotheses:

Null hypothesis H0: ρ = 0
Alternative hypothesis HA: ρ ≠ 0 or HA: ρ < 0 or HA: ρ > 0

Second, we calculate the value of the test statistic using the following formula:

Test statistic:  \(t^*=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}\) 

Third, we use the resulting test statistic to calculate the P-value. As always, the P-value is the answer to the question "how likely is it that we’d get a test statistic t* as extreme as we did if the null hypothesis were true?" The P-value is determined by referring to a t-distribution with n-2 degrees of freedom.

Finally, we make a decision:

  • If the P-value is smaller than the significance level α, we reject the null hypothesis in favor of the alternative. We conclude "there is sufficient evidence at the α level to conclude that there is a linear relationship in the population between the predictor x and response y."
  • If the P-value is larger than the significance level α, we fail to reject the null hypothesis. We conclude "there is not enough evidence at the α level to conclude that there is a linear relationship in the population between the predictor x and response y."

Let's perform the hypothesis test on the husband's age and wife's age data in which the sample correlation based on n = 170 couples is r = 0.939. To test H0: ρ = 0 against the alternative HA: ρ ≠ 0, we obtain the following test statistic:

\[t^*=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}=\frac{0.939\sqrt{170-2}}{\sqrt{1-0.939^2}}=35.39\]

To obtain the P-value, we need to compare the test statistic to a t-distribution with 168 degrees of freedom (since 170 - 2 = 168). In particular, we need to find the probability that we'd observe a test statistic more extreme than 35.39, and then, since we're conducting a two-sided test, multiply the probability by 2. Minitab helps us out here:

Student's t distribution with 168 DF
x P ( X <= x )
35.3900 1.0000

The output tells us that the probability of getting a test statistic smaller than 35.39 is greater than 0.999. Therefore, the probability of getting a test statistic greater than 35.39 is less than 0.001. As illustrated in this , we multiply by 2 and determine that the P-value is less than 0.002. Since the P-value is small — smaller than 0.05, say — we can reject the null hypothesis. There is sufficient statistical evidence at the α = 0.05 level to conclude that there is a significant linear relationship between a husband's age and his wife's age.

Incidentally, we can let statistical software like Minitab do all of the dirty work for us. In doing so, Minitab reports:

Pearson correlation of WAge and HAge= 0.939
P-Value = 0.000

It should be noted that the three hypothesis tests we learned for testing the existence of a linear relationship — the t-test for H0: β1= 0, the ANOVA F-test for H0: β1= 0, and the t-test for H0: ρ = 0 — will always yield the same results. For example, if we treat the husband's age ("HAge") as the response and the wife's age ("WAge") as the predictor, each test yields a P-value of 0.000... < 0.001:

The regression equation is HAge= 3.59 + 0.967 WAge
170 cases used 48 cases contain missing values
Predictor Coef SE Coef T P
Constant 3.590 1.159 3.10 0.002
WAge 0.96670 0.02742 35.25 0.000
S = 4.069 R-Sq = 88.1% R-sq(adj) = 88.0%
Analysis of Variance
Source DF SS MS F P
Regression 1 20577 20577 1242.51 0.000
Error 168 2782 17    
Total 169 23359      
Pearson correlation of WAge and HAge = 0.939
P-Value = 0.000

And similarly, if we treat the wife's age ("WAge") as the response and the husband's age ("HAge") as the predictor, each test yields of P-value of 0.000... < 0.001:

The regression equation is WAge= 1.57 + 0.911 HAge
170 cases used 48 cases contain missing values
Predictor Coef SE Coef T P
Constant 1.574 1.150 1.37 0.173
WAge 0.91124 0.02585 35.25 0.000
S = 3.951 R-Sq = 88.1% R-sq(adj) = 88.0%
Analysis of Variance
Source DF SS MS F P
Regression 1 19396 19396 1242.51 0.000
Error 168 2623 17    
Total 169 22019      
Pearson correlation of WAge and HAge = 0.939
P-Value = 0.000

Technically, then, it doesn't matter what test you use to obtain the P-value. You will always get the same P-value. But, you should report the results of the test that make sense for your particular situation:

  • If one of the variables can be clearly identified as the response, report that you conducted a t-test or F-test results for testing H0: β1 = 0. (Does it make sense to use x to predict y?)
  • If it is not obvious which variable is the response, report that you conducted a t-test for testing H0: ρ = 0. (Does it only make sense to look for an association between x and y?)

One final note ... as always, we should clarify when it is okay to use the t-test for testing H0: ρ = 0? The guidelines are a straightforward extension of the "LINE" assumptions made for the simple linear regression model. It's okay:

  • When it is not obvious which variable is the response.
  • When the (x, y) pairs are a random sample from a bivariate normal population.
    • For each x, the y's are normal with equal variances.
    • For each y, the x's are normal with equal variances.
    • Either, y can be considered a linear function of x.
    • Or, x can be considered a linear function of y.
  • The (x, y) pairs are independent

Create Interaction Variables

Create Interaction Variables

Minitab®  – Procedure

In order to enter interaction terms into a regression model in Minitab, you have to first create column(s) in the worksheet that contains the interaction term(s).

  1. Select Calc >> Calculator...
  2. In the box labeled Store the result in variable, specify the column (or the name of the new variable, x1x2, for example) in which you want to store the interaction term.
  3. In the box labeled Expression, multiply the two predictor variables that go into the interaction terms. For example, if you want to create an interaction between x1 and x2, use the calculator to multiply them together: 'x1'*'x2'.
  4. Select OK. The new variable, x1x2, should appear in your worksheet.

Example

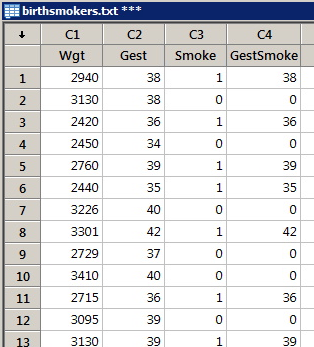
The data set birthsmokers.txt contains data on the birthweight (y = Wgt), gestation length (x1 = Gest) and (x2 = Smoke, 1 if mother smoked, 0 if not) of babies born to 32 mothers. If you wanted to fit a multiple regression model that allowed interaction between gestation length and smoking, you'd first have to create a variable in your worksheet, GestSmoke say, that contained the interaction term. Use Minitab's calculator to create the interaction term in your worksheet.

Minitab Dialog Box

Minitab calculator dialog box

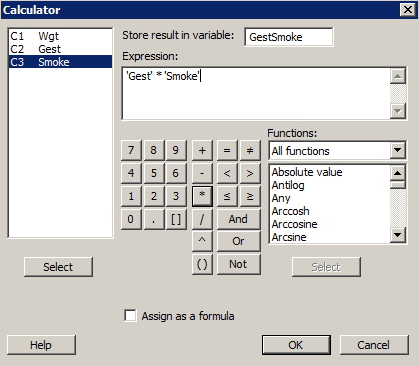
Sample of Resulting Minitab Worksheet

minitab worksheet

Video Review

Create Residual Plots

Create Residual Plots

Minitab®  – Procedure

  1. Select Stat >> Regression >> Regression ... >> Fit Regression Model ...
  2. Specify the response and the predictor(s).
  3. Under Graphs...
    1. Under Residuals for Plots, select either Regular or Standardized.
    2. Under Residuals Plots, select the desired types of residual plots. If you want to create residuals vs. predictor plot, specify the predictor variable in the box labeled Residuals versus the variables.
    3. Select OK.
  4. Select OK. The standard regression output will appear in the session window, and the residual plots will appear in new windows.

Example

The data set bluegills.txt contains the lengths (in mm) and ages (in years) of n = 78 bluegill fish. Treating y = length as the response and x = age as the predictor, request a normal plot of the standardized residuals and a standardized residuals vs. fits plot.

Minitab dialog boxes

Minitab regression dialog box

Minitab regression: graphs dialog box

Sample output

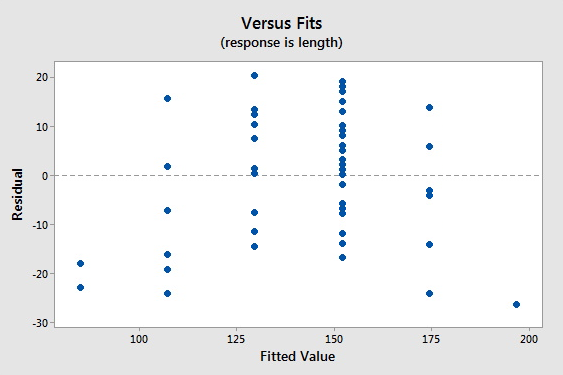
residuals vs fitted values plot

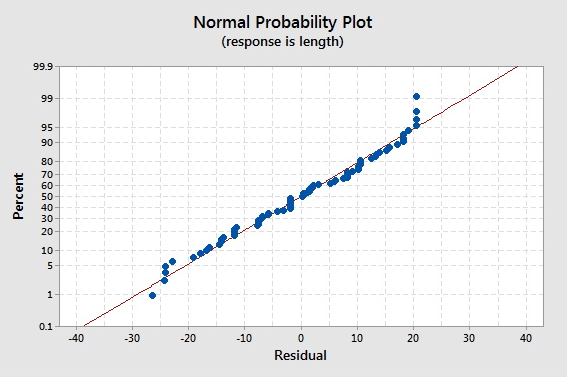
normal probability plot of the residuals

Video Review

Create a Basic Scatter Plot

Create a Basic Scatter Plot

Minitab®  – Procedure

The basic "scatter plot" command creates a simple scatter plot of a response variable y against a predictor variable x.

  1. Select Graph >> Scatterplot ...
  2. Select the graph type "Simple."
  3. Specify your Y variable and your X variable in the boxes provided.
  4. Select OK. A new window containing the scatter plot will appear.

Example

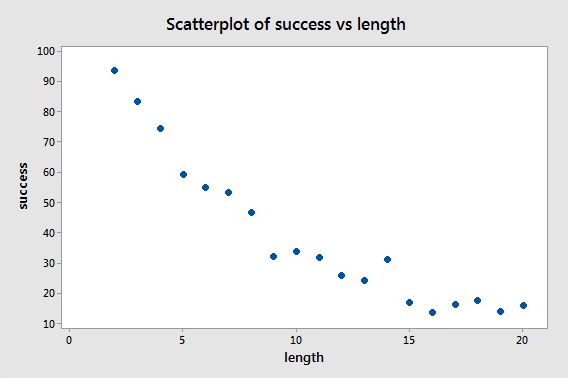
Sports Illustrated published results of a study designed to determine how well professional golfers putt. The data set puttgolf.txt contains data on the lengths of putts and the percentage of successful putts made by professional golfers during 15 tournaments. Only putts that were 2 to 20 feet from the hole are included in the data set.

What do the plot of y = success and x = length suggest about the relationship between the two variables?

Minitab Dialog Box

Minitab simple scatterplot dialog box

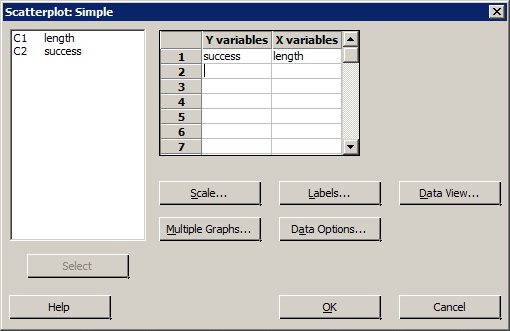
Minitab Sample Plot

minitab output of scatterplot

Video Review

Create a Fitted Line Plot

Create a Fitted Line Plot

Minitab®  – Procedure

The "fitted line plot" command is one way of obtaining the estimated regression function between a response y and a predictor x. The "fitted line plot" command provides not only the estimated regression function but also a scatter plot of the data adorned with the estimated regression function.

  1. Select Stat >> Regression >> Fitted Line Plot...
  2. In the box labeled "Response (Y)", specify the desired response variable.
  3. In the box labeled "Predictor (X)", specify the desired predictor variable.
  4. Select OK. A new window containing the fitted line plot will appear.

Example

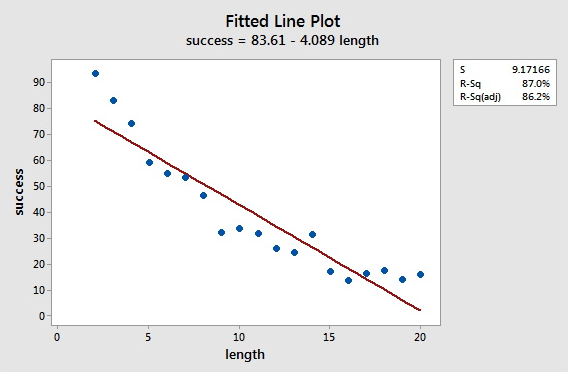
Sports Illustrated published results of a study designed to determine how well professional golfers putt. The data set puttgolf.txt contains data on the lengths of putts and the percentage of successful putts made by professional golfers during 15 tournaments. Only putts that were 2 to 20 feet from the hole are included in the data set.

What is the estimated linear relationship between y = success and x = length?

Minitab Dialog Box

Minitab fitted line plot dialog box

Sample Output

minitab output - fitted line plot

Video Review

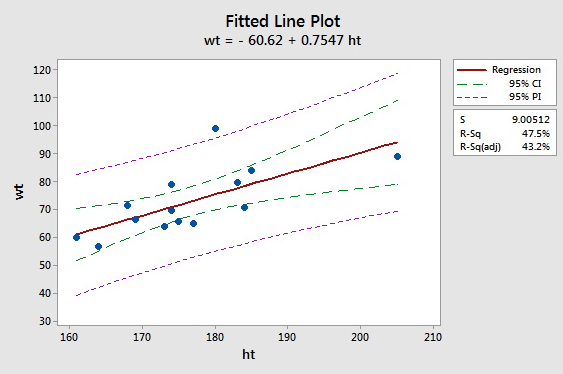
Create a Fitted Line Plot with Confidence and Prediction Bands

Create a Fitted Line Plot with Confidence and Prediction Bands

Minitab®  – Procedure

  1. Select Stat >> Regression >> Fitted line plot...
  2. Specify the response and the predictor.
  3. Select Options... Under Display Options, select Display confidence interval and select Display prediction interval. Specify the desired confidence level — 95% is the default. Select OK.
  4. Select OK. A new window containing the fitted line plot will appear.

Example

For people of the same age and gender, height is often considered a good predictor of weight. The data set htwtmales.txt contains the heights (ht, in cm) and weights (wt, in kg) of a sample of 14 males between the ages of 19 and 26 years.

  1. Find a 95% prediction band for the weight of a randomly selected male, aged 19 to 26.
  2. Find a 95% confidence band for the average weight of all males, aged 19 to 26.

Minitab Dialog Boxes

minitab fitted line plot dialog box

minitab fitted line plot - options dialog box

Sample Minitab Output Plot

minitab fitted line plot

Video Review

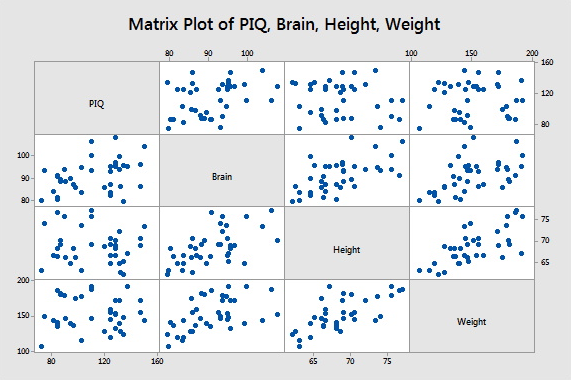
Create a Simple Matrix of Scatter Plots

Create a Simple Matrix of Scatter Plots

Minitab®  – Procedure

Creating a matrix of scatter plots between a set of variables is a good way to visualize the relationship between each pair of variables.

  1. Select Graph >> Matrix plot...
  2.  Under Matrix of plots, select the Simple plot.
  3. In the box labeled Graph variables, specify the variables you want to include in your plot.
  4. Select OK. A new graph window should appear containing the scatter plot matrix.

Example

Using the dataset iqsize.txt, create a matrix of scatter plots between each pair of the four variables.

Minitab dialog boxes

Minitab dialog box for matrix plots

Minitab dialog box for matrix plots

Resulting scatter plot matrix

Minitab output

Video Review

Creating a Correlation Matrix

Creating a Correlation Matrix

Minitab®  – Procedure (v.16 & v.17)

  1. Select Stat >> Basic statistics >> Correlation...
  2. In the box labeled Variables, specify the two (or more) variables for which you want the correlation coefficient(s) calculated.
  3. If you would like a P-value so that you can test that each population correlation is 0, put a checkmark in the box labeled Display p-values by clicking once on the box.
  4. Select OK. The output will appear in the session window.

Example

Using the iqsize.txt data set, estimate the correlations among each pair of the four variables.

Minitab Dialog Box

minitab dialog box for correlation

Resulting Minitab Output

Correlations: PIQ, Brain, Height, Weight

PIQ     Brain Height
Brain 0.378    
0.019    
     
Height -0.093 0.588  
0.578 0.000  
     
Weight 0.003 0.513 0.700
0.988 0.001 0.000
     
Cell Contents: Pearson correlation
                          P-Value

Display Data

Display Data

Minitab®  – Procedure

  1. In Minitab, select Data >> Display Data...
  2. In the box labeled Columns, constants, and matrices to display, specify the variables that you would like displayed.
  3. Select OK. The data will be displayed in the session window.

Example

Display the data contained in the adaptive.txt data set.

Minitab dialog box

Minitab dialog box for displaying data

Sample output

Results for: Worksheet 2
Data Display

Row case age score
1 1 15 95
2 2 26 71
3 3 10 83
4 4 9 91
5 5 15 102
6 6 20 87
7 7 18 93
8 8 11 100
9 9 8 104
10 10 20 94
11 11 7 113
12 12 9 96
13 13 10 83
14 14 11 84
15 15 11 102
16 16 10 100
17 17 12 105
18 18 42 57
19 19 17 121
20 20 11 86
21 21 10 100

Video Review

Find a Confidence Interval and a Prediction Interval for the Response

Find a Confidence Interval and a Prediction Interval for the Response

Minitab®  – Procedure

  1. Select Stat >> Regression >> Regression >> Fit Regression Model ...
  2. Specify the response and the predictor(s).
  3. Select OK. The output will appear in the session window.

Next, back up to the Main Menu having just run this regression:

  1. Select Stat >> Regression >> Regression >> Predict ...
  2. Specify the response.
  3. Specify either the x value ("Enter individual values") or a column name ("Enter columns of values") containing multiple x values.
  4. Select Options...  Specify the Confidence level — the default is 95%. Select OK.
  5. Select OK. The output will appear in the session window.

Example

For people of the same age and gender, height is often considered a good predictor of weight. The data set htwtmales.txt contains the heights (ht, in cm) and weights (wt, in kg) of a sample of 14 males between the ages of 19 and 26 years.

  1. Find a 95% prediction interval for the weight of a randomly selected male, aged 19 to 26, who is 170 centimeters tall.
  2. Find a 95% confidence interval for the average weight of all males, aged 19 to 26, who are 170 centimeters tall.

Minitab Dialog Boxes

Minitab regression dialog box

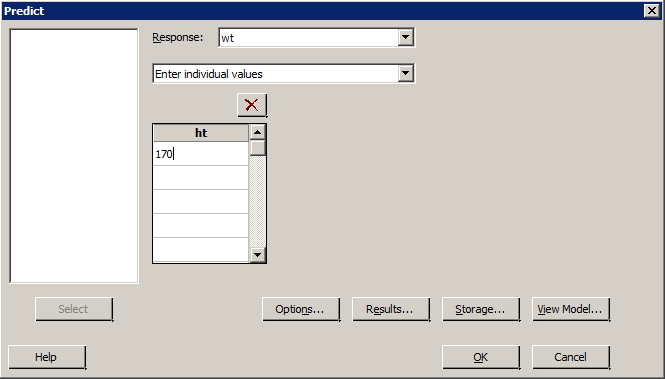
Minitab regression prediction dialog box

Resulting Sample Minitab Output

Prediction for wt

Regression Equation

wt = -60.6 + 0.755 ht
 

Variable Setting no heading no heading
ht 170  
 
Fit SE Fit 95% CI 95%PI
67.6694 2.83819 (61.4855, 73.8533) (47.0975, 88.2413)

Video Review

Find a t Critical Value

Find a t Critical Value

Minitab®  – Procedure

You may need to find a t critical value if you are using the critical value approach to conduct a hypothesis test that uses a t-statistic.

  1. Select Calc >> Probability Distributions >> t ...
  2. Click the button labeled 'Inverse cumulative probability'. (Ignore the box labeled 'Noncentrality parameter'. That is, leave the default value of 0 as is.)
  3. Type in the number of degrees of freedom in the box labeled 'Degrees of Freedom'.
  4. Click the button labeled 'Input Constant'. In the box, type the cumulative probability for which you want to find the associated t-value.
  5. Select OK. The t-value will appear in the session window.

Example

The US National Research Council currently recommends that females between the ages of 11 and 50 intake 15 milligrams of iron daily.

Is there evidence that the population of American females is, on average, getting less than the recommended 15 mg of iron? That is, should we reject the null hypothesis H0: μ = 15 against the alternative HA: μ < 15?

The iron intakes (irondef.txt) of a random sample of 25 such American females yielded a t-statistic of -1.48.

If we were interested in calculating the test at the α = 0.05 level, what is the appropriate t-critical value to which we should compare the t-statistic?

Minitab Dialog Box

minitab t distribution dialog box

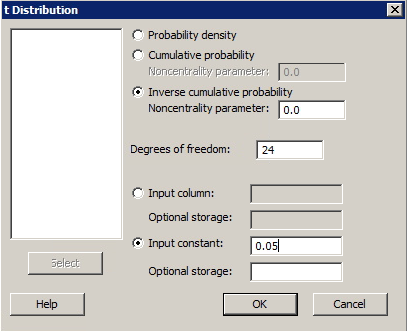
Sample Minitab Output

Inverse Cumulative Distribution Function

Student's t distribution with 24 DF

P ( X ≤ x)  x
0.05 -1.71088

Video Review

Find a t-based P-value

Find a t-based P-value

Minitab®  – Procedure

You may need to find a P-value if you are using the P-value approach to conduct a hypothesis test that uses a t-statistic.

  1. Select Calc >> Probability Distributions >> t ...
  2. Click the button labeled 'Cumulative probability'.
  3. Type the number of degrees of freedom in the box labeled 'Degrees of freedom'.
  4. Click the button labeled 'Input constant'. In the box, type the test statistic for which you want to find the associated cumulative probability.
  5. Select OK. The probability that a t-distributed random variable with this number of degrees of freedom is less than or equal to the test statistic will appear in the session window.
  6. The P-value is this probability for a lower-tail test or one minus this probability for an upper-tail test. For a two-tail test multiply the one-tail probability by two.

Example

The US National Research Council currently recommends that females between the ages of 11 and 50 intake 15 milligrams of iron daily.

Is there evidence that the population of American females is, on average, getting less than the recommended 15 mg of iron? That is, should we reject the null hypothesis H0: μ = 15 against the alternative HA: μ < 15?

The iron intakes (irondef.txt) of a random sample of 25 such American females yielded a t-statistic of -1.48.

If we were interested in calculating the test at the α = 0.05 level, what is the appropriate P-value to which we should compare the t-statistic?

Minitab Dialog Box

minitab t distribution dialog box

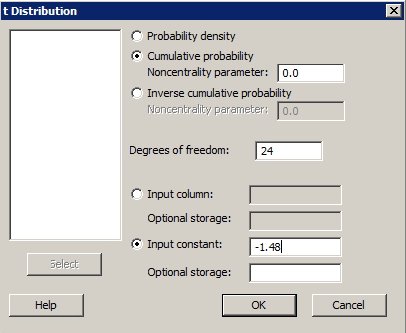
Sample Minitab Output

Cumulative Distribution Function

Student's t distribution with 24 DF

x P ( X ≤ x)
-1.48 0.0759408

Video Review

Find an F Critical Value

Find an F Critical Value

Minitab®  – Procedure

You may need to find an F critical value if you are using the critical value approach to conduct a hypothesis test that uses an F-statistic.

  1. Select Calc >> Probability Distributions >> F...
  2. Click the button labeled Inverse cumulative probability. (Ignore the box labeled Noncentrality parameter. That is, leave the default value of 0.0 as is.)
  3. Type in the number of numerator degrees of freedom in the box labeled Numerator degrees of freedom.
  4. Type in the number of denominator degrees of freedom in the box labeled Denominator degrees of freedom.
  5. Click the button labeled Input Constant. In the box, type the cumulative probability for which you want to find the associated F-value.
  6. Select OK. The F-value will appear in the session window.

Example

Some researchers at UCLA conducted a study on cyanotic heart disease in children. They measured the age at which the child spoke his or her first word (x, in months) and the Gesell adaptive score (y) on a sample of 21 children.

Is there evidence of a relationship between age at first word and Gesell adaptive score? That is, should we reject the null hypothesis H0: β1 = 0 against the alternative hypothesis HA: β1 ≠ 0 at the 0.05 level? The resulting data (adaptive.txt) yield an ANOVA F-statistic of 13.20.

Minitab Dialog Box

Because the F-test is large regardless of whether the population slope is positive or negative, the F-test is always a one-sided test. Therefore, because we want to conduct the hypothesis test at the 0.05 level, the appropriate cumulative probability to enter is 0.95. The number of numerator degrees of freedom is always 1 for a simple linear regression model with one predictor. Because there are 21 measurements in the sample, the appropriate number of denominator degrees of freedom is 19. Therefore, your Minitab dialog box should look like:

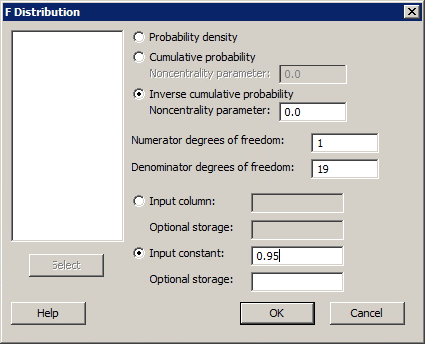
minitab F distribution dialog box

Sample Minitab Output

In this case, Minitab tells us that the F-critical value is:

Inverse Cumulative Distribution Function

F distribution with 1 DF in numerator and 19 DF in denominator

P ( X ≤ x)  x
0.95 4.38075

Video Review

Find an F-based P-value

Find an F-based P-value

Minitab®  – Procedure

You may need to find a P-value if you are using the P-value approach to conduct a hypothesis test that uses an F-statistic.

  1. Select Calc >> Probability Distributions >> F ...
  2. Click the button labeled Cumulative probability. (Leave the non centrality parameter set as the default of 0.)
  3. Type the number of numerator degrees of freedom in the box labeled Numerator degrees of freedom, and type the number of the denominator degrees of freedom in the box labeled Denominator degrees of freedom.
  4. Click the button labeled Input constant. In the box, type the value of your F-statistic for which you want to find the associated cumulative probability.
  5. Select OK. The cumulative probability will appear in the session window. The P-value is 1 minus the reported cumulative probability.

Example

The coolhearts.txt data set contains the following data on 32 rabbits subjected to a heart attack:

  • yi is the size of the infarcted area (in grams) of rabbit i
  • xi1 is the size of the region at risk (in grams) of rabbit i
  • xi2 = 1 if early cooling of rabbit i, 0 if not
  • xi3 = 1 if late cooling of rabbit i, 0 if not

It can be shown that the partial F-statistic for testing H0 : β2 = β3 = 0 is 8.59 with 2 numerator and 28 denominator degrees of freedom. Find the F-based P-value so that you can draw a conclusion about the hypothesis.

Minitab Dialog Box

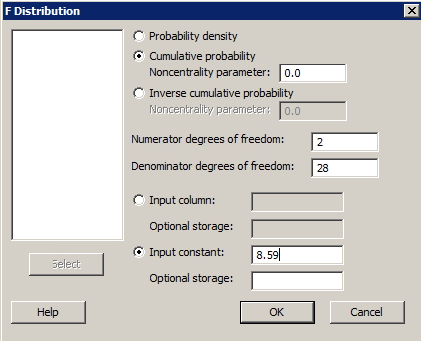
Minitab dialog box for F distribution

Sample Minitab Output

Cumulative Distribution Function

F distribution with 1 DF in numerator and 28 DF in denominator

x P ( X ≤ x)
8.59 0.998767

The P-value is therefore 1 - 0.9988 or 0.0012.

Video Review

Generate Random Normally Distributed Data

Generate Random Normally Distributed Data

Minitab®  – Procedure

Minitab can be used to generate random data. In this example, we use Minitab to create a random set of data that is normally distributed.

  1. Select Calc >> Random Data >> Normal...
  2. In the box labeled Generate ... rows of data, type in the number of rows of data that you would like to generate.
  3. In the box labeled Store in Column(s):, enter the column name(s) where you want Minitab to store the data.
  4. In the boxes labeled Mean: and Standard deviation: type in the mean and standard deviation of your desired normal distribution. The default is the standard normal distribution with mean = 0 and standard deviation = 1.
  5. Select OK. The new data will appear in the worksheet window.

Example

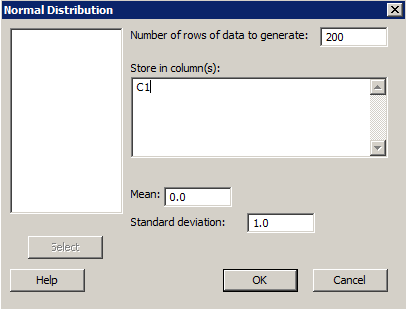
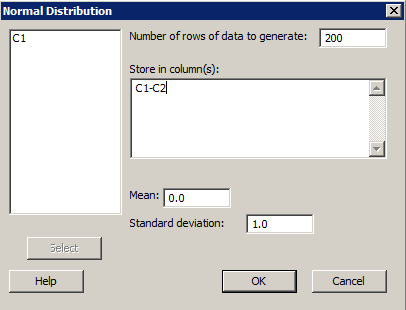
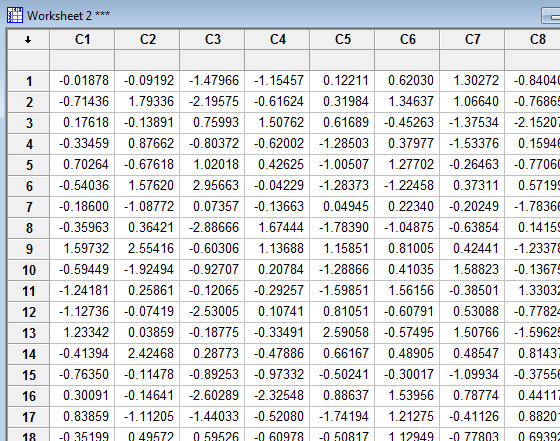
First, generate a column of 200 random numbers from a standard normal distribution with a mean of 0 and a standard deviation of 1. Then, generate 20 more columns, each containing 200 random numbers from a standard normal distribution with a mean of 0 and a standard deviation of 1.

Minitab Dialog Boxes

First option - one column:

normal distribution dialog box

Second method - multiple columns:

normal distribution dialog box

Resulting Minitab Worksheet

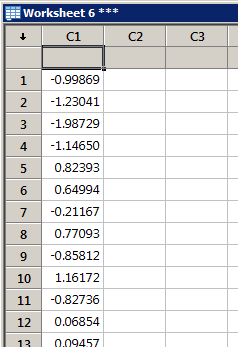
Based on the first dialog box above, one column (C1) of (standard) normally distributed data appears in the worksheet:

Minitab output...

Results based on specifying 20 columns (C1-C20) of (standard) normally distributed data as it will appear in the worksheet:

Minitab output

Video Review

 

Obtain a Sample Correlation

Obtain a Sample Correlation

Minitab®  – Procedure

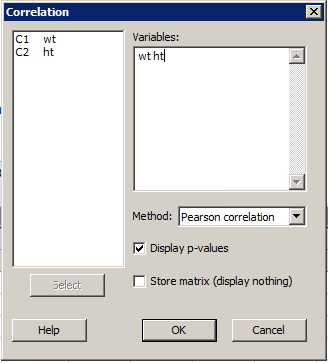
  1. Select Stat >> Basic statistics >> Correlation ...
  2. Specify the two (or more) variables for which you want the correlation coefficient(s) calculated.
    • Pearson correlation is the default.  An optional Spearman rho method is also available. 
  3. If it isn't already checked, put a checkmark in the box labeled Display p-values by clicking once on the box.
  4. Select OK. The output will appear in the session window.

Example

For people of the same age and gender, height is often considered a good predictor of weight. The data set htwtmales.txt contains the heights (ht, in cm) and weights (wt, in kg) of a sample of 14 males between the ages of 19 and 26 years.

  1. What is the sample correlation coefficient between ht and wt?
  2. Is there sufficient evidence to conclude that the population correlation coefficient between ht and wt is significantly different from 0?

Minitab Dialog Box

minitab correlation dialog box

Resulting Sample Minitab Output

Correlation: wt, ht

Pearson correlation of wt and ht = 0.689
P-Value = 0.006

Video Review

Perform a Basic Regression Analysis

Perform a Basic Regression Analysis

Minitab®  – Procedure

The "basic regression analysis" command outputs:

  • the estimated regression function
  • a table of estimated coefficients (Coef), which also includes standard errors of the coefficients (SE Coef), and t-statistics (T) and P-values (P) for testing the parameters differ from 0
  • the coefficient of determination r2
  • the analysis of variance table
  • a table of unusual observations
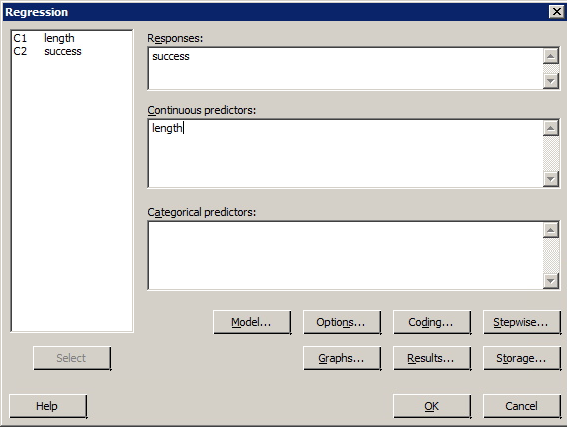
  1. Select Stat >> Regression >> Regression >> Fit Regression Model ... 
  2. In the box labeled "Response", specify the desired response variable.
  3. In the box labeled "Predictors", specify the desired predictor variable.
  4. Select OK. The basic regression analysis output will be displayed in the session window.

Regression Through the Origin

To fit an RTO model click "Model" in the regular regression window and uncheck "Include the constant term in the model".

Example

Sports Illustrated published results of a study designed to determine how well professional golfers putt. The data set puttgolf.txt contains data on the lengths of putts and the percentage of successful putts made by professional golfers during 15 tournaments. Only putts that were 2 to 20 feet from the hole are included in the data set.

Is there a significant linear relationship between the response y = success and the predictor x = length?

Minitab Basic Regression Analysis Dialog Box

Minitab regression dialog box

Sample Output

Regression Analysis: success versus length

Analysis of Variance
Source DF Adj SS Adj MS F-Value P-Value
Regression 1 9529 9529.29 113.28 0.000
length 1 9529 9529.29 113.28 0.000
Error 17 1430 84.12    
Total 18 10959      
Model Summary
S R-sq R-sq (adj) R-sq(pred)
9.17166 86.95% 86.18% 82.51%

Regression Equation

success = 83.61 - 4.089 length
Fits and Diagnostics for Unusual Observations
Obs success Fit Resid Std
Resid		 R
1 93.30 75.43 17.87 2.17
R Large residual

Video Review

Perform a Linear Regression Analysis

Perform a Linear Regression Analysis

Minitab®

  1. Select Stat >> Regression >> Regression >> Fit Regression Model ...
  2. Specify the response and the predictor(s).
  3. (For standard residual plots) Under Graphs..., select the desired residual plots.
  4. Minitab automatically recognizes replicates of data and produces the Lack of Fit test with Pure error by default.
  5.  Select OK.

Next, back up to the Main Menu having just run this regression:

  1. (To get a prediction interval) Select Stat >> Regression >> Regression >> Predict ...
  2. Specify the response.
  3. Specify either the x value ("Enter individual values") or a column name ("Enter columns of values") containing multiple x values.
  4. Select Options...  Specify the Confidence level — the default is 95%.  Select OK.
  5. Select OK. The output will be displayed in the session window.

Regression Through the Origin

To fit an RTO model click "Model" and uncheck "Include the constant term in the model".

Example

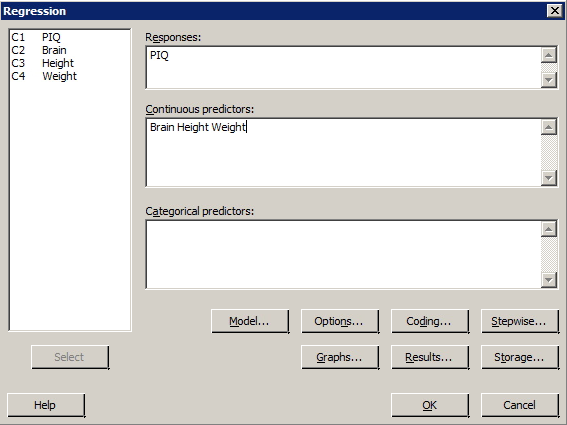
The iqsize.txt data set contains data on the IQ (y = PIQ), brain size (x1 = Brain), height (x2 = Height), and weight (x3 = Weight) of n = 38 college students. Fit the multiple linear regression model treating PIQ as the response, and Brain, Height, and Weight as the predictors. In doing so, request a lack of fit test. Also, with 95% confidence, predict the PIQ of a randomly selected college student whose Brain = 90, Height = 70 and Weight = 150.

Minitab Dialog Boxes

Minitab regression dialog box

Minitab regression predict dialog box

Resulting Minitab Output

Regression Analysis: PIQ versus Brain, Height, Weight

Analysis of Variance
Source DF Adj SS Adj MS F-Value P-Value
Regression 3 5572.7 1857.58 4.74 0.007
Brain 1 5239.2 5239.23 13.37 0.001
Height 1 1934.7 1934.71 4.94 0.033
Weight 1 0.0 0.0 0.00 0.998
Error 34 13321.8 391.82    
Total 37 18894.6      
Model Summary
S R-sq R-sq (adj) R-sq(pred)
19.7944 29.49% 23.27% 12.76%
Coefficients
Term Coef SE Coef T-Value P-Value VIF
Constant 111.4 63.0 1.77 0.086  
Brain 2.060 0.563 3.66 0.001 1.58
Height -2.73 1.23 -2.22 0.033 2.28
Weight 0.001 0.197 0.00 0.998 2.02

Regression Equation

PIQ = 111.4 + 2.060 Brain - 2.73 Height + 0.001 Weight
Fits and Diagnostics for Unusual Observations
Obs PIQ Fit Resid Std
Resid		 R
13 147.00 95.31 51.69 2.72
R Large residual
Prediction for PIQ

Regression Equation

PIQ = 111.4 + 2.060 Brain - 2.73 Height + 0.001 Weight
Variable Setting no heading
Brain 90        
Height 70        
Fit SE Fit 95% CI 95% PI
105.636 3.90554 (97.6986, 113.573) (64.6330, 146.638)

Video Review

Perform a t-test for a Population Mean µ

Perform a t-test for a Population Mean µ

Minitab®  – Procedure

  1. Select Stat >> Basic Statistics >> 1 Sample t ...
  2. If it is not already done so, use the pull-down options to select, 'Samples in columns'.
  3. Select the variable you want to analyze by clicking or by highlighting and clicking once on 'Select', so it appears in the box labeled 'Samples in columns'.
  4. In the box labeled 'Test mean', type the assumed value of the mean under the null hypothesis.
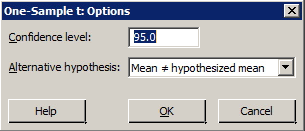
  5. Select Options ... (Ignore the box labeled 'Confidence level'.) For the box labeled 'Alternative', use the pull-down options to select the direction of the alternative hypothesis (less than, not equal, greater than).
  6. Select OK.
  7. Select OK. The output will appear in the session window.

Example

The US National Research Council currently recommends that females between the ages of 11 and 50 intake 15 milligrams of iron daily. The iron intakes of a random sample of 25 such American females are found in the dataset irondef.txt. Is there evidence that the population of American females is, on average, getting less than the recommended 15 mg of iron? That is, should we reject the null hypothesis H0: μ = 15 against the alternative HA: μ < 15?  Using Minitab, determine a 95% confidence interval for μ, the mean iron intake of all women in the population.

Minitab Dialog Boxes

minitab one sample t for the mean dialog box

minitab dialong box for one sample 1 options

Sample Minitab Output

One-Sample T: iron

Test of \(\mu=15 \text { vs }<15\)

Variable N Mean StDev SE Mean 95% Upper Bound T P
iron 25 14.300 2.367 0.473 15.110 -1.48 0.076

Video Review

Randomly Sample Data with Replacement from Columns

Randomly Sample Data with Replacement from Columns

Minitab®  – Procedure

Random sampling from a data set allows one to analyze a subset of the data rather than the entire data set. When you randomly sample "with replacement," you allow the same data point to be selected more than once. Sampling as such helps to ensure that the selected data points are independent.

  1. Select Calc >> Random data >> Sample from columns...
  2. In the box labeled "From columns:", specify the number of data points you want to sample.
  3. In the larger box under the "Sample ... rows from columns" label, specify from which (two) columns you want to sample.
  4. In the box labeled "Store samples in...", specify two unused columns to store your selected data points.
  5. Select (put a checkmark in) the box labeled "Sample with replacement."
  6. Select OK. The randomly sampled data points will appear in the worksheet.

Example

Sports Illustrated published results of a study designed to determine how well professional golfers putt. The data set puttgolf.txt contains data on the lengths of putts and the percentage of successful putts made by professional golfers during 15 tournaments. Only putts that were 2 to 20 feet from the hole are included in the data set.

Randomly sample 5 golfers (with replacement) from the data set.

Minitab Sample from Columns Dialog Box

minitab sample from columns dialog box

Sample Random Selection of 5 Data Points

data points in worksheet

Video Review

Split the Worksheet Based on the Value of a Variable

Split the Worksheet Based on the Value of a Variable

Minitab®  – Procedure

  1. Select Data >> Split Worksheet...
  2. In the box labeled By variables, specify the variable based on which you want the worksheet to be split.
  3. Select OK. The new worksheets, based on the original worksheet, will appear.

Example

A laboratory tested the relationship between operating cost per mile (y = cost) and cruising speed (x = speed) for two different makes (0, 1) of truck tires. The resulting data are stored in tiretesting.txt (Neter, Kutner, et al, 1996, p. 493). Split the worksheet into two worksheets based on the value of the variable make.

Minitab Dialog Box

minitab split worksheet dialog box

Resulting Sample Minitab Output

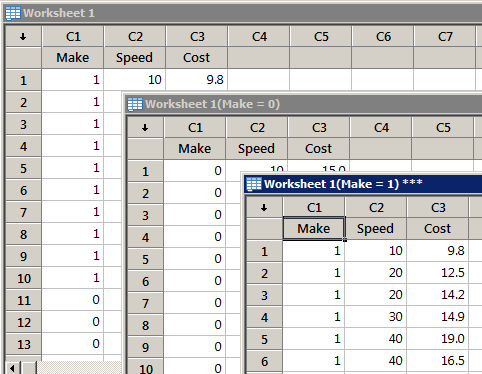
minitab worksheets for each truck make

Worksheet is split into two worksheets; one for each make of truck.

Video Review

Store Residuals, Leverages, and Influence Measures

Store Residuals, Leverages, and Influence Measures

Minitab®  – Procedure

  1. Select Stat >> Regression >> Regression  >> Fit Regression Model ...
  2. Specify the response and the predictor variable(s).
  3. Select Storage... Under Diagnostic Measures, select the type of residuals (and/or influence measures) that you want to be stored. Select OK.
  4. Select OK. The requested residuals (and/or influence measures) will be stored in your worksheet.

Example

The data set adaptive.txt contains the Gesell adaptive scores and ages (in months) of n = 21 children with cyanotic heart disease. Upon regressing the response y = score on the predictor x = age, store the resulting standardized residuals in the worksheet.

Minitab Dialog Boxes

Minitab regression dialog box

Minitab regression dialog box

Minitab Worksheet with a New Column of Stored Residuals

minitab worksheet

Video Review

Legend
[1]Link
↥Has Tooltip/Popover
 Toggleable Visibility