So far, we considered inference to compare two proportions and inference to compare two means. In this section, we will present how to compare two population variances.
Why would we want to compare two population variances? There are many situations, such as in quality control problems, where you may want to choose the process with smaller variability for a variable of interest.
One of the essential steps of a test to compare two population variances is for checking the equal variances assumption if you want to use the pooled variances. Many people use this test as a guide to see if there are any clear violations, much like using the rule of thumb.
When we introduce inference for two parameters before, we started with the sampling distribution. We will not do this here. The details of this test are left out. We will simply present how to use it.
F-Test to Compare Two Population Variances Section
To compare the variances of two quantitative variables, the hypotheses of interest are:
\(H_0\colon \dfrac{\sigma^2_1}{\sigma^2_2}=1\)
\(H_a\colon \dfrac{\sigma^2_1}{\sigma^2_2}\ne1\)
\(H_a\colon \dfrac{\sigma^2_1}{\sigma^2_2}>1\)
\(H_a\colon \dfrac{\sigma^2_1}{\sigma^2_2}<1\)
The last two alternatives are determined by how you arrange your ratio of the two sample statistics.
We will rely on Minitab to conduct this test for us. Minitab offers three (3) different methods to test equal variances.
- The F-test: This test assumes the two samples come from populations that are normally distributed.
- Bonett's test: this assumes only that the two samples are quantitative.
- Levene's test: similar to Bonett's in that the only assumption is that the data is quantitative. Best to use if one or both samples are heavily skewed, and your two sample sizes are both under 20.
Bonett’s test and Levene’s test are both considered nonparametric tests. In our case, since the tests we will be considering are based on a normal distribution, we are expecting to use the F-test. Again, we will need to confirm this by plotting our sample data (i.e., using a probability plot).
Caution! To use the F-test, the samples must come from a normal distribution. The Central Limit Theorem applies to sample means, not to the data. Therefore, if the sample size is large, it does not mean we can assume the data come from a normal distribution.
Example 7-8: Comparing Packing Time Variances Section
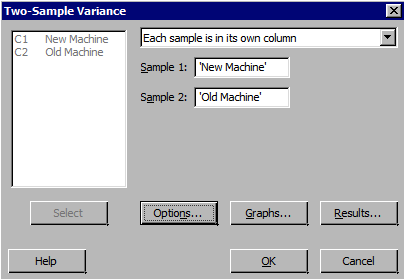
Using the data in the packaging time from our previous discussion on two independent samples, we want to check whether it is reasonable to assume that the two machines have equal population variances.
Recall that the data are given below as (machine.txt):
-
42.1 41.3 42.4 43.2 41.8 41.0 41.8 42.8 42.3 42.7 - \(\bar{x}_1=42.14, \text{s}_1= 0.683\)
-
42.7 43.8 42.5 43.1 44.0 43.6 43.3 43.5 41.7 44.1 - \(\bar{x}_2=43.23, \text{s}_2= 0.750\)
Minitab: F-test to Compare Two Population Variances
In Minitab...
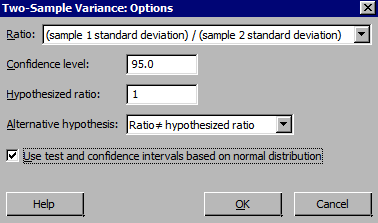
- Choose Stat > Basic Statistics > 2 Variances and complete the dialog boxes.
- In the dialog box, check 'Use test and confidence intervals based on normal distribution' when we are confident the two samples come from a normal distribution.
Notes on using Minitab:
- Minitab will compare the two variances using the popular F-test method.
- If we only have summarized data (e.g. the sample sizes and sample variances or sample standard deviations), then the two variance test in Minitab will only provide an F-test.
- Minitab will use the Bonett and Levene test that are more robust tests when normality is not assumed.
- Minitab calculates the ratio based on Sample 1 divided by Sample 2.
The Minitab Output for the test for equal variances is as follows (a graph is also given in the output that provides confidence intervals and p-value for the test. This is not shown here):
Test and CI for Two Variances: New machine, Old machine
Method
σ1: standard deviation of New machine
σ2: standard deviation of Old machine
Ratio: σ1/σ2
F method was used. This method is accurate for normal data only.
Descriptive Statistics
| Variable | N | StDev | Variance | 95% CI for σ |
|---|---|---|---|---|
| New Machine | 10 | 0.683 | 0.467 | (0.470, 1.248) |
| Old Machine | 10 | 0.750 | 0.562 | (0.516, 1.369) |
Ratio of standard deviations
| Estimated Ratio | 95% CI for Ratio using F |
|---|---|
| 0.911409 | (0454, 1.829) |
Tests
Null hypothesis
Alternative hypothesis
Significance level
H0: σ1/σ2=1
H1: σ1/σ2≠1
α=0.05
| Method | Test Statistic | DF1 | DF2 | P-Value |
|---|---|---|---|---|
| F | 0.83 | 9 | 9 | 0.787 |
How do we interpret the Minitab output?
Note that \(S_{new}=0.683\) and \(s_{old}=0.750\) The test statistic \(F\) is computed as...
\(F=\dfrac{s^2_{new}}{s^2_{old}}=0.83\)
The p-value provided is that for the alternative selected i.e. two-sided. If the alternative were one sided, for example if our alternative in the above example was "ratio less than 1", then the p-value would be half the reported p-value for the two-sided test, or 0.393.
Minitab provided the results only from the F-test since we checked the box to assume normal distribution. Regardless, the hypotheses would be the same for any of the test options and the decision method is the same: if the p-value is less than alpha, we reject the null and conclude the two population variances are not equal. Otherwise, if the p-value is large (i.e. greater than alpha) then we fail to reject the null and can assume the two population variances are equal.
In this example, the p-value for the F-test is very large (larger than 0.1). Therefore, we fail to reject the null hypothesis and conclude that there is not enough evidence to conclude the variances are different.
Note! Remember, if there is doubt about normality, the better choice is to NOT use the F-test. You need to check whether the normal assumption holds before you can use the F-test since the F-test is very sensitive to departure from the normal assumption.
