A common application of the run test is a test for randomness of observations. Because an interest in randomness of observations is quite often seen in a quality-control setting, that's the application that will be the focus of our attention. For example, suppose a quality control supervisor at a paint manufacturing company suspects that the weights of paint cans on the production line are not varying in a random way, as she would expect. Instead, she suspects that the weights are either trending upward or are varying in a cyclic fashion. Every ten minutes, she randomly samples a paint can from the production line, and determines the weights of the randomly selected can.
Let's let \(x_1, x_2, \dots , x_N\) denote the observed weights, where the subscripts designate the order in which the outcomes were obtained. (Note that the textbook uses the letter k here to denote the number of observations in the sample, an unfortunate choice, I think, because we've already taken k to mean something else in this lesson. At any rate, just to be different, and hopefully clearer, I'll use a capital letter N to denote the total number of observations in the sample.) For the sake of concreteness, let's suppose that N is even. If we calculate the median m of the observed weights, then by definition, the median divides the observed sample in half. That is, half of the weights will be less than the median, and half of the weights will be greater than the median. Now, suppose we replace each observation by L if it falls below the median, and by U if it falls above the median.
-
If we observe something like this:
U U U U L U L L L L
then the production process is showing a trend. In this case, we would not observe as many runs r as we would expect if the process were truly random. In this case, we would reject the null hypothesis of randomness, in favor of the alternative hypothesis of a trend effect, if \(r ≤ c\).
-
If we instead observed something like this:
U L U L U L U L U L
then the production process is showing some kind of cyclic event. In this case, we would observe more runs r than we would expect if the process were truly random. In this case, we would reject the null hypothesis of randomness, in favor of the alternative hypothesis of a cyclic effect, if \(r ≥ c\).
-
If we aren't sure in which way a process would deviate from randomness, then we should allow for the possibility of either a trend effect or a cyclic effect. In this case, we should reject the null hypothesis of randomness, in favor of the alternative hypothesis of either a trend effect or a cyclic effect, if \(r ≤ c\) or \(r ≥ c\).
Let's try this idea out on an example!
Example 21-4 Section

A quality control chart has been maintained for the weights of paint cans taken from a conveyor belt at a fixed point in a production line. Sixteen (16) weights obtained today, in order of time, are as follows:
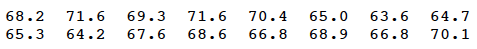
Use the run test, at approximately a 0.01 level, to determine whether the weights of the paint cans on the conveyor belt deviate from randomness.
Answer
With just a bit of ordering work (or using Minitab or some other statistical software), we can readily determine that the median weight of the sampled paint cans is 67.9. Labeling each observed weight with either a U if the observed weight is greater than the median (67.9), or an L if the observed weight is less than the median (67.9), we get:

Counting, we see that we observe 7 runs. Because there is no specific direction given in the possible deviation from randomness, we should test for both trend and cyclic effects. That is, we should reject the null hypothesis if we have either too few or too many runs. That is, our rejection region should be of the form:
\({r : r ≤ c \text{ or } r ≥ c}\)
Because we have a sample size of N = 16, we'll use the p.m.f. of R with \(n_1 = 8\) and \(n_2 = 8\). Now, using the formulas with k = 1 and k = 8, we get:
\[P(R=2)=\dfrac{2\binom{7}{0}\binom{7}{0}}{\binom{16}{8}}=\dfrac{2\binom{7}{7}\binom{7}{7}}{\binom{16}{8}} =P(R=16)=\dfrac{2}{12,870} \]
Using the formulas with k = 1 and k = 7, we get:
\[P(R=3)=\dfrac{\binom{7}{1}\binom{7}{0}+\binom{7}{1}\binom{7}{0}}{\binom{16}{8}}=\dfrac{\binom{7}{7}\binom{7}{6}+\binom{7}{7}\binom{7}{6}}{\binom{16}{8}}=P(R=15)=\dfrac{14}{12,870} \]
And, using the formulas with k = 2 and k = 7, we get:
\[P(R=4)=\dfrac{2\binom{7}{1}\binom{7}{1}}{\binom{16}{8}}=\dfrac{2\binom{7}{6}\binom{7}{6}}{\binom{16}{8}} =P(R=14)=\dfrac{98}{12,870} \]
Therefore, the critical region \({r : r ≤ 4 \text{ or } r ≥ 14}\) would yield a test at a significance level of:
\[\alpha = P(R \le 4)+P(R \ge 14)=\dfrac{2+14+98}{12,870}+\dfrac{2+14+98}{12,870}=\dfrac{228}{12,870}=0.018\]
The 7 runs we observed does not fall in our proposed rejection region. Therefore, we fail to reject at the 0.018 significance level. There is insufficient evidence at the 0.018 level to conclude that the process has deviated from randomness.
Notes Section
- In both the discussion and the example above, the sample size N was even. What happens if the sample size N is odd? Well, in that case, when we divide the sample up into those below (L) and those above (U) the median, the number of observations in the "upper half" and the "lower half" will differ by one. If that's the case, the standard protocol is to put the extra observation in the "upper half." In that case, \(n_2 = n_1 + 1\).
- If the median is equal to a value that is tied with other values, standard protocol again puts the tied values in the "upper half," and the test is performed with \(n_1\) and \(n_2\) being unequal.