In each of the examples we considered so far in this lesson, there is one and only one parameter. What happens if a probability distribution has two parameters, \(\theta_1\) and \(\theta_2\), say, for which we want to find sufficient statistics, \(Y_1\) and \(Y_2\)? Fortunately, the definitions of sufficiency can easily be extended to accommodate two (or more) parameters. Let's start by extending the Factorization Theorem.
- Definition (Factorization Theorem)
-
Let \(X_1, X_2, \ldots, X_n\) denote random variables with a joint p.d.f. (or joint p.m.f.):
\( f(x_1,x_2, ... ,x_n; \theta_1, \theta_2) \)
which depends on the parameters \(\theta_1\) and \(\theta_2\). Then, the statistics \(Y_1=u_1(X_1, X_2, ... , X_n)\) and \(Y_2=u_2(X_1, X_2, ... , X_n)\) are joint sufficient statistics for \(\theta_1\) and \(\theta_2\) if and only if:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) =\phi\left[u_1(x_1, ... , x_n), u_2(x_1, ... , x_n);\theta_1, \theta_2 \right] h(x_1, ... , x_n)\)
where:
- \(\phi\) is a function that depends on the data \((x_1, x_2, ... , x_n)\) only through the functions \(u_1(x_1, x_2, ... , x_n)\) and \(u_2(x_1, x_2, ... , x_n)\), and
- the function \(h(x_1, ... , x_n)\) does not depend on either of the parameters \(\theta_1\) or \(\theta_2\).
Let's try the extended theorem out for size on an example.
Example 24-6 Section

Let \(X_1, X_2, \ldots, X_n\) denote a random sample from a normal distribution \(N(\theta_1, \theta_2\). That is, \(\theta_1\) denotes the mean \(\mu\) and \(\theta_2\) denotes the variance \(\sigma^2\). Use the Factorization Theorem to find joint sufficient statistics for \(\theta_1\) and \(\theta_2\).
Answer
Because \(X_1, X_2, \ldots, X_n\) is a random sample, the joint probability density function of \(X_1, X_2, \ldots, X_n\) is, by independence:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) = f(x_1;\theta_1, \theta_2) \times f(x_2;\theta_1, \theta_2) \times ... \times f(x_n;\theta_1, \theta_2) \times \)
Inserting what we know to be the probability density function of a normal random variable with mean \(\theta_1\) and variance \(\theta_2\), the joint p.d.f. is:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) = \dfrac{1}{\sqrt{2\pi\theta_2}} \text{exp} \left[-\dfrac{1}{2}\dfrac{(x_1-\theta_1)^2}{\theta_2} \right] \times ... \times = \dfrac{1}{\sqrt{2\pi\theta_2}} \text{exp} \left[-\dfrac{1}{2}\dfrac{(x_n-\theta_1)^2}{\theta_2} \right] \)
Simplifying by collecting like terms, we get:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) = \left(\dfrac{1}{\sqrt{2\pi\theta_2}}\right)^n \text{exp} \left[-\dfrac{1}{2}\dfrac{\sum_{i=1}^{n}(x_i-\theta_1)^2}{\theta_2} \right] \)
Rewriting the first factor, and squaring the quantity in parentheses, and distributing the summation, in the second factor, we get:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) = \text{exp} \left[\text{log}\left(\dfrac{1}{\sqrt{2\pi\theta_2}}\right)^n\right] \text{exp} \left[-\dfrac{1}{2\theta_2}\left\{ \sum_{i=1}^{n}x_{i}^{2} -2\theta_1\sum_{i=1}^{n}x_{i} +\sum_{i=1}^{n}\theta_{1}^{2} \right\}\right] \)
Simplifying yet more, we get:
\(f(x_1, x_2, ... , x_n;\theta_1, \theta_2) = \text{exp} \left[ -\dfrac{1}{2\theta_2}\sum_{i=1}^{n}x_{i}^{2}+\dfrac{\theta_1}{\theta_2}\sum_{i=1}^{n}x_{i} -\dfrac{n\theta_{1}^{2}}{2\theta_2}-n\text{log}\sqrt{2\pi\theta_2} \right]\)
Look at that! We have factored the joint p.d.f. into two functions, one (\(\phi\)) being only a function of the statistics \(Y_1=\sum_{i=1}^{n}X^{2}_{i}\) and \(Y_2=\sum_{i=1}^{n}X_i\), and the other (h) not depending on the parameters \(\theta_1\) and \(\theta_2\):
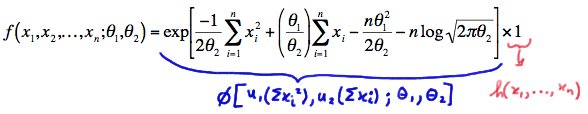
Therefore, the Factorization Theorem tells us that \(Y_1=\sum_{i=1}^{n}X^{2}_{i}\) and \(Y_2=\sum_{i=1}^{n}X_i\) are joint sufficient statistics for \(\theta_1\) and \(\theta_2\). And, the one-to-one functions of \(Y_1\) and \(Y_2\), namely:
\( \bar{X} =\dfrac{Y_2}{n}=\dfrac{1}{n}\sum_{i=1}^{n}X_i \)
and
\( S_2=\dfrac{Y_1-(Y_{2}^{2}/n)}{n-1}=\dfrac{1}{n-1} \left[\sum_{i=1}^{n}X_{i}^{2}-n\bar{X}^2 \right] \)
are also joint sufficient statistics for \(\theta_1\) and \(\theta_2\). Aha! We have just shown that the intuitive estimators of \(\mu\) and \(\sigma^2\) are also sufficient estimators. That is, the data contain no more information than the estimators \(\bar{X}\) and \(S^2\) do about the parameters \(\mu\) and \(\sigma^2\)! That seems like a good thing!
We have just extended the Factorization Theorem. Now, the Exponential Criterion can also be extended to accommodate two (or more) parameters. It is stated here without proof.
Exponential Criterion Section
Let \(X_1, X_2, \ldots, X_n\) be a random sample from a distribution with a p.d.f. or p.m.f. of the exponential form:
\( f(x;\theta_1,\theta_2)=\text{exp}\left[K_1(x)p_1(\theta_1,\theta_2)+K_2(x)p_2(\theta_1,\theta_2)+S(x) +q(\theta_1,\theta_2) \right] \)
with a support that does not depend on the parameters \(\theta_1\) and \(\theta_2\). Then, the statistics \(Y_1=\sum_{i=1}^{n}K_1(X_i)\) and \(Y_2=\sum_{i=1}^{n}K_2(X_i)\) are jointly sufficient for \(\theta_1\) and \(\theta_2\).
Let's try applying the extended exponential criterion to our previous example.
Example 24-6 continuted Section

Let \(X_1, X_2, \ldots, X_n\) denote a random sample from a normal distribution \(N(\theta_1, \theta_2)\). That is, \(\theta_1\) denotes the mean \(\mu\) and \(\theta_2\) denotes the variance \(\sigma^2\). Use the Exponential Criterion to find joint sufficient statistics for \(\theta_1\) and \(\theta_2\).
Answer
The probability density function of a normal random variable with mean \(\theta_1\) and variance \(\theta_2\) can be written in exponential form as:
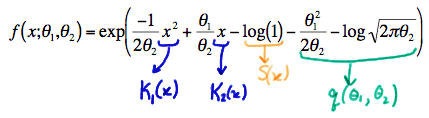
Therefore, the statistics \(Y_1=\sum_{i=1}^{n}X^{2}_{i}\) and \(Y_2=\sum_{i=1}^{n}X_i\) are joint sufficient statistics for \(\theta_1\) and \(\theta_2\).