Example 23-1 Section
Here's an example that illustrates how a Bayesian might use available data to assign probabilities to particular events.
The following amounts, in dollars, are bet on horses A, B, C, and D to win a local race:
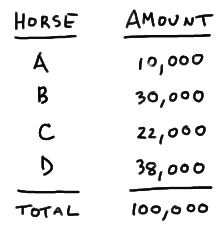
Determine the payout for winning with a \$2 bet on each of the four horses, if the track wants to take 17%, or \$17,000, from the amount collected.
Answer
The first thing we need to do is to determine the likelihood, that is, probability, that each of the horses wins. We could assign the probabilities based on our own "gut feeling." Geez.... I think horse A is gonna win today. In general, that's probably not a good idea. We'd probably be much better served if we used the information we have available, namely the "gut feeling" of all of the bettors! That is, if \$38,000 worth of bets came in for Horse D and only \$10,000 came in for Horse A, that tells us that more people think that Horse D is going to win than Horse A. It would behoove us, therefore, to use the amounts bet to assign the probabilities. That said, the probability that Horse A will win is then:
\(P(A) = \dfrac{10,000}{100,000}=0.10\)
And, the probability that Horse B will win is:
\(P(B) = \dfrac{30,000}{100,000}=0.30\)
And, the probability that Horse C will win is:
\(P(C) = \dfrac{22,000}{100,000}=0.22\)
And, the probability that Horse D will win is:
\(P(D) = \dfrac{38,000}{100,000}=0.38\)
Now having assigned a probability to the event that Horse A wins, we can determine the odds against horse A winning. It is:
\(\text{Odds against } A = \dfrac{1-0.10}{0.10}= 9 \text{ to } 1 \)
The odds against A tells us that the track will payout \$9 on a \$1 bet. Now, the odds against Horse B winning is:
\(\text{Odds against } B = \dfrac{1-0.30}{0.30}= \dfrac{7}{3} \text{ to } 1 \)
The odds against B tells us that the track will payout \(\frac{\$7}{3}=\$2.33\) on a \$1 bet. Now, the odds against Horse C winning is:
\(\text{Odds against } C = \dfrac{1-0.22}{0.22}= \dfrac{39}{11} \text{ to } 1 \)
The odds against C tells us that the track will payout \(\dfrac{\$39}{11}=\$3.55\) on a \$1 bet. Finally, the odds against Horse D winning is:
\(\text{Odds against } D = \dfrac{1-0.38}{0.38}= \dfrac{31}{19} \text{ to } 1 \)
The odds against D tells us that the track will payout \(\dfrac{\$31}{19}=\$1.63\) on a \$1 bet. Now, using the odds against Horse A winning, we can determine that the amount the track pays out on a \$2 bet on Horse A is:
\(\text{Payout for } A = $2 + 9($2) = $20 \)
That is, the bettor gets \$9 for each \$1 bet, that is, \$18, plus the \$2 he or she originally bet. Now, using the odds against Horse B winning, we can determine that the amount the track pays out on a \$2 bet on Horse B is:
\(\text{Payout for } B = $2 + \dfrac{7}{3}($2) = $6.67 \)
And, using the odds against Horse C winning, we can determine that the amount the track pays out on a \$2 bet on Horse C is:
\(\text{Payout for } C = $2 + \dfrac{39}{11}($2) = $9.09 \)
And, using the odds against Horse D winning, we can determine that the amount the track pays out on a \$2 bet on Horse D is:
\(\text{Payout for } D = $2 + \dfrac{31}{19}($2) = $5.26 \)
We're almost there. We just need to skim the 17% off for the race track to make sure that it makes some money off of the bettors. Multiplying each of the calculated payouts by 0.83, we get:
\(\text{Absolute payout for } A = $20.00(0.83) = $16.60 \)
\(\text{Absolute payout for } B = $6.67(0.83) = $5.54 \)
\(\text{Absolute payout for } C = $9.09(0.83) = $7.54 \)
\(\text{Absolute payout for } D = $5.26(0.83) = $4.37 \)
We can always check our work, too. Suppose, for example, that Horse A wins. Then the track would payout \$16.60 to the 5000 bettors who bet \$2 on Horse A, costing the track \$16.60(5000) = \$83,000. Given that that track brought in \$100,000 in bets, the track would indeed make its desired \$17,000. A similar check of our work can be made for Horses B, C, and D, although there may be some round-off errors because we did do some rounding in our payout calculations. Should still be very close to \$83,000 in each case though!