As we'll soon see, the confidence interval for the ratio of two variances requires the use of the probability distribution known as the F-distribution. So, let's spend a few minutes learning the definition and characteristics of the F-distribution.
- F-distribution
-
If U and V are independent chi-square random variables with \(r_1\) and \(r_2\) degrees of freedom, respectively, then:
\(F=\dfrac{U/r_1}{V/r_2}\)
follows an F-distribution with \(r_1\) numerator degrees of freedom and \(r_2\) denominator degrees of freedom. We write F ~ F(\(r_1\), \(r_2\)).
Characteristics of the F-Distribution Section
-
F-distributions are generally skewed. The shape of an F-distribution depends on the values of \(r_1\) and \(r_2\), the numerator and denominator degrees of freedom, respectively, as this picture pirated from your textbook illustrates:
-
The probability density function of an F random variable with \(r_1\) numerator degrees of freedom and \(r_2\) denominator degrees of freedom is:
\(f(w)=\dfrac{(r_1/r_2)^{r_1/2}\Gamma[(r_1+r_2)/2]w^{(r_1/2)-1}}{\Gamma[r_1/2]\Gamma[r_2/2][1+(r_1w/r_2)]^{(r_1+r_2)/2}}\)
over the support \(w ≥ 0\).
-
The definition of an F-random variable:
\(F=\dfrac{U/r_1}{V/r_2}\)
implies that if the distribution of W is F(\(r_1\), \(r_2\)), then the distribution of 1/W is F(\(r_2\), \(r_1\)).
The F-Table Section
One of the primary ways that we will need to interact with an F-distribution is by needing to know either:
- An F-value, or
- The probabilities associated with an F-random variable, in order to complete a statistical analysis.
We could go ahead and try to work with the above probability density function to find the necessary values, but I think you'll agree before long that we should just turn to an F-table, and let it do the dirty work for us. For that reason, we'll now explore how to use a typical F-table to look up F-values and/or F-probabilities. Let's start with two definitions.
- \(100 \alpha^{th}\) percentile
-
Let \(\alpha\) be some probability between 0 and 1 (most often, a small probability less than 0.10). The upper \(100 \alpha^{th}\) percentile of an F-distribution with \(r_1\) and \(r_2\) degrees of freedom is the value \(F_\alpha(r_1,r_2)\) such that the area under the curve and to the right of \(F_\alpha(r_1,r_2)\) is \(\alpha\):
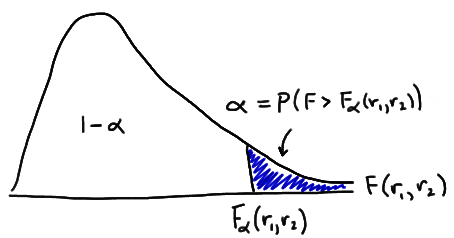
The above definition is used in Table VII, the F-distribution table in the back of your textbook. While the next definition is not used directly in Table VII, you'll still find it necessary when looking for F-values (or F-probabilities) in the left tail of an F-distribution.
- \(100 \alpha^{th}\) percentile
-
Let \(\alpha\) be some probability between 0 and 1 (most often, a small probability less than 0.10). The \(100 \alpha^{th}\) percentile of an F-distribution with \(r_1\) and \(r_2\) degrees of freedom is the value \(F_{1-\alpha}(r_1,r_2)\) such that the area under the curve and to the right of \(F_{1-\alpha}(r_1,r_2)\) is 1−\(\alpha\):
With the two definitions behind us, let's now take a look at the F-table in the back of your textbook.
In summary, here are the steps you should take in using the F>-table to find an F-value:
- Find the column that corresponds to the relevant numerator degrees of freedom, \(r_1\).
- Find the three rows that correspond to the relevant denominator degrees of freedom, \(r_2\).
- Find the one row, from the group of three rows identified in the second step, that is headed by the probability of interest... whether it's 0.01, 0.025, 0.05.
- Determine the F-value where the \(r_1\) column and the probability row identified in step 3 intersect.
Now, at least theoretically, you could also use the F-table to find the probability associated with a particular F-value. But, as you can see, the table is pretty (very!) limited in that direction. For example, if you have an F random variable with 6 numerator degrees of freedom and 2 denominator degrees of freedom, you could only find the probabilities associated with the F values of 19.33, 39.33, and 99.33:
| \(P(F ≤ f)\) = \(\displaystyle \int^f_0\dfrac{\Gamma[(r_1+r_2)/2](r_1/r_2)^{r_1/2}w^{(r_1/2)-1}}{\Gamma[r_1/2]\Gamma[r_2/2][1+(r_1w/r_2)]^{(r_1+r_2)/2}}dw\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(\alpha\) | \(P(F ≤ f)\) | Den. d.f. \(r_2\) |
Numerator Degrees of Freedom, \(r_1\) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
1 | 161.40 647.74 4052.00 |
199.50 799.50 4999.50 |
215.70 864.16 5403.00 |
224.60 899.58 5625.00 |
230.20 921.85 5764.00 |
234.00 937.11 5859.00 |
236.80 948.22 5928.00 |
238.90 956.66 5981.00 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
2 | 18.51 38.51 98.50 |
19.00 39.00 99.00 |
19.16 39.17 99.17 |
19.25 39.25 99.25 |
19.30 39.30 99.30 |
19.33 39.33 99.33 |
19.35 39.36 99.36 |
19.37 39.37 99.37 |
What would you do if you wanted to find the probability that an F random variable with 6 numerator degrees of freedom and 2 denominator degrees of freedom was less than 6.2, say? Well, the answer is, of course... statistical software, such as SAS or Minitab! For what we'll be doing, the F table will (mostly) serve our purpose. When it doesn't, we'll use Minitab. At any rate, let's get a bit more practice now using the F table.
Example 4-2 Section
Let X be an F random variable with 4 numerator degrees of freedom and 5 denominator degrees of freedom. What is the upper fifth percentile?
Answer
The upper fifth percentile is the F-value x such that the probability to the right of x is 0.05, and therefore the probability to the left of x is 0.95. To find x using the F-table, we:
- Find the column headed by \(r_1 = 4\).
- Find the three rows that correspond to \(r_2 = 5\).
- Find the one row, from the group of three rows identified in the above step, that is headed by \(\alpha = 0.05\) (and \(P(X ≤ x) = 0.95\).
Now, all we need to do is read the F-value where the \(r_1 = 4\) column and the identified \(\alpha = 0.05\) row intersect. What do you get?
| \(P(F ≤ f)\) = \(\displaystyle \int^f_0\dfrac{\Gamma[(r_1+r_2)/2](r_1/r_2)^{r_1/2}w^{(r_1/2)-1}}{\Gamma[r_1/2]\Gamma[r_2/2][1+(r_1w/r_2)]^{(r_1+r_2)/2}}dw\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(\alpha\) | \(P(F ≤ f)\) | Den. d.f. \(r_2\) |
Numerator Degrees of Freedom, \(r_1\) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
1 | 161.40 647.74 4052.00 |
199.50 799.50 4999.50 |
215.70 864.16 5403.00 |
224.60 899.58 5625.00 |
230.20 921.85 5764.00 |
234.00 937.11 5859.00 |
236.80 948.22 5928.00 |
238.90 956.66 5981.00 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
2 | 18.51 38.51 98.50 |
19.00 39.00 99.00 |
19.16 39.17 99.17 |
19.25 39.25 99.25 |
19.30 39.30 99.30 |
19.33 39.33 99.33 |
19.35 39.36 99.36 |
19.37 39.37 99.37 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
3 | 10.13 17.44 34.12 |
9.55 16.04 30.82 |
9.28 15.44 29.46 |
9.12 15.10 28.71 |
9.01 14.88 28.24 |
8.94 14.73 27.91 |
8.89 14.62 27.67 |
8.85 14.54 27.49 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
4 | 7.71 12.22 21.20 |
6.94 10.65 18.00 |
6.59 9.98 16.69 |
6.39 9.60 15.98 |
6.26 9.36 15.52 |
6.16 9.20 15.21 |
6.09 9.07 14.98 |
6.04 8.98 14.80 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
5 | 6.61 10.01 16.26 |
5.79 8.43 13.27 |
5.41 7.76 12.06 |
5.19 7.39 11.39 |
5.05 7.15 10.97 |
4.95 6.98 10.67 |
4.88 6.85 10.46 |
4.82 6.76 10.29 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
6 |
5.99 |
5.14 7.26 10.92 |
4.76 6.60 9.78 |
4.53 6.23 9.15 |
4.39 5.99 8.75 |
4.28 5.82 8.47 |
4.21 5.70 8.26 |
4.15 5.60 8.10 |
| \(P(F ≤ f)\) = \(\displaystyle \int^f_0\dfrac{\Gamma[(r_1+r_2)/2](r_1/r_2)^{r_1/2}w^{(r_1/2)-1}}{\Gamma[r_1/2]\Gamma[r_2/2][1+(r_1w/r_2)]^{(r_1+r_2)/2}}dw\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(\alpha\) | \(P(F ≤ f)\) | Den. d.f. \(r_2\) |
Numerator Degrees of Freedom, \(r_1\) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
1 | 161.40 647.74 4052.00 |
199.50 799.50 4999.50 |
215.70 864.16 5403.00 |
224.60 899.58 5625.00 |
230.20 921.85 5764.00 |
234.00 937.11 5859.00 |
236.80 948.22 5928.00 |
238.90 956.66 5981.00 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
2 | 18.51 38.51 98.50 |
19.00 39.00 99.00 |
19.16 39.17 99.17 |
19.25 39.25 99.25 |
19.30 39.30 99.30 |
19.33 39.33 99.33 |
19.35 39.36 99.36 |
19.37 39.37 99.37 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
3 | 10.13 17.44 34.12 |
9.55 16.04 30.82 |
9.28 15.44 29.46 |
9.12 15.10 28.71 |
9.01 14.88 28.24 |
8.94 14.73 27.91 |
8.89 14.62 27.67 |
8.85 14.54 27.49 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
4 | 7.71 12.22 21.20 |
6.94 10.65 18.00 |
6.59 9.98 16.69 |
6.39 9.60 15.98 |
6.26 9.36 15.52 |
6.16 9.20 15.21 |
6.09 9.07 14.98 |
6.04 8.98 14.80 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
5 | 6.61 10.01 16.26 |
5.79 8.43 13.27 |
5.41 7.76 12.06 |
5.19 7.39 11.39 |
5.05 7.15 10.97 |
4.95 6.98 10.67 |
4.88 6.85 10.46 |
4.82 6.76 10.29 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
6 |
5.99 |
5.14 7.26 10.92 |
4.76 6.60 9.78 |
4.53 6.23 9.15 |
4.39 5.99 8.75 |
4.28 5.82 8.47 |
4.21 5.70 8.26 |
4.15 5.60 8.10 |
The table tells us that the upper fifth percentile of an F random variable with 4 numerator degrees of freedom and 5 denominator degrees of freedom is 5.19.
Let X be an F random variable with 4 numerator degrees of freedom and 5 denominator degrees of freedom. What is the first percentile?
Answer
The first percentile is the F-value x such that the probability to the left of x is 0.01 (and hence the probability to the right of x is 0.99). Since such an F-value isn't directly readable from the F-table, we need to do a little finagling to find x using the F-table. That is, we need to recognize that the F-value we are looking for, namely \(F_{0.99}(4,5)\), is related to \(F_{0.01}(5,4)\), a value we can read off of the table by way of this relationship:
\(F_{0.99}(4,5)=\dfrac{1}{F_{0.01}(5,4)}\)
That said, to find x using the F-table, we:
- Find the column headed by \(r_1 = 5\).
- Find the three rows that correspond to \(r_2 = 4\).
- Find the one row, from the group of three rows identified in (2), that is headed by \(\alpha = 0.01\) (and \(P(X ≤ x) = 0.99\).
Now, all we need to do is read the F-value where the \(r_1 = 5\) column and the identified \(\alpha = 0.01\) row intersect, and take the inverse. What do you get?
| \(P(F ≤ f)\) = \(\displaystyle \int^f_0\dfrac{\Gamma[(r_1+r_2)/2](r_1/r_2)^{r_1/2}w^{(r_1/2)-1}}{\Gamma[r_1/2]\Gamma[r_2/2][1+(r_1w/r_2)]^{(r_1+r_2)/2}}dw\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(\alpha\) | \(P(F ≤ f)\) | Den. d.f. \(r_2\) |
Numerator Degrees of Freedom, \(r_1\) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
1 | 161.40 647.74 4052.00 |
199.50 799.50 4999.50 |
215.70 864.16 5403.00 |
224.60 899.58 5625.00 |
230.20 921.85 5764.00 |
234.00 937.11 5859.00 |
236.80 948.22 5928.00 |
238.90 956.66 5981.00 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
2 | 18.51 38.51 98.50 |
19.00 39.00 99.00 |
19.16 39.17 99.17 |
19.25 39.25 99.25 |
19.30 39.30 99.30 |
19.33 39.33 99.33 |
19.35 39.36 99.36 |
19.37 39.37 99.37 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
3 | 10.13 17.44 34.12 |
9.55 16.04 30.82 |
9.28 15.44 29.46 |
9.12 15.10 28.71 |
9.01 14.88 28.24 |
8.94 14.73 27.91 |
8.89 14.62 27.67 |
8.85 14.54 27.49 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
4 | 7.71 12.22 21.20 |
6.94 10.65 18.00 |
6.59 9.98 16.69 |
6.39 9.60 15.98 |
6.26 9.36 15.52 |
6.16 9.20 15.21 |
6.09 9.07 14.98 |
6.04 8.98 14.80 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
5 | 6.61 10.01 16.26 |
5.79 8.43 13.27 |
5.41 7.76 12.06 |
5.19 7.39 11.39 |
5.05 7.15 10.97 |
4.95 6.98 10.67 |
4.88 6.85 10.46 |
4.82 6.76 10.29 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
6 |
5.99 |
5.14 7.26 10.92 |
4.76 6.60 9.78 |
4.53 6.23 9.15 |
4.39 5.99 8.75 |
4.28 5.82 8.47 |
4.21 5.70 8.26 |
4.15 5.60 8.10 |
| \(P(F ≤ f)\) = \(\displaystyle \int^f_0\dfrac{\Gamma[(r_1+r_2)/2](r_1/r_2)^{r_1/2}w^{(r_1/2)-1}}{\Gamma[r_1/2]\Gamma[r_2/2][1+(r_1w/r_2)]^{(r_1+r_2)/2}}dw\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(\alpha\) | \(P(F ≤ f)\) | Den. d.f. \(r_2\) |
Numerator Degrees of Freedom, \(r_1\) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
1 | 161.40 647.74 4052.00 |
199.50 799.50 4999.50 |
215.70 864.16 5403.00 |
224.60 899.58 5625.00 |
230.20 921.85 5764.00 |
234.00 937.11 5859.00 |
236.80 948.22 5928.00 |
238.90 956.66 5981.00 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
2 | 18.51 38.51 98.50 |
19.00 39.00 99.00 |
19.16 39.17 99.17 |
19.25 39.25 99.25 |
19.30 39.30 99.30 |
19.33 39.33 99.33 |
19.35 39.36 99.36 |
19.37 39.37 99.37 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
3 | 10.13 17.44 34.12 |
9.55 16.04 30.82 |
9.28 15.44 29.46 |
9.12 15.10 28.71 |
9.01 14.88 28.24 |
8.94 14.73 27.91 |
8.89 14.62 27.67 |
8.85 14.54 27.49 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
4 | 7.71 12.22 21.20 |
6.94 10.65 18.00 |
6.59 9.98 16.69 |
6.39 9.60 15.98 |
6.26 9.36 15.52 |
6.16 9.20 15.21 |
6.09 9.07 14.98 |
6.04 8.98 14.80 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
5 | 6.61 10.01 16.26 |
5.79 8.43 13.27 |
5.41 7.76 12.06 |
5.19 7.39 11.39 |
5.05 7.15 10.97 |
4.95 6.98 10.67 |
4.88 6.85 10.46 |
4.82 6.76 10.29 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
6 |
5.99 |
5.14 7.26 10.92 |
4.76 6.60 9.78 |
4.53 6.23 9.15 |
4.39 5.99 8.75 |
4.28 5.82 8.47 |
4.21 5.70 8.26 |
4.15 5.60 8.10 |
The table, along with a minor calculation, tells us that the first percentile of an F random variable with 4 numerator degrees of freedom and 5 denominator degrees of freedom is 1/15.52 = 0.064.
What is the probability that an F random variable with 4 numerator degrees of freedom and 5 denominator degrees of freedom is greater than 7.39?
Answer
There I go... just a minute ago, I said that the F-table isn't very helpful in finding probabilities, then I turn around and ask you to use the table to find a probability! Doing it at least once helps us make sure that we fully understand the table. In this case, we are going to need to read the table "backwards." To find the probability, we:
- Find the column headed by \(r_1 = 4\).
- Find the three rows that correspond to \(r_2 = 5\).
- Find the one row, from the group of three rows identified in the second point above, that contains the value 7.39 in the \(r_1 = 4\) column.
- Read the value of \(\alpha\) that heads the row in which the 7.39 falls.
What do you get?
| \(P(F ≤ f)\) = \(\displaystyle \int^f_0\dfrac{\Gamma[(r_1+r_2)/2](r_1/r_2)^{r_1/2}w^{(r_1/2)-1}}{\Gamma[r_1/2]\Gamma[r_2/2][1+(r_1w/r_2)]^{(r_1+r_2)/2}}dw\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(\alpha\) | \(P(F ≤ f)\) | Den. d.f. \(r_2\) |
Numerator Degrees of Freedom, \(r_1\) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
1 | 161.40 647.74 4052.00 |
199.50 799.50 4999.50 |
215.70 864.16 5403.00 |
224.60 899.58 5625.00 |
230.20 921.85 5764.00 |
234.00 937.11 5859.00 |
236.80 948.22 5928.00 |
238.90 956.66 5981.00 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
2 | 18.51 38.51 98.50 |
19.00 39.00 99.00 |
19.16 39.17 99.17 |
19.25 39.25 99.25 |
19.30 39.30 99.30 |
19.33 39.33 99.33 |
19.35 39.36 99.36 |
19.37 39.37 99.37 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
3 | 10.13 17.44 34.12 |
9.55 16.04 30.82 |
9.28 15.44 29.46 |
9.12 15.10 28.71 |
9.01 14.88 28.24 |
8.94 14.73 27.91 |
8.89 14.62 27.67 |
8.85 14.54 27.49 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
4 | 7.71 12.22 21.20 |
6.94 10.65 18.00 |
6.59 9.98 16.69 |
6.39 9.60 15.98 |
6.26 9.36 15.52 |
6.16 9.20 15.21 |
6.09 9.07 14.98 |
6.04 8.98 14.80 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
5 | 6.61 10.01 16.26 |
5.79 8.43 13.27 |
5.41 7.76 12.06 |
5.19 7.39 11.39 |
5.05 7.15 10.97 |
4.95 6.98 10.67 |
4.88 6.85 10.46 |
4.82 6.76 10.29 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
6 |
5.99 |
5.14 7.26 10.92 |
4.76 6.60 9.78 |
4.53 6.23 9.15 |
4.39 5.99 8.75 |
4.28 5.82 8.47 |
4.21 5.70 8.26 |
4.15 5.60 8.10 |
| \(P(F ≤ f)\) = \(\displaystyle \int^f_0\dfrac{\Gamma[(r_1+r_2)/2](r_1/r_2)^{r_1/2}w^{(r_1/2)-1}}{\Gamma[r_1/2]\Gamma[r_2/2][1+(r_1w/r_2)]^{(r_1+r_2)/2}}dw\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(\alpha\) | \(P(F ≤ f)\) | Den. d.f. \(r_2\) |
Numerator Degrees of Freedom, \(r_1\) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
1 | 161.40 647.74 4052.00 |
199.50 799.50 4999.50 |
215.70 864.16 5403.00 |
224.60 899.58 5625.00 |
230.20 921.85 5764.00 |
234.00 937.11 5859.00 |
236.80 948.22 5928.00 |
238.90 956.66 5981.00 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
2 | 18.51 38.51 98.50 |
19.00 39.00 99.00 |
19.16 39.17 99.17 |
19.25 39.25 99.25 |
19.30 39.30 99.30 |
19.33 39.33 99.33 |
19.35 39.36 99.36 |
19.37 39.37 99.37 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
3 | 10.13 17.44 34.12 |
9.55 16.04 30.82 |
9.28 15.44 29.46 |
9.12 15.10 28.71 |
9.01 14.88 28.24 |
8.94 14.73 27.91 |
8.89 14.62 27.67 |
8.85 14.54 27.49 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
4 | 7.71 12.22 21.20 |
6.94 10.65 18.00 |
6.59 9.98 16.69 |
6.39 9.60 15.98 |
6.26 9.36 15.52 |
6.16 9.20 15.21 |
6.09 9.07 14.98 |
6.04 8.98 14.80 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
5 | 6.61 10.01 16.26 |
5.79 8.43 13.27 |
5.41 7.76 12.06 |
5.19 7.39 11.39 |
5.05 7.15 10.97 |
4.95 6.98 10.67 |
4.88 6.85 10.46 |
4.82 6.76 10.29 |
| 0.05 0.0025 0.01 |
0.95 0.975 0.99 |
6 |
5.99 |
5.14 7.26 10.92 |
4.76 6.60 9.78 |
4.53 6.23 9.15 |
4.39 5.99 8.75 |
4.28 5.82 8.47 |
4.21 5.70 8.26 |
4.15 5.60 8.10 |
The table tells us that the probability that an F random variable with 4 numerator degrees of freedom and 5 denominator degrees of freedom is greater than 7.39 is 0.025.