Construct a correlation matrix to examine the relationship between how many hours per week students exercise, their heights, their weights, and their resting pulse rates.

This example uses the 'StudentSurvey' dataset from the Lock⁵ textbook. The data was collected from a sample of 362 college students.

  To construct a correlation matrix in Minitab...

1. Open the Minitab file: StudentSurvey.mpx
2. Select Stat > Basic Statistics > Correlation
3. Enter the variables Exercise, Height, Weight and Pulse into the Variables box
4. Select the Graphs... button and select Correlations and p-values from the dropdown
5. Select the Results... button and verify that the Correlation matrix and the Pairwise correlation table boxes are checked
6. Click OK and OK

This should result in the following output:

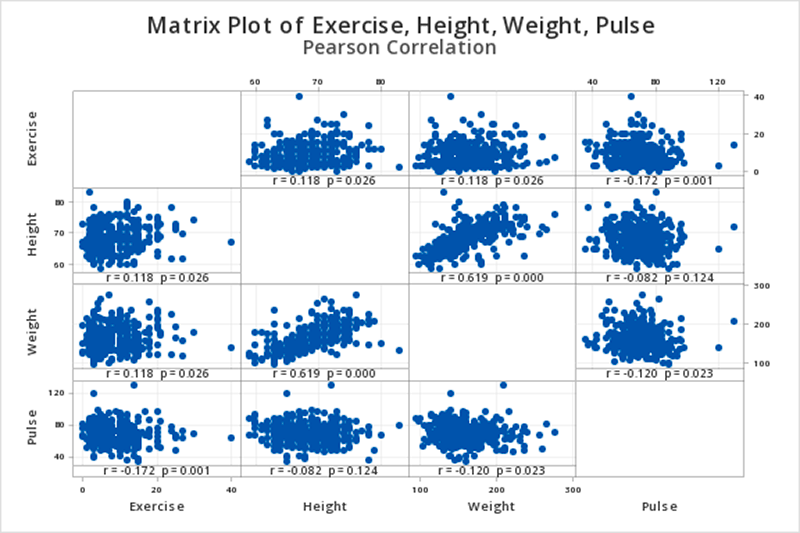
Correlation

	Exercise	Height	Weight
Height	0.118
Weight	0.118	0.619
Pulse	-0.172	-0.082	-0.120

Pairwise Pearson Correlations

Sample 1	Sample 2	N	Correlation	95% CI for ρ	P-Value
Height	Exercise	354	0.118	(0.014, 0.220)	0.026
Weight	Exercise	356	0.118	(0.015, 0.220)	0.026
Pulse	Exercise	361	-0.172	(-0.271, -0.071)	0.001
Weight	Height	352	0.619	(0.551, 0.680)	0.000
Pulse	Height	355	-0.082	(-0.184, 0.023)	0.124
Pulse	Weight	357	-0.120	(-0.221, -0.016)	0.023

Interpretation

When we look at the matrix graph or the pairwise Pearson correlations table we see that we have six possible pairwise combinations (every possible pairing of the four variables). Let's say we wanted to examine the relationship between exercise and height. We would find the row in the pairwise Pearson correlations table where these two variables are listed for sample 1 and sample 2. In this case, that is the first row. The correlation between exercise and height is 0.118 and the p-value is 0.026.

If we were conducting a hypothesis test for this relationship, these would be step 2 and 3 in the 5 step process.