A student-run cafe wants to use data to determine how many wraps they should make today. If they make too many wraps they will have waste. But, if they don't make enough wraps they will lose out on potential profit. They have been collecting data concerning their daily sales as well as data concerning the daily temperature. They found that there is a statistically significant relationship between daily temperature and coffee sales. So, the students want to know if a similar relationship exists between daily temperature and wrap sales. The video below will walk you through the process of using simple linear regression to determine if the daily temperature can be used to predict wrap sales. The screenshots and annotation below the video will walk you through these steps again.
Can daily temperature be used to predict wrap sales?
Data concerning sales at a student-run cafe were obtained from a Journal of Statistics Education article. Data were retrieved from cafedata.xls more information about this data set available at cafedata.txt.
For the analysis you can use the Minitab file: cafedata.mpx
- \(H_0\colon \beta_1 =0\)
- \(H_a\colon \beta_1 \neq 0\)
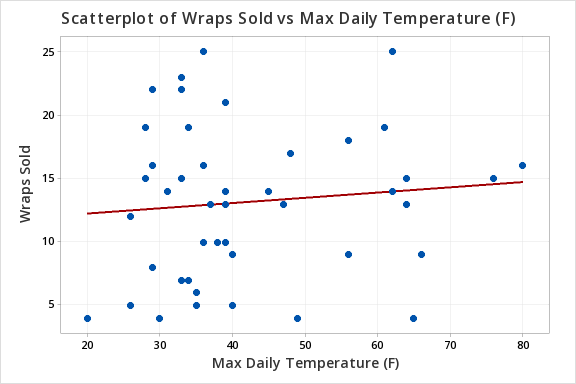
The scatterplot below shows that the relationship between maximum daily temperature and wrap sales is linear (or at least it's not non-linear). Though the relationship appears to be weak.
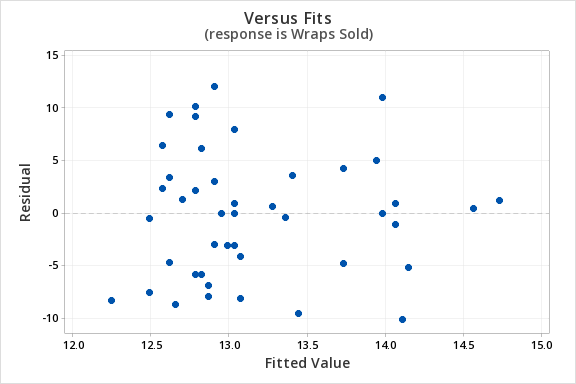
The plot of residuals versus fits below can be used to check the assumptions of independent errors and equal error variances. There is not a significant correlation between the residuals and fits, therefore the assumption of independent errors has been met. The variance of the residuals is relatively consistent for all fitted values, therefore the assumption of equal error variances has been met.
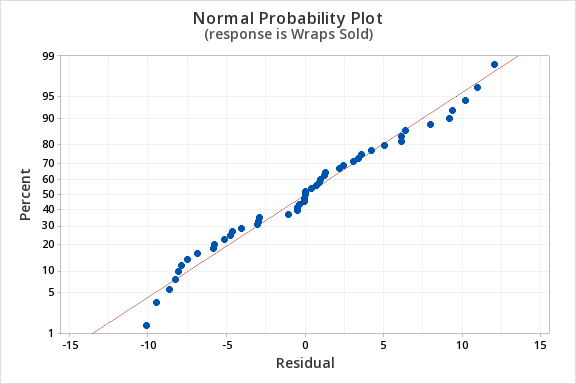
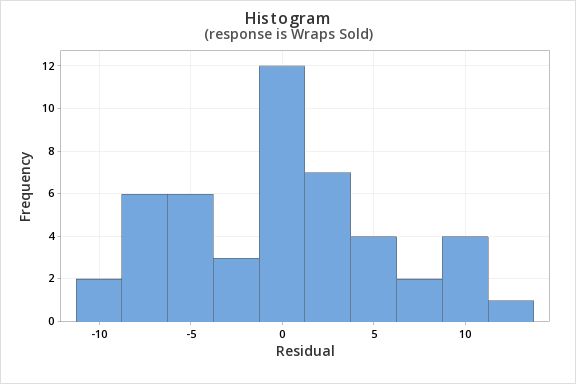
Finally, we must check for the normality of errors. We can use the normal probability plot below to check that our data points fall near the line. Or, we can use the histogram of residuals below to check that the errors are approximately normally distributed.
Now that we have check all of the assumptions of simple linear regression, we can examine the regression model.
Regression Equation
Wraps Sold = 11.42 + 0.0414 Max Daily Temperature (F)
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 11.42 | 2.66 | 4.29 | 0.000 | |
| Max Daily Temperature (F) | 0.0414 | 0.0603 | 0.69 | 0.496 | 1.00 |
Model Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 5.90208 | 1.04% | 0.00% | 0.00% |
Analysis of Variance
| Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 1 | 16.41 | 16.41 | 0.47 | 0.496 |
| Max Daily Temperature (F) | 1 | 16.41 | 16.41 | 0.47 | 0.496 |
| Error | 45 | 1567.55 | 34.83 | ||
| Lack-of-Fit | 24 | 875.17 | 36.47 | 1.11 | 0.411 |
| Pure Error | 21 | 692.38 | 32.97 | ||
| Total | 46 | 1583.96 |
\(t = 0.69\)
\(p=0.496\)
\(p > \alpha\), fail to reject the null hypothesis
There is not enough evidence to conclude that maximum daily temperature can be used to predict the number of wraps sold in the population of all days.