Example: Ice Cream Section
The Creamery wants to compare adults and children in terms of preference for eating their ice cream out of a cone. They take a representative sample of 500 customers (240 adults and 260 children) and ask if they prefer cones over bowls. They found that 124 adults preferred cones and 90 children preferred cones.
\(H_0: p_a - p_c = 0\)
\(H_a:p_a - p_c \ne 0\)
Check assumptions:
\(n_a \hat{p}_a = 124\)
\(n_a (1-\widehat p_a) = 240 - 124 = 116\)
\(n_c \widehat p_c = 90\)
\(n_c (1-\widehat p_c) = 260-90 = 170\)
These counts are all at least 10 so we can use the normal approximation method.
Pooled Estimate of \(p\)
\(\widehat{p}=\dfrac{\widehat{p}_1n_1+\widehat{p}_2n_2}{n_1+n_2}\)
\(\widehat{p}=\dfrac{124+90}{240+260}=\dfrac{214}{500}=0.428\)
Standard Error of \(\hat{p}\)
\(SE_{0}={\sqrt{\frac{\widehat{p} (1-\widehat{p})}{n_1}+\frac{\widehat{p}(1-\widehat{p})}{n_2}}}=\sqrt{\widehat{p}(1-\widehat{p})\left ( \frac{1}{n_1}+\frac{1}{n_2} \right )}\)
\(SE_{0}=\sqrt{0.428(1-0.428)\left ( \dfrac{1}{240}+\dfrac{1}{260} \right )}=0.04429\)
Test Statistic for Two Independent Proportions
\(z=\dfrac{\widehat{p}_1-\widehat{p}_2}{SE_0}\)
\(z=\dfrac{\dfrac{124}{240}-\dfrac{90}{260}}{0.04429}=3.850\)
This is a two-tailed test. Our p-value will be the area of the \(z\) distribution more extreme than \(3.850\).
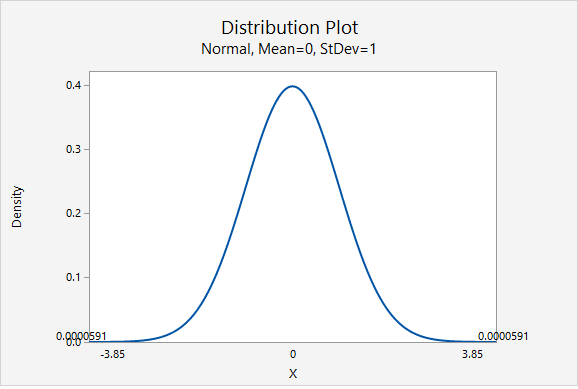
\(p = 0.0000591 \times 2 = 0.0001182\)
\(p \le 0.05\)
Reject the null hypothesis
There is convincing evidence that, in the population of Creamery customers, the proportion of adults who prefer cones is different from the proportion of children who prefer cones in the population.