For the following procedures, the assumption is that both \(np \geq 10\) and \(n(1-p) \geq 10\). When we're constructing confidence intervals \(p\) is typically unknown, in which case we use \(\widehat{p}\) as an estimate of \(p\).
Note that \(n \widehat p\) is the number of successes in the sample and \(n(1- \widehat p)\) is the number of failures in the sample.
This means that our sample needs to have at least 10 "successes" and at least 10 "failures" in order to construct a confidence interval using the normal approximation method.
Below is the general form of a confidence interval.
- General Form of Confidence Interval
- \(sample\ statistic\pm\underbrace{(multiplier)\ (standard\ error)}_{\textbf{margin of error}}\)
The sample statistic here is the sample proportion, \(\widehat p\). When using the normal approximation method the multiplier is taken from the standard normal distribution (i.e., z distribution). And, the standard error is computed using \(\widehat p\) as an estimate of \(p\): \(\sqrt{\frac{\hat{p} (1-\hat{p})}{n}}\). This leaves us with the following formula to construct a confidence interval for a population proportion:
- Confidence Interval of \(p\): Normal Approximation Method
- \(\underbrace{\widehat{p}}_{\text{sample statistic}} \pm \overbrace{z^{*}}^{\text{multiplier}} \underbrace{\left (\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\right)}_{\text{standard error}} \)
Finding the z* Multiplier Section
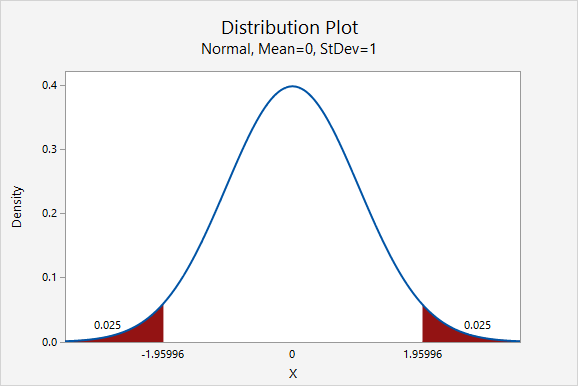
The value of the \(z^*\) multiplier depends on the level of confidence. The multiplier for the confidence interval for a population proportion can be found using the standard normal distribution [i.e., z distribution, N(0,1)]. The most commonly used level of confidence is 95%. As shown on the probability distribution plot below, the multiplier associated with a 95% confidence interval is 1.960, often rounded to 2 (recall the Empirical Rule and 95% Rule).
Below is a table of frequently used \(z^*\) multipliers.
| Confidence Level | \(z^*\) Multiplier |
|---|---|
| 90% | 1.645 |
| 95% | 1.960, often rounded to 2 |
| 98% | 2.327 |
| 99% | 2.576 |
The value of the multiplier increases as the confidence level increases. This leads to wider intervals for higher confidence levels. We are more confident of catching the population value when we use a wider interval.