Sodium Content: HT for One Sample Mean Section
A nutritionist is conducting a study on the sodium content in fast food. They have collected a random sample of 50 different fast-food items from several popular fast-food chains, including burgers, fries, salads, and sandwiches. For each item, the sodium content (in milligrams) is recorded.
The Dietary Guidelines for Americans recommend that adults limit their sodium intake to less than 2300 mg per day. By examining the sodium content in these fast-food items, the nutritionist aims to provide more informed dietary information to their clients so that they can make healthier choices based on the sodium levels found in popular fast foods.
Research Question: Is the average sodium content in a single fast-food item more than 50% of the recommended daily intake of sodium?
Data: FF_sodium.csv
This research question is asking if there is sufficient evidence that the average sodium content in a single fast food item is more than 1150 mg (50% of 2300).
Step 1: We can translate this to the following hypotheses:
\(H_0: \mu=1150 \text{ mg}\)
\(H_a: \mu \gt 1150 \text{ mg}\)
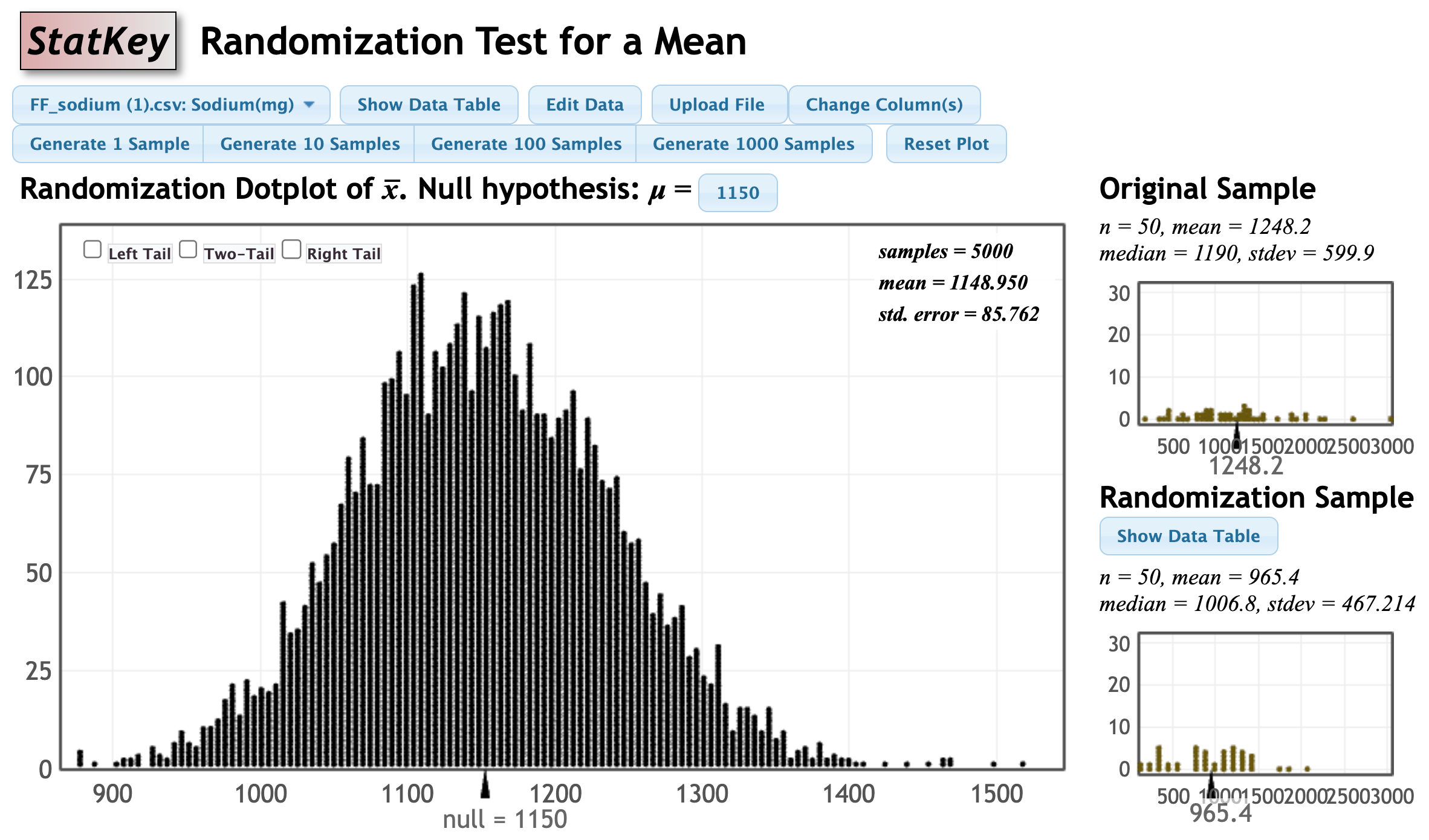
Step 2: Construct a randomization distribution.
- From the StatKey home page choose 'Test for Single Mean.'
- Upload the data set and choose the 'Sodium' variable.
- Change the null value to 1150.
Generate 5,000 randomization samples
Step 3: Find the p-value
- Select 'right tail' in the randomization distribution.
- Change the cutoff value on the x-axis to the sample mean of 1248.2.
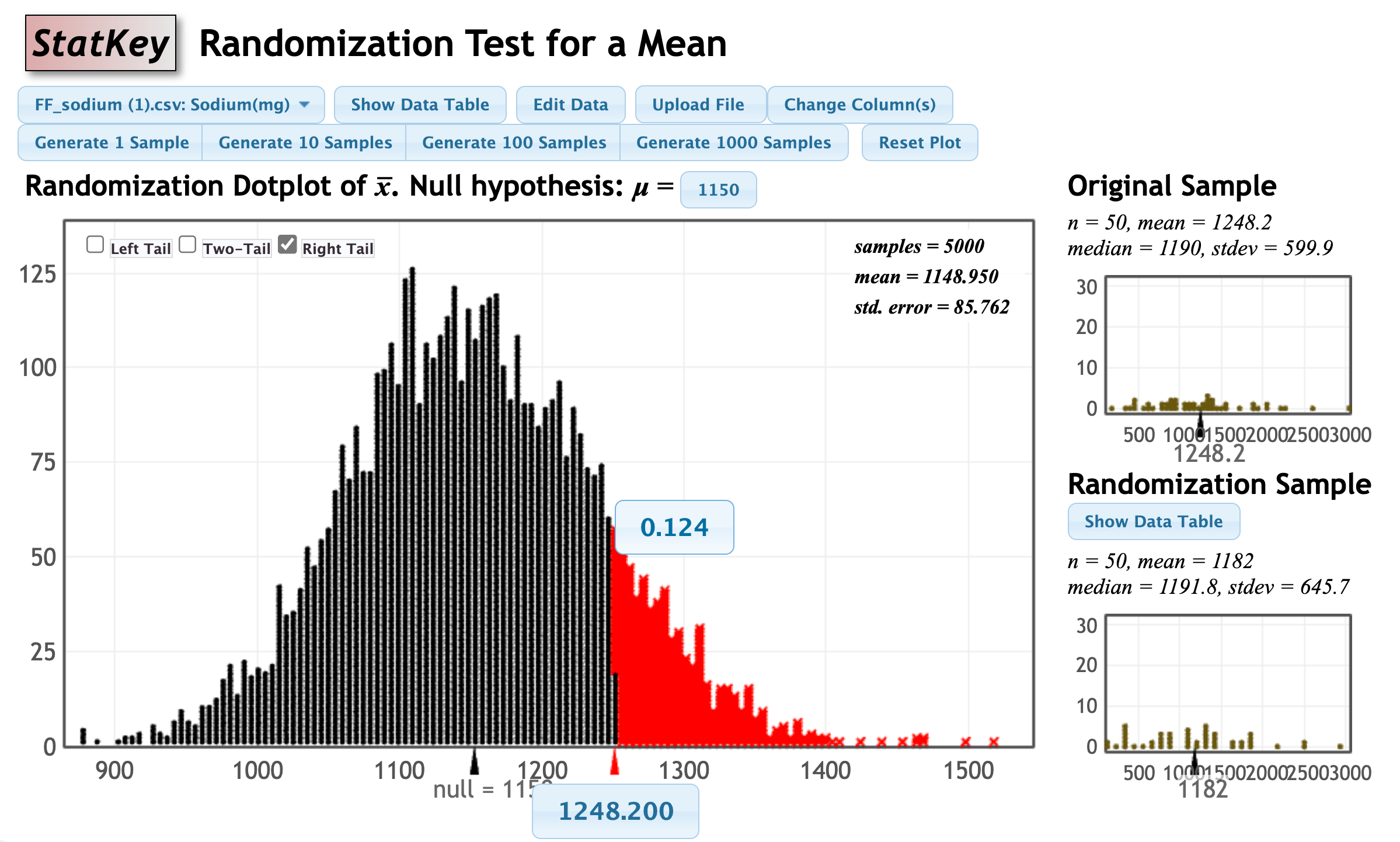
The p-value is 0.124.
Step 4: Make a decision.
Since the p-value is greater than our significance level (\(\alpha=0.05\)), then we fail to reject the null.
Step 5: State a real-world conclusion.
We do not have sufficient evidence that a the average sodium content in a single fast food item is more than 50% of the recommended daily allowance of 2300 mg of sodium.