Let's take a look at some examples so we can get some practice interpreting the coefficient of determination \(R^{2}\) and the correlation coefficient r.
Example 1-1: Temperature in Celsius and Fahrenheit Section
How strong is the linear relationship between temperatures in Celsius and temperatures in Fahrenheit? Here's a plot of an estimated regression equation based on n = 11 data points:
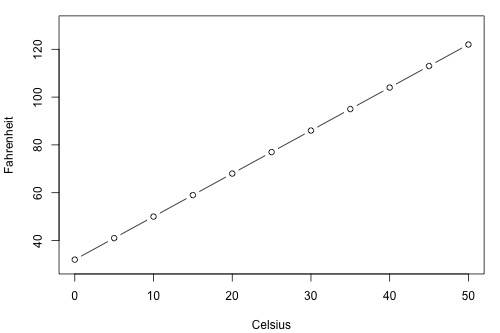
It shouldn't be surprising that Minitab reports that \(R^{2}\) = 100% and r = 1.000. Both measures tell us that there is a perfect linear relationship between temperature in degrees Celsius and temperature in degrees Fahrenheit. We know that the relationship is perfect, namely that Fahrenheit = 32 + 1.8 × Celsius. It should be no surprise then that \(R^{2}\) tells us that 100% of the variation in temperatures in Fahrenheit is explained by the temperature in Celsius.
Example 1-2: Building Stories and Height Section
How strong is the linear relationship between the number of stories a building has and its height? One would think that as the number of stories increases, the height would increase, but not perfectly. Some statisticians compiled data on a set of n = 60 buildings reported in the 1994 World Almanac (Building Stories data). Minitab's fitted line plot and correlation output look like this:
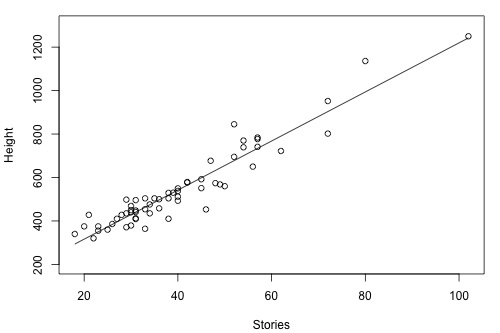
Minitab reports that \(R^{2} = 90.4\%\) and r = 0.951. The positive sign of r tells us that the relationship is positive — as the number of stories increases, height increases — as we expected. Because r is close to 1, it tells us that the linear relationship is very strong, but not perfect. The \(R^{2}\) value tells us that 90.4% of the variation in the height of the building is explained by the number of stories in the building.
Example 1-3: Drivers and Age Section
How strong is the linear relationship between the age of a driver and the distance the driver can see? If we had to guess, we might think that the relationship is negative — as age increases, the distance decreases. A research firm (Last Resource, Inc., Bellefonte, PA) collected data on a sample of n = 30 drivers (Driver Age and Distance data). Minitab's fitted line plot and correlation output on the data looks like this:
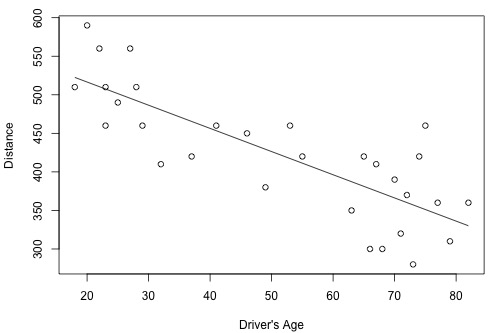
Minitab reports that \(R^{2} = 64.2\%\) and r = -0.801. The negative sign of r tells us that the relationship is negative — as driving age increases, seeing distance decreases — as we expected. Because r is fairly close to -1, it tells us that the linear relationship is fairly strong, but not perfect. The \(R^{2}\) value tells us that 64.2% of the variation in the seeing distance is reduced by taking into account the age of the driver.
Example 1-4: Height and GPA Section
How strong is the linear relationship between the height of a student and his or her grade point average? Data were collected on a random sample of n = 35 students in a statistics course at Penn State University (Height and GPA data ) and the resulting fitted line plot and correlation output were obtained:
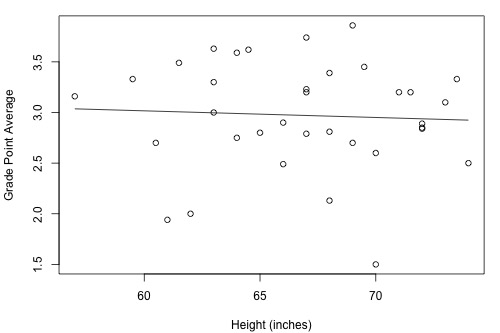
Minitab reports that \(R^{2} = 0.3\% \) and r = -0.053. Because r is quite close to 0, it suggests — not surprisingly, I hope — that there is next to no linear relationship between height and grade point average. Indeed, the \(R^{2}\) value tells us that only 0.3% of the variation in the grade point averages of the students in the sample can be explained by their height. In short, we would need to identify another more important variable, such as the number of hours studied, if predicting a student's grade point average is important to us.