Example 11-7: Male Foot Length and Height Data Section
First, let us consider a dataset where y = foot length (cm) and x = height (in) for n = 33 male students in a statistics class (Height Foot data set).
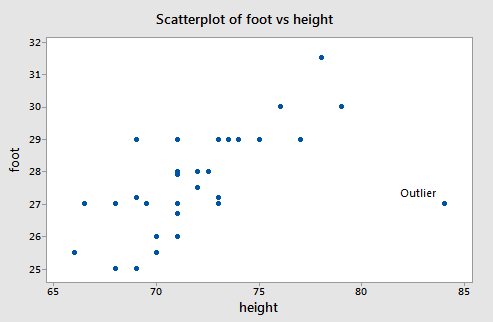
There is a clear outlier with values (\(x_i\) , \(y_i\)) = (84, 27). If that data point is deleted from the dataset, the estimated equation, using the other 32 data points, is \(\hat{y}_i = 0.253 + 0.384x_i\). For the deleted observation, \(x_i\) = 84, so
\(\hat{y}_{i(i)}= 0.253 + 0.384(84) = 32.5093\)
The (unstandardized) deleted residual is
\(d_i=y_i-\hat{y}_{i(i)}= 27 − 32.5093 = −5.5093\)
The usual sample residual will be smaller in absolute size because the outlier will pull the line toward itself. With all data points used, \(\hat{y}_i = 10.936+0.2344x_i\). At \(x_i\) = 84, \(\hat{y}_i = 30.5447\) and \(e_i\) = 27 − 30.5447 = −3.5447.
The difference between the two predicted values computed for the outlier is:
unstandardized \(DFFITS = \hat{y}_i -\hat{y}_{i(i)}= 30.5447 − 32.5093 = −1.9646\).
A dot plot of Cook’s \(D_i\) values for the male foot length and height data is below:
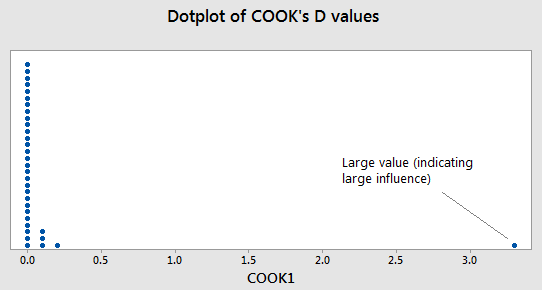
Note the outlier from earlier is the large value way to the right. The one large value of Cook’s \(D_i\) is for the point that is the outlier in the original data set. The interpretation is that the inclusion (or deletion) of this point will have a large influence on the overall results (which we saw from the calculations earlier).
From the analysis we did on the residuals, one may justify deleting the data point (\(x_i\), \(y_i\)) = (84, 27) from the dataset. If you choose to take such a measure in practice, you need to always justify with some sort of residual analysis why you are deleting a data point.
Example 11-8: Hospital Infection Data Section
Below is a scatterplot for the Hospital Infection risk data.
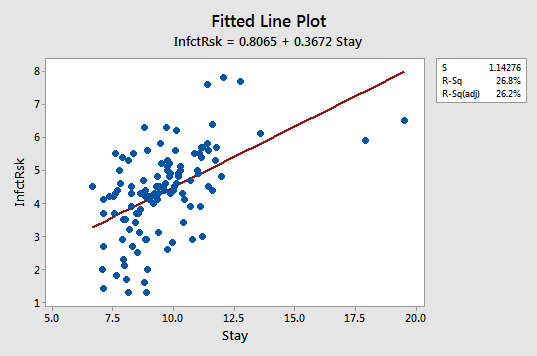
For this dataset, y = infection risk and x = average length of patient stay for n = 112 hospitals in the United States. A regression line is superimposed. Notice that there are two hospitals with extremely large values for the length of stay and that the infection risks for those two hospitals are not correspondingly large. This causes the sample regression line to tilt toward the outliers and apparently not have the correct slope for the bulk of the data.
Below is the “Unusual Observations” display that Minitab gave for this regression.
Fits and Diagnostics for Unusual Observations
| Obs | InfectRsk | Fit | SE Fit | 95% CI | Resid | Std Resid | Del Resid | DFITS | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1.600 | 4.045 | 0.117 | (3.812, 4.277) | -2.445 | -2.15 | -2.19 | -0.225615 | R | |
| 40 | 1.300 | 3.802 | 0.137 | (3.532, 4.073) | -2.502 | -2.21 | -2.25 | -0.270620 | R | |
| 47 | 6.500 | 7.988 | 0.585 | (6.828, 9.148) | -1.488 | -1.52 | -1.53 | -0.909869 | X | |
| 53 | 7.600 | 4.996 | 0.150 | (4.699, 5.293) | 2.604 | 2.30 | 2.35 | 0.310508 | R | |
| 54 | 7.800 | 5.238 | 0.179 | (4.884, 5.592) | 2.562 | 2.27 | 2.31 | 0.366190 | R | |
| 93 | 1.300 | 4.082 | 0.115 | (3.853, 4.310) | -2.782 | -2.55 | -2.50 | -0.253571 | R | |
| 111 | 5.900 | 7.393 | 0.494 | (6.415, 8.372) | -1.493 | -1.45 | -1.46 | -0.697504 | X | |
Click the Results tab in the regression dialog and change “Basic tables” to “Expanded tables” to obtain the additional columns in this table."
Notice that two observations in this display are marked with an 'X'. These are the hospitals with the long average length of stay. Notice also that these two points do not have particularly large studentized residuals (which Minitab calls standardized residuals). This is because the line was "pulled" toward the observed y-values and so the studentized residuals are not overly large. Also, these two points do not have particularly large studentized deleted residuals ("Del Resid"). This is because deleted residuals only adjust for one observation being omitted from the model at a time. In this case, if Obs 47 is omitted, Obs 111 remains to "pull" the regression line towards its observed y-value. Similarly, if Obs 111 is omitted, Obs 47 remains to "pull" the regression line towards its observed y-value. Thus, the deleted residuals are unable to flag that these two observations are probably outliers.
There are five observations marked with an 'R' for "large (studentized) residual." This is about the right number for a sample of n = 112 (5% of 112 comes to 5.6 observations) and none of these studentized residuals are overly large (say, greater than 3 in absolute value). Thus, the two data points to the far right are probably the only ones we need to worry about.
The question here would be whether we should delete the two hospitals to the far right and continue to use a linear model or whether we should retain the hospitals and use a curved model. The justification for deletion might be that we could limit our analysis to hospitals for which length of stay is less than 14 days, so we have a well defined criterion for the dataset that we use.