Recall that structural multicollinearity is multicollinearity that is a mathematical artifact caused by creating new predictors from other predictors, such as, creating the predictor \(x^{2}\) from the predictor x. Because of this, at the same time that we learn here about reducing structural multicollinearity, we learn more about polynomial regression models.
Example 12-4 Section
What is the impact of exercise on the human immune system? To answer this very global and general research question, one has to first quantify what "exercise" means and what "immunity" means. Of course, there are several ways of doing so. For example, we might quantify one's level of exercise by measuring his or her "maximal oxygen uptake." And, we might quantify the quality of one's immune system by measuring the amount of "immunoglobin in his or her blood." In doing so, the general research question is translated into a much more specific research question: "How is the amount of immunoglobin in the blood (y) related to maximal oxygen uptake (x)?"
Because some researchers were interested in answering the above research question, they collected the following Exercise and Immunity data set on a sample of 30 individuals:
- \(y_i\) = amount of immunoglobin in the blood (mg) of individual i
- \(x_i\) = maximal oxygen uptake (ml/kg) of individual i
The scatter plot of the resulting data:
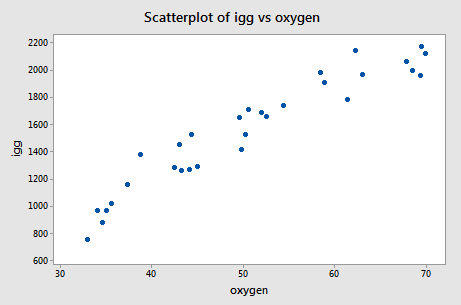
suggests that there might be some curvature to the trend in the data. To allow for the apparent curvature — rather than formulating a linear regression function — the researchers formulated the following quadratic (polynomial) regression function:
\(y_i=\beta_0+\beta_1x_i+\beta_{11}x_{i}^{2}+\epsilon_i\)
where:
- \(y_i\) = amount of immunoglobin in the blood (mg) of individual i
- \(x_i\) = maximal oxygen uptake (ml/kg) of individual i
As usual, the error terms \(\epsilon_i\) are assumed to be independent, normally distributed, and have equal variance \(\sigma^{2}\).
As the following plot of the estimated quadratic function suggests:
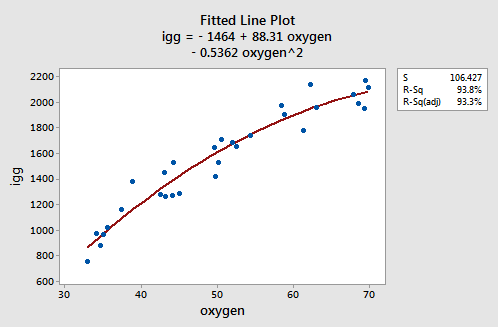
the formulated regression function appears to describe the trend in the data well. The adjusted \(R^{2} \text{-value}\) is 93.3%.
But, now what do the estimated coefficients tell us? The interpretation of the regression coefficients is mostly geometric in nature. That is, the coefficients tell us a little bit about what the picture looks like:
- If 0 is a possible x value, then \(b_0\) is the predicted response when x = 0. Otherwise, the interpretation of \(b_0\) is meaningless.
- The estimated coefficient \(b_1\) is the estimated slope of the tangent line at x = 0.
- The estimated coefficient \(b_2\) indicates the up/down direction of the curve. That is:
- if \(b_2\) < 0, then the curve is concave down
- if \(b_2\) > 0, then the curve is concave up
So far, we have kept our heads a little bit in the sand! If we look at the output we obtain upon regressing the response y = igg on the predictors oxygen and \(\text{oxygen}^{2}\):
Analysis of Variance
| Source | DF | Seq SS | Seq MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 2 | 4602211 | 2301105 | 203.16 | 0.000 |
| oxygen | 1 | 4472047 | 4472047 | 394.83 | 0.000 |
| oxygensq | 1 | 130164 | 130164 | 11.49 | 0.002 |
| Error | 27 | 305818 | 11327 | ||
| Total | 29 | 4908029 |
Modal Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 106.427 | 93.77% | 93.31% | 92.48% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | -1464 | 411 | -3.56 | 0.001 | |
| oxygen | 88.3 | 16.5 | 5.36 | 0.000 | 99.94 |
| oxygensq | -0.536 | 0.158 | -3.39 | 0.002 | 99.94 |
we quickly see that the variance inflation factors for both predictors — oxygen, and oxygensq — are very large (99.9 in each case). Is this surprising to you? If you think about it, we've created a correlation by taking the predictor oxygen and squaring it to obtain oxygensq. That is, just by the nature of our model, we have created a "structural multicollinearity."
The scatter plot of oxygensq versus oxygen:
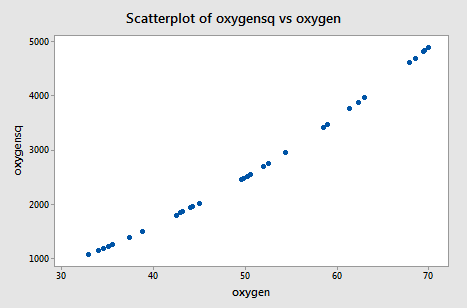
Pearson correlation of oxygen and oxygensq = 0.995
illustrates the intense strength of the correlation that we induced. After all, we just can't get much more correlated than a correlation of r = 0.995!
The neat thing here is that we can reduce the multicollinearity in our data by doing what is known as "centering the predictors." Centering a predictor merely entails subtracting the mean of the predictor values in the data set from each predictor value. For example, Minitab reports that the mean of the oxygen values in our data set is 50.64:
Descriptive Statistics: oxygen
| Variable | N | N* | Mean | SE Mean | StDev | Minimum | Q1 | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|---|---|---|---|
| oxygen | 30 | 0 | 50.64 | 2.19 | 11.99 | 33.00 | 41.58 | 50.00 | 61.63 | 69.90 |
Therefore, to center the predictor oxygen, we merely subtract 50.64 from each oxygen value in our data set. Doing so, we obtain the centered predictor, oxcent, say:
| oxygen | oxcent | oxcentsq |
|---|---|---|
| 34.6 | -16.04 | 257.282 |
| 45.0 | -5.64 | 31.810 |
| 62.3 | 11.66 | 135.956 |
| 58.9 | 8.26 | 68.228 |
| 42.5 | -8.14 | 66.260 |
| 44.3 | -6.34 | 40.196 |
| 67.9 | 17.26 | 297.908 |
| 58.5 | 7.86 | 61.780 |
| 35.6 | -15.04 | 226.202 |
| 49.6 | -1.04 | 1.082 |
| 33.0 | -17.64 | 311.170 |
For example, 34.6 minus 50.64 is -16.04, and 45.0 minus 50.64 is -5.64, and so on. Now, to include the squared oxygen term in our regression model — to allow for curvature in the trend — we square the centered predictor oxcent to obtain oxcentsq. That is, \(\left(-16.04\right)^{2} = 257.282\) and \(\left(-5.64\right)^{2} = 31.810\), and so on.
Wow! It really works! The scatter plot of oxcentsq versus oxcent:
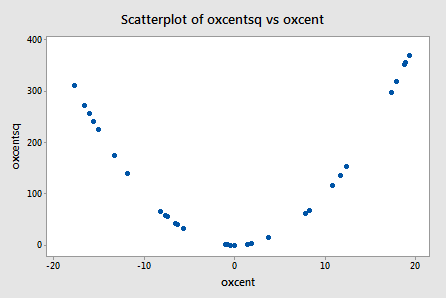
Pearson correlation of oxcent and oxygensq = 0.219
illustrates — by centering the predictors — just how much we've reduced the correlation between the predictor and its square. The correlation has gone from a whopping r = 0.995 to a rather low r = 0.219!
Having centered the predictor oxygen, we must reformulate our quadratic polynomial regression model accordingly. That is, we now formulate our model as:
\(y_i=\beta_{0}^{*}+\beta_{1}^{*}(x_i-\bar{x})+\beta_{11}^{*}(x_i-\bar{x})^{2}+\epsilon_i\)
or alternatively:
\(y_i=\beta_{0}^{*}+\beta_{1}^{*}x_{i}^{*}+\beta_{11}^{*}x_{i}^{*2}+\epsilon_i\)
where:
- \(y_i\) = amount of immunoglobin in the blood (mg), and
- \(x_{i}^{*}=x_i-\bar{x}\) denotes the centered predictor
and the error terms \(\epsilon_i\) are independent, normally distributed and have equal variance \(\sigma^{2}\). Note that we add asterisks to each of the parameters to make it clear that the parameters differ from the parameters in the original model we formulated.
Let's see how we did by centering the predictors and reformulating our model. Recall that — based on our original model — the variance inflation factors for oxygen and oxygensq were 99.9. Now, regressing y = igg on the centered predictors oxcent and oxcentsq:
Analysis of Variance
| Source | DF | Seq SS | Seq MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Regression | 2 | 4602211 | 2301105 | 203.16 | 0.000 |
| oxygen | 1 | 4472047 | 4472047 | 394.83 | 0.000 |
| oxygensq | 1 | 130164 | 130164 | 11.49 | 0.002 |
| Error | 27 | 305818 | 11327 | ||
| Total | 29 | 4908029 |
Modal Summary
| S | R-sq | R-sq(adj) | R-sq(pred) |
|---|---|---|---|
| 106.427 | 93.77% | 93.31% | 92.48% |
Coefficients
| Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 1632.3 | 29.3 | 55.62 | 0.000 | |
| oxygen | 34.00 | 1.69 | 20.13 | 0.000 | 1.05 |
| oxygensq | -0.536 | 0.158 | -3.39 | 0.002 | 1.05 |
we see that the variance inflation factors have dropped significantly — now they are 1.05 in each case.
Because we reformulated our model based on the centered predictors, the meaning of the parameters must be changed accordingly. Now, the estimated coefficients tell us:
- The estimated coefficient \(b_0\) is the predicted response y when the predictor x equals the sample mean of the predictor values.
- The estimated coefficient \(b_1\) is the estimated slope of the tangent line at the predictor mean — and, often, it is similar to the estimated slope in the simple linear regression model.
- The estimated coefficient \(b_2\) indicates the up/down direction of the curve. That is:
- if \(b_2\) < 0, then the curve is concave down
- if \(b_2\) > 0, then the curve is concave up
So, here, in this example, the estimated coefficient \(b_0\) = 1632.3 tells us that a male whose maximal oxygen uptake is 50.64 ml/kg is predicted to have 1632.3 mg of immunoglobin in his blood. And, the estimated coefficient \(b_1\) = 34.00 tells us that when an individual's maximal oxygen uptake is near 50.64 ml/kg, we can expect the individual's immunoglobin to increase by 34.00 mg for every 1 ml/kg increase in maximal oxygen uptake.
As the following plot of the estimated quadratic function suggests:
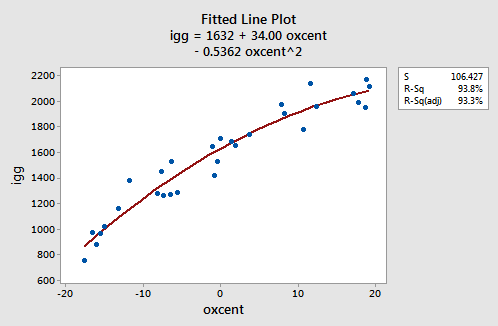
the reformulated regression function appears to describe the trend in the data well. The adjusted \(R^{2} \text{-value}\) is still 93.3%.
We shouldn't be surprised to see that the estimates of the coefficients in our reformulated polynomial regression model are quite similar to the estimates of the coefficients for the simple linear regression model:
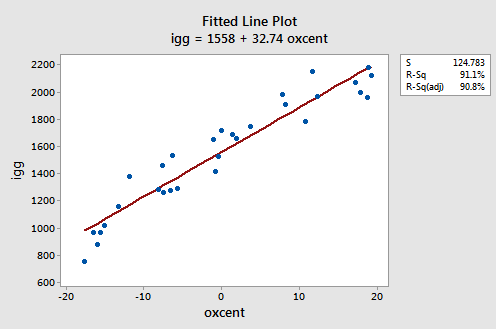
As you can see, the estimated coefficient \(b_1\) = 34.00 for the polynomial regression model and \(b_1\) = 32.74 for the simple linear regression model. And, the estimated coefficient \(b_0\) = 1632 for the polynomial regression model and \(b_0\) = 1558 for the simple linear regression model. The similarities in the estimates, of course, arise from the fact that the predictors are nearly uncorrelated and therefore the estimates of the coefficients don't change all that much from model to model.
Now, you might be getting this sense that we're "mucking around with the data" to get an answer to our research questions. One way to convince you that we're not is to show you that the two estimated models are algebraically equivalent. That is, if given one form of the estimated model, say the estimated model with the centered predictors:
\(y_i=b_{0}^{*}+b_{1}^{*}x_{i}^{*}+b_{11}^{*}x_{i}^{*2}\)
then, the other form of the estimated model, say the estimated model with the original predictors:
\(y_i=b_{0}+b_{1}x_{i}+b_{11}x_{i}^{2}\)
can be easily obtained. In fact, it can be shown algebraically that the estimated coefficients of the original model equal:
\(\begin{align}
b_{0}&=b_{0}^{*}-b_{1}^{*}\bar{x}+b_{11}^{*}\bar{x}^{2}\\
b_{1}&= b_{1}^{*}-2b_{11}^{*}\bar{x}\\
b_{11}&= b_{11}^{*}\\
\end{align}\)
For example, the estimated regression function for our reformulated model with centered predictors is:
\(\hat{y}_i=1632.3+34.00x_{i}^{*}-0.536x_{i}^{*2}\)
Then, since the mean of the oxygen values in the data set is 50.64:
Descriptive Statistics: oxygen
| Variable | N | N* | Mean | SE Mean | StDev | Minimum | Q1 | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|---|---|---|---|
| oxygen | 30 | 0 | 50.64 | 2.19 | 11.99 | 33.00 | 41.58 | 50.00 | 61.63 | 69.90 |
it can be shown algebraically that the estimated coefficients for the model with the original (uncentered) predictors are:
\(b_0 = 1632.3 - 34.00(50.64) - 0.536(50.64)^{2} = -1464\)
\(b_1 = 34.00 - 2(- 0.536)(50.64) = 88.3\)
\(b_{11} = - 0.536\)
That is, the estimated regression function for our quadratic polynomial model with the original (uncentered) predictors is:
\(\hat{y}_i=-1464+88.3x_{i}-0.536x_{i}^{2}\)
Given the equivalence of the two estimated models, you might ask why we bother to center the predictors. The main reason for centering to correct structural multicollinearity is that low levels of multicollinearity can help avoid computational inaccuracies. Specifically, a near-zero determinant of \(X^{T}X\) is a potential source of serious roundoff errors in the calculations of the normal equations. Severe multicollinearity has the effect of making this determinant come close to zero. Thus, under severe multicollinearity, the regression coefficients may be subject to large roundoff errors.
Let's use our model to predict the immunoglobin level in the blood of a person whose maximal oxygen uptake is 90 ml/kg. Of course, before we use our model to answer a research question, we should always evaluate it first to make sure it means all of the necessary conditions. The residuals versus fits plot:
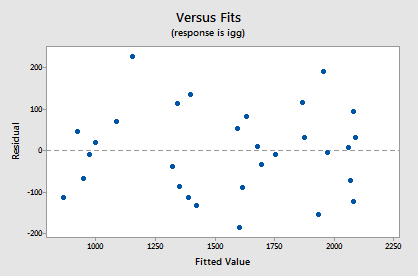
shows a nice horizontal band around the residual = 0 line, suggesting the model fits the data well. It also suggests that the variances of the error terms are equal. And, the normal probability plot:
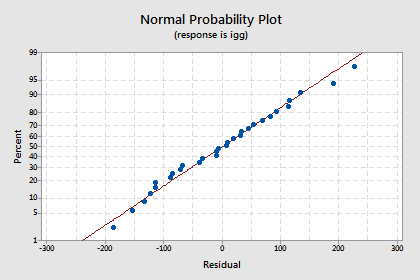
suggests that the error terms are normally distributed. Okay, we're good to go — let's use the model to answer our research question: "What is one's predicted IgG if the maximal oxygen uptake is 90 ml/kg?"
When asking Minitab to make this prediction, you have to remember that we have centered the predictors. That is, if oxygen = 90, then oxcent = 90-50.64 = 39.36. And, if oxcent = 39.36, then oxcentsq = 1549.210. Asking Minitab to predict the igg of an individual whose oxcent = 39.4 and oxcentsq = 1549, we obtain the following output:
Regression Equation
\(\widehat{igg} = 1632.3 + 34.00 oxcent - 0.536 oxcentsq\)
| variable | Setting |
|---|---|
| oxcent | 39.4 |
| oxcentsq | 1549 |
| Fit | SE Fit | 95% CI | 95% PI | |
|---|---|---|---|---|
| 2141.10 | 219.209 | (1691.32, 2590.88) | (1641.12, 2641.09) | XX |
XX denotes an extremely unusual point relative to predictor levels used to fit the model
Why does Minitab report that "XX denotes a row with very extreme X values?" Recall that the levels of maximal oxygen uptake in the data set ranged from 30 to 70 ml/kg. Therefore, a maximal oxygen uptake of 90 is way outside the scope of the model, and Minitab provides such a warning.
A word of warning. Be careful — because of changes in direction of the curve, there is an even greater danger of extrapolation when modeling data with a polynomial function.
The hierarchical approach to model fitting Section
Just one closing comment since we've been discussing polynomial regression to remind you about the "hierarchical approach to model fitting." The widely accepted approach to fitting polynomial regression functions is to fit a higher-order model and then explore whether a lower-order (simpler) model is adequate. For example, suppose we formulate the following cubic polynomial regression function:
\(y_i=\beta_{0}+\beta_{1}x_{i}+\beta_{11}x_{i}^{2}+\beta_{111}x_{i}^{3}+\epsilon_i\)
Then, to see if the simpler first-order model (a "line") is adequate in describing the trend in the data, we could test the null hypothesis:
\(H_0 \colon \beta_{11}=\beta_{111}=0\)
But then … if a polynomial term of a given order is retained, then all related lower-order terms are also retained. That is, if a quadratic term is deemed significant, then it is standard practice to use this regression function:
\(\mu_Y=\beta_{0}+\beta_{1}x_{i}+\beta_{11}x_{i}^{2}\)
and not this one:
\(\mu_Y=\beta_{0}+\beta_{11}x_{i}^{2}\)
That is, we always fit the terms of a polynomial model in a hierarchical manner.