In this section, we learn how to build and use a model by transforming the response y values. Transforming the y values should be considered when non-normality and/or unequal variances are the problems with the model. As an added bonus, the transformation on y may also help to "straighten out" a curved relationship.
Again, keep in mind that although we're focussing on a simple linear regression model here, the essential ideas apply more generally to multiple linear regression models too.
Example 9-2: Mammal Gestation Section
Building the model
Let's consider data (Mammal Gest Data) on the typical birthweight and length of gestation for various mammals. We treat the birthweight (x, in kg) as the predictor and the length of gestation (y, in the number of days until birth) as the response.
The fitted line plot suggests that the relationship between gestation length (y) and birthweight (x) is linear, but that the variance of the error terms might not be equal:
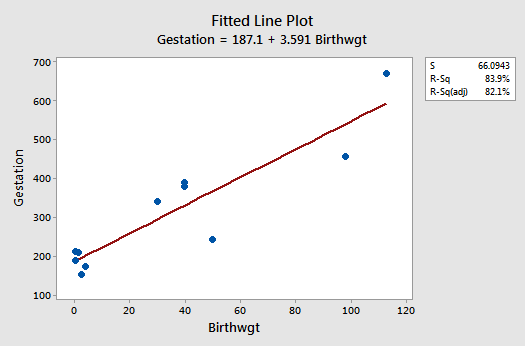
The residuals vs. fits plot exhibits some fanning and therefore provides yet more evidence that the variance of the error terms might not be equal:
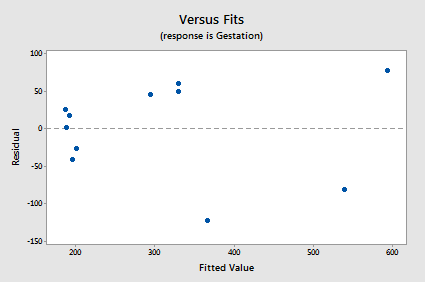
The normal probability plot supports the assumption of normally distributed error terms:
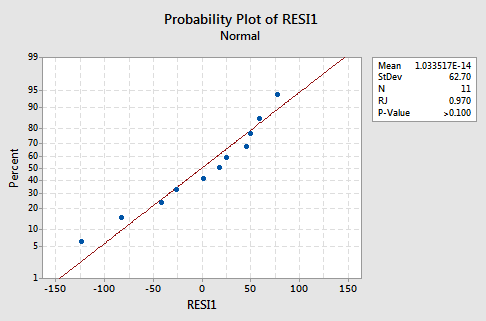
The line is approximately straight and the Ryan-Joiner P-value is large. We fail to reject the null hypothesis of normal error terms. There is not enough evidence to conclude that the error terms are not normal.
Let's transform the y values by taking the natural logarithm of the lengths of gestation. Doing so, we obtain the new response y = lnGest:
| Mammal | Birthwgt | Gestation | lnGest |
|---|---|---|---|
| Goat | 2.75 | 155 | 5.04343 |
| Sheep | 4.00 | 175 | 5.16479 |
| Deer | 0.48 | 190 | 5.24702 |
| Porcupine | 1.50 | 210 | 5.34711 |
| Bear | 0.37 | 213 | 5.36129 |
| Hippo | 50.00 | 243 | 5.49306 |
| Horse | 30.00 | 340 | 5.82895 |
| Camel | 40.00 | 380 | 5.94017 |
| Zebra | 40.00 | 390 | 5.96615 |
| Giraffe | 98.00 | 457 | 6.12468 |
| Elephant | 113.00 | 670 | 6.50728 |
For example, \(ln\left(155\right) = 5.04343\) and \(ln\left(457\right) = 6.12468\). Now that we've transformed the response y values, let's see if it helped rectify the problem with the unequal error variances.
The fitted line plot with y = lnGest as the response and x = Birthwgt as the predictor suggests that the log transformation of the response has helped:
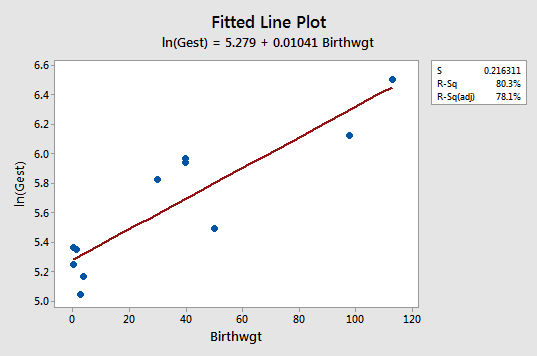
Note that, as expected, the log transformation has tended to "spread out" the smaller gestations and tended to "bring in" the larger ones.
The new residual vs. fits plot shows a marked improvement in the spread of the residuals:
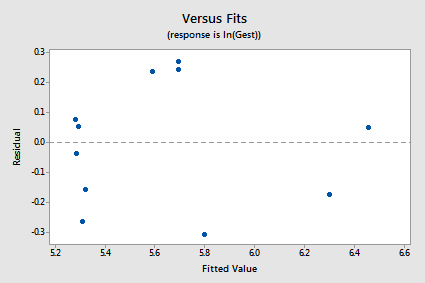
The log transformation of the response did not adversely affect the normality of the error terms:
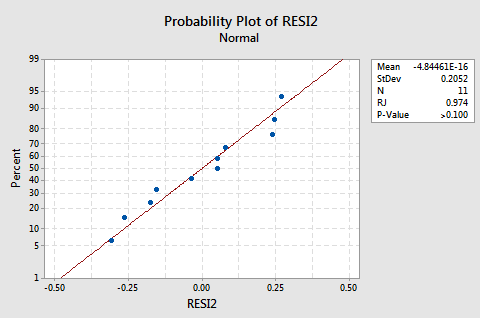
The line is approximately straight and the Ryan-Joiner P-value is large. We fail to reject the null hypothesis of normal error terms. There is not enough evidence to conclude that the error terms are not normal.
Note that the \(r^{2}\) value is lower for the transformed model than for the untransformed model (80.3% versus 83.9%). This does not mean that the untransformed model is preferable. Remember the untransformed model failed to satisfy the equal variance condition, so we should not use this model anyway.
Again, transforming the y values should be considered when non-normality and/or unequal variances are the main problems with the model.
Using the Model
We've identified what we think is the best model for the mammal birthweight and gestation data. The model meets the four "LINE" conditions. Therefore, we can use the model to answer our research questions of interest. We may or may not have to make slight modifications to the standard procedures we've already learned.
Let's use our linear regression model for the mammal birthweight and gestation data — with y = lnGest as the response and x = birthwgt as the predictor — to answer four different research questions.
Research Question #1: What is the nature of the association between mammalian birth weight and length of gestation?

Again, to answer this research question, we just describe the nature of the relationship. That is, the natural logarithm of the length of gestation is positively linearly related to birthweight. That is, as the average birthweight of the mammal increases, the expected natural logarithm of the gestation length also increases.
Research Question #2: Is there an association between mammalian birth weight and length of gestation?
Again, in answering this research question, no modification to the standard procedure is necessary. We merely test the null hypothesis \(H_0 \colon \beta_1 = 0\) using either the F-test or the equivalent t-test:
The regression equation is
\(\widehat{lnGest} = 5.28 + 0.0104 Birthwgt\)
| Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
| Constant | 5.27882 | 0.08818 | 59.87 | 0.000 |
| Birthwgt | 0.010410 | 0.001717 | 6.06 | 0.000 |
| Model Summary | ||
|---|---|---|
| S = 0.2163 | R-Sq = 80.3% | R-Sq(adj) = 78.1% |
Analysis of Variance
| Source | DF | SS | MS | F | P |
|---|---|---|---|---|---|
| Regression | 1 | 1.7193 | 1.7193 | 36.75 | 0.000 |
| Residual Error | 9 | 0.4211 | 0.0468 | ||
| Total | 10 | 2.1405 |
As the Minitab output illustrates, the P-value is < 0.001. There is significant evidence at the 0.05 level to conclude that there is a linear association between the mammalian birthweight and the natural logarithm of the length of gestation.
Research Question #3: What is the expected gestation length of a new 50 kg mammal?
In answering this research question, if we are only interested in obtaining a point estimate, we merely enter x = 50 into the estimated regression equation:
\(ln(\widehat{Gest})=5.28+0.0104 \times Birthwgt\)
to obtain:
\(ln(\widehat{Gest})=5.28+0.0104 \times 50=5.8\)
That is, we predict the length of gestation of a 50 kg mammal to be 5.8 log days! Well, that's not very informative! We need to transform the answer back into the original units. This just requires recalling one of the fundamental properties of the natural logarithm, namely that ex and ln(x) "cancel each other out." That is:
\(\widehat{Gest}=e^{ln(\widehat{Gest})}\)
Furthermore, if we exponentiate the left side of the equation:
\(ln(\widehat{Gest})=5.28+0.0104 \times 50=5.8\)
we also have to exponentiate the right side of the equation. By doing so, we obtain:
\(\widehat{Gest}=e^{ln(\widehat{Gest})}=e^{5.8}=330.3\)
We predict the gestation length of a 50 kg mammal to be 330 days. That sounds better!
Again, a point estimate is of limited usefulness. It doesn't tell us how confident we can be that the prediction is close to the true unknown value. We should calculate a 95% prediction interval. Minitab tells us:
Values of Predictions for New Observations
| New Obs | Birthwgt |
|---|---|
| 1 | 50.0 |
Prediction Values for New Observations
| New | Fit | SE Fit | 95.0% CI | 95.0% PI |
|---|---|---|---|---|
| 1 | 5.7993 | 0.0704 | (5.6401, 5.9586) | (5.2847, 6.3139) |
that we can be 95% confident that the gestation length of a 50 kg mammal is predicted to be between 5.2847 and 6.3139 log days! Again, we need to transform these predicted limits back into the original units. By doing so, we obtain:
\(e^{5.2847} = 197.3\) and \(e^{6.3139} = 552.2\)
We can be 95% confident that the gestation length for a 50 kg mammal will be between 197.3 and 552.2 days.
Research Question #4: What is the expected change in length of gestation for each one-pound increase in birth weight?
Figuring out how to answer this research question takes a little bit of work — and some creativity, too! If you only care about the end result, this is it:
- The median of the response changes by a factor of \(e^{\beta_1}\) for each one unit increase in the predictor x. Although you won't be required to duplicate the derivation, it might help you understand—and therefore remember—the result.
- And, therefore, the median of the response changes by a factor of \(e^{k\beta_1}\) for each k-unit increase in the predictor x. Again, although you won't be required to duplicate the derivation, it might help you understand — and therefore remember — the result.
- As always, we won't know the slope of the population line, \(\beta_1\), so we'll have to use \(b_1\) to estimate it.
For the mammalian birthweight and gestation data, Minitab tells us that \(b_1 = 0.01041 \colon\)
| Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
| Constant | 5.27882 | 0.08818 | 59.87 | 0.000 |
| Birthwgt | 0.010410 | 0.001717 | 6.06 | 0.000 |
and therefore:
\(e^{b_1}=e^{0.010410}=1.01\)
The result tells us that the predicted median gestation changes by a factor of 1.01046 for each one-unit increase in birthweight. For example, the predicted median gestation for a mammal weighing 3 kgs is 1.01046 times the median gestation for a mammal weighing 2 kgs. And, since there is a 10-unit increase going from a 20 kg to a 30 kg mammal, the median gestation for a mammal weighing 30 kgs is \(1.01046^{10} = 1.1097\) times the median gestation for a mammal weighing 20 kgs.
So far, we've only calculated a point estimate for the expected change. Of course, a 95% confidence interval for \(\beta_1\) is:
0.01041 ± 2.2622(0.001717) = (0.0065, 0.0143)
Because:
\(e^{0.0065} = 1.007\) and \(e^{0.0143} = 1.014\)
we can be 95% confident that the median gestation will increase by a factor between 1.007 and 1.014 for each one-kilogram increase in birth weight. And, since:
\(1.007^{10} = 1.072\) and \(1.014^{10} = 1.149\)
we can be 95% confident that the median gestation will increase by a factor between 1.072 and 1.149 for each 10-kilogram increase in birth weight.