In this section, we learn about the stepwise regression procedure. While we will soon learn the finer details, the general idea behind the stepwise regression procedure is that we build our regression model from a set of candidate predictor variables by entering and removing predictors — in a stepwise manner — into our model until there is no justifiable reason to enter or remove any more.
Our hope is, of course, that we end up with a reasonable and useful regression model. There is one sure way of ending up with a model that is certain to be underspecified — and that's if the set of candidate predictor variables doesn't include all of the variables that actually predict the response. This leads us to a fundamental rule of the stepwise regression procedure — the list of candidate predictor variables must include all of the variables that actually predict the response. Otherwise, we are sure to end up with a regression model that is underspecified and therefore misleading.
Example 10-1: Cement Data Section
Let's learn how the stepwise regression procedure works by considering a data set that concerns the hardening of cement. Sounds interesting, eh? In particular, the researchers were interested in learning how the composition of the cement affected the heat that evolved during the hardening of the cement. Therefore, they measured and recorded the following data (Cement dataset) on 13 batches of cement:
- Response \(y \colon \) heat evolved in calories during the hardening of cement on a per gram basis
- Predictor \(x_1 \colon \) % of tricalcium aluminate
- Predictor \(x_2 \colon \) % of tricalcium silicate
- Predictor \(x_3 \colon \) % of tetracalcium alumino ferrite
- Predictor \(x_4 \colon \) % of dicalcium silicate
Now, if you study the scatter plot matrix of the data:
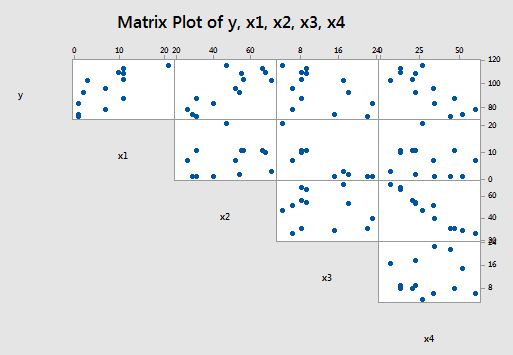
you can get a hunch of which predictors are good candidates for being the first to enter the stepwise model. It looks as if the strongest relationship exists between either \(y\) and \(x_{2} \) or between \(y\) and \(x_{4} \) — and therefore, perhaps either \(x_{2} \) or \(x_{4} \) should enter the stepwise model first. Did you notice what else is going on in this data set though? A strong correlation also exists between the predictors \(x_{2} \) and \(x_{4} \) ! How does this correlation among the predictor variables play out in the stepwise procedure? Let's see what happens when we use the stepwise regression method to find a model that is appropriate for these data.
The procedure
Again, before we learn the finer details, let me again provide a broad overview of the steps involved. First, we start with no predictors in our "stepwise model." Then, at each step along the way we either enter or remove a predictor based on the partial F-tests — that is, the t-tests for the slope parameters — that are obtained. We stop when no more predictors can be justifiably entered or removed from our stepwise model, thereby leading us to a "final model."
Now, let's make this process a bit more concrete. Here goes:
Starting the procedure
The first thing we need to do is set a significance level for deciding when to enter a predictor into the stepwise model. We'll call this the Alpha-to-Enter significance level and will denote it as \(\alpha_{E} \). Of course, we also need to set a significance level for deciding when to remove a predictor from the stepwise model. We'll call this the Alpha-to-Remove significance level and will denote it as \(\alpha_{R} \). That is, first:
- Specify an Alpha-to-Enter significance level. This will typically be greater than the usual 0.05 level so that it is not too difficult to enter predictors into the model. Many software packages — Minitab included — set this significance level by default to \(\alpha_E = 0.15\).
- Specify an Alpha-to-Remove significance level. This will typically be greater than the usual 0.05 level so that it is not too easy to remove predictors from the model. Again, many software packages — Minitab included — set this significance level by default to \(\alpha_{R} = 0.15\).
Step #1:
Once we've specified the starting significance levels, then we:
- Fit each of the one-predictor models — that is, regress \(y\) on \(x_{1} \), regress \(y\) on \(x_{2} \), ..., and regress \(y\) on \(x_{p-1} \).
- Of those predictors whose t-test P-value is less than \(\alpha_E = 0.15\), the first predictor put in the stepwise model is the predictor that has the smallest t-test P-value.
- If no predictor has a t-test P-value less than \(\alpha_E = 0.15\), stop.
Step #2:
Then:
- Suppose \(x_{1} \) had the smallest t-test P-value below \(\alpha_{E} = 0.15\) and therefore was deemed the "best" single predictor arising from the first step.
- Now, fit each of the two-predictor models that include \(x_{1} \) as a predictor — that is, regress \(y\) on \(x_{1} \) and \(x_{2} \) , regress \(y\) on \(x_{1} \) and \(x_{3} \) , ..., and regress \(y\) on \(x_{1} \) and \(x_{p-1} \) .
- Of those predictors whose t-test P-value is less than \(\alpha_E = 0.15\), the second predictor put in the stepwise model is the predictor that has the smallest t-test P-value.
- If no predictor has a t-test P-value less than \(\alpha_E = 0.15\), stop. The model with the one predictor obtained from the first step is your final model.
- But, suppose instead that \(x_{2} \) was deemed the "best" second predictor and it is therefore entered into the stepwise model.
- Now, since \(x_{1} \) was the first predictor in the model, step back and see if entering \(x_{2} \) into the stepwise model somehow affected the significance of the \(x_{1} \) predictor. That is, check the t-test P-value for testing \(\beta_{1}= 0\). If the t-test P-value for \(\beta_{1}= 0\) has become not significant — that is, the P-value is greater than \(\alpha_{R} \) = 0.15 — remove \(x_{1} \) from the stepwise model.
Step #3
Then:
- Suppose both \(x_{1} \) and \(x_{2} \) made it into the two-predictor stepwise model and remained there.
- Now, fit each of the three-predictor models that include \(x_{1} \) and \(x_{2} \) as predictors — that is, regress \(y\) on \(x_{1} \) , \(x_{2} \) , and \(x_{3} \) , regress \(y\) on \(x_{1} \) , \(x_{2} \) , and \(x_{4} \) , ..., and regress \(y\) on \(x_{1} \) , \(x_{2} \) , and \(x_{p-1} \) .
- Of those predictors whose t-test P-value is less than \(\alpha_E = 0.15\), the third predictor put in the stepwise model is the predictor that has the smallest t-test P-value.
- If no predictor has a t-test P-value less than \(\alpha_E = 0.15\), stop. The model containing the two predictors obtained from the second step is your final model.
- But, suppose instead that \(x_{3} \) was deemed the "best" third predictor and it is therefore entered into the stepwise model.
- Now, since \(x_{1} \) and \(x_{2} \) were the first predictors in the model, step back and see if entering \(x_{3} \) into the stepwise model somehow affected the significance of the \(x_{1 } \) and \(x_{2} \) predictors. That is, check the t-test P-values for testing \(\beta_{1} = 0\) and \(\beta_{2} = 0\). If the t-test P-value for either \(\beta_{1} = 0\) or \(\beta_{2} = 0\) has become not significant — that is, the P-value is greater than \(\alpha_{R} = 0.15\) — remove the predictor from the stepwise model.
Stopping the procedure
Continue the steps as described above until adding an additional predictor does not yield a t-test P-value below \(\alpha_E = 0.15\).
Whew! Let's return to our cement data example so we can try out the stepwise procedure as described above.
Back to the example...
To start our stepwise regression procedure, let's set our Alpha-to-Enter significance level at \(\alpha_{E} \) = 0.15, and let's set our Alpha-to-Remove significance level at \(\alpha_{R} = 0.15\). Now, regressing \(y\) on \(x_{1} \) , regressing \(y\) on \(x_{2} \) , regressing \(y\) on \(x_{3} \) , and regressing \(y\) on \(x_{4} \) , we obtain:
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 81.479 | 4.927 | 16.54 | 0.000 |
x1 | 1.8687 | 0.5264 | 3.55 | 0.005 |
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 57.424 | 8.491 | 6.76 | 0.000 |
x2 | 0.7891 | 0.1684 | 4.69 | 0.001 |
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 110.203 | 7.948 | 13.87 | 0.000 |
x3 | -1.2558 | 0.5984 | -2.10 | 0.060 |
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 117.568 | 5.262 | 22.34 | 0.000 |
x4 | -0.7382 | 0.1546 | -4.77 | 0.001 |
Each of the predictors is a candidate to be entered into the stepwise model because each t-test P-value is less than \(\alpha_E = 0.15\). The predictors \(x_{2} \) and \(x_{4} \) tie for having the smallest t-test P-value — it is 0.001 in each case. But note the tie is an artifact of Minitab rounding to three decimal places. The t-statistic for \(x_{4} \) is larger in absolute value than the t-statistic for \(x_{2} \) — 4.77 versus 4.69 — and therefore the P-value for \(x_{4} \) must be smaller. As a result of the first step, we enter \(x_{4} \) into our stepwise model.
Now, following step #2, we fit each of the two-predictor models that include \(x_{4} \) as a predictor — that is, we regress \(y\) on \(x_{4} \) and \(x_{1} \), regress \(y\) on \(x_{4} \) and \(x_{2} \), and regress \(y\) on \(x_{4} \) and \(x_{3} \), obtaining:
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 103.097 | 2.124 | 48.54 | 0.000 |
x4 | -0.61395 | 0.04864 | -12.62 | 0.000 |
x1 | 1.4400 | 0.1384 | 10.40 | 0.000 |
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 94.16 | 56.63 | 1.66 | 0.127 |
x4 | -0.4569 | 0.6960 | -0.66 | 0.526 |
x2 | 0.3109 | 0.7486 | 0.42 | 0.687 |
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 131.282 | 3.275 | 40.09 | 0.000 |
x4 | -0.72460 | 0.07233 | -10.02 | 0.000 |
x3 | -1.1999 | 0.1890 | -6.35 | 0.000 |
The predictor \(x_{2} \) is not eligible for entry into the stepwise model because its t-test P-value (0.687) is greater than \(\alpha_E = 0.15\). The predictors \(x_{1} \) and \(x_{3} \) are candidates because each t-test P-value is less than \(\alpha_{E} \) = 0.15. The predictors \(x_{1} \) and \(x_{3} \) tie for having the smallest t-test P-value — it is < 0.001 in each case. But, again the tie is an artifact of Minitab rounding to three decimal places. The t-statistic for \(x_{1} \) is larger in absolute value than the t-statistic for \(x_{3} \) — 10.40 versus 6.3 5— and therefore the P-value for \(x_{1} \) must be smaller. As a result of the second step, we enter \(x_{1} \) into our stepwise model.
Now, since \(x_{4} \) was the first predictor in the model, we must step back and see if entering \(x_{1} \) into the stepwise model affected the significance of the \(x_{4} \) predictor. It did not — the t-test P-value for testing \(\beta_{1} = 0\) is less than 0.001, and thus smaller than \(\alpha_{R} \) = 0.15. Therefore, we proceed to the third step with both \(x_{1} \) and \(x_{4} \) as predictors in our stepwise model.
Now, following step #3, we fit each of the three-predictor models that include x1 and \(x_{4} \) as predictors — that is, we regress \(y\) on \(x_{4} \), \(x_{1} \), and \(x_{2} \); and we regress \(y\) on \(x_{4} \), \(x_{1} \), and \(x_{3} \), obtaining:
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 71.65 | 14.14 | 5.07 | 0.001 |
x4 | -0.2365 | 0.1733 | -1.37 | 0.205 |
x1 | 1.4519 | 0.1170 | 12.41 | 0.000 |
x2 | 0.4161 | 0.1856 | 2.24 | 0.052 |
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 111.684 | 4.562 | 24.48 | 0.000 |
x4 | -0.64280 | 0.04454 | -14.43 | 0.000 |
x1 | 1.0519 | 0.2237 | 4.70 | 0.001 |
x3 | -0.4100 | 0.1992 | -2.06 | 0.070 |
Both of the remaining predictors — \(x_{2} \) and \(x_{3} \) — are candidates to be entered into the stepwise model because each t-test P-value is less than \(\alpha_E = 0.15\). The predictor \(x_{2} \) has the smallest t-test P-value (0.052). Therefore, as a result of the third step, we enter \(x_{2} \) into our stepwise model.
Now, since \(x_{1} \) and \(x_{4} \) were the first predictors in the model, we must step back and see if entering \(x_{2} \) into the stepwise model affected the significance of the \(x_{1} \) and \(x_{4} \) predictors. Indeed, it did — the t-test P-value for testing \(\beta_{4} \) = 0 is 0.205, which is greater than \(α_{R} = 0.15\). Therefore, we remove the predictor \(x_{4} \) from the stepwise model, leaving us with the predictors \(x_{1} \) and \(x_{2} \) in our stepwise model:
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 52.577 | 2.286 | 23.00 | 0.000 |
x1 | 1.4683 | 0.1213 | 12.10 | 0.000 |
x2 | 0.66225 | 0.04585 | 14.44 | 0.000 |
Now, we proceed to fit each of the three-predictor models that include \(x_{1} \) and \(x_{2} \) as predictors — that is, we regress \(y\) on \(x_{1} \), \(x_{2} \), and \(x_{3} \); and we regress \(y\) on \(x_{1} \), \(x_{2} \), and \(x_{4} \), obtaining:
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 71.65 | 14.14 | 5.07 | 0.001 |
x1 | 1.4519 | 0.1170 | 12.41 | 0.000 |
x2 | 0.4161 | 0.1856 | 2.24 | 0.052 |
x4 | -0.2365 | 0.1733 | -1.37 | 0.205 |
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 48.194 | 3.913 | 12.32 | 0.000 |
x1 | 1.6959 | 0.2046 | 8.29 | 0.000 |
x2 | 0.65691 | 0.04423 | 14.85 | 0.000 |
x3 | 0.2500 | 0.1847 | 1.35 | 0.209 |
Neither of the remaining predictors — \(x_{3} \) and \(x_{4} \) — are eligible for entry into our stepwise model, because each t-test P-value — 0.209 and 0.205, respectively — is greater than \(\alpha_{E} \) = 0.15. That is, we stop our stepwise regression procedure. Our final regression model, based on the stepwise procedure contains only the predictors \(x_1 \text{ and } x_2 \colon \)
Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
Constant | 52.577 | 2.286 | 23.00 | 0.000 |
x1 | 1.4683 | 0.1213 | 12.10 | 0.000 |
x2 | 0.66225 | 0.04585 | 14.44 | 0.000 |
Whew! That took a lot of work! The good news is that most statistical software — including Minitab — provides a stepwise regression procedure that does all of the dirty work for us. For example in Minitab, select Stat > Regression > Regression > Fit Regression Model, click the Stepwise button in the resulting Regression Dialog, select Stepwise for Method, and select Include details for each step under Display the table of model selection details. Here's what the Minitab stepwise regression output looks like for our cement data example:
Stepwise Selection of Terms
Candidate terms: x1, x2, x3, x4
Terms | -----Step 1----- | -----Step 2----- | -----Step 3----- | -----Step 4----- | ||||
|---|---|---|---|---|---|---|---|---|
Coef | P | Coef | P | Coef | P | Coef | P | |
Constant | 117.57 | 103.10 | 71.6 | 52.58 | ||||
x4 | -0.738 | 0.001 | -0.6140 | 0.000 | -0.237 | 0.205 | ||
x1 | 1.440 | 0.000 | 1.452 | 0.000 | 1.468 | 0.000 | ||
x2 | 0.416 | 0.052 | 0.6623 | 0.000 | ||||
S | 8.96390 | 2.73427 | 2.30874 | 2.40634 | ||||
R-sq | 67.45% | 97.25% | 98.23% | 97.44% | ||||
R-sq(adj) | 64.50% | 96.70% | 97.64% | 97.44% | ||||
R-sq(pred) | 56.03% | 95.54% | 96.86% | 96.54% | ||||
Mallows' Cp | 138.73 | 5.50 | 3.02 | 2.68 | ||||
\(\alpha\) to enter =0.15, \(\alpha\) to remove 0.15
Minitab tells us that :
- a stepwise regression procedure was conducted on the response \(y\) and four predictors \(x_{1} \) , \(x_{2} \) , \(x_{3} \) , and \(x_{4} \)
- the Alpha-to-Enter significance level was set at \(\alpha_E = 0.15\) and the Alpha-to-Remove significance level was set at \(\alpha_{R} = 0.15\)
The remaining portion of the output contains the results of the various steps of Minitab's stepwise regression procedure. One thing to keep in mind is that Minitab numbers the steps a little differently than described above. Minitab considers a step any addition or removal of a predictor from the stepwise model, whereas our steps — step #3, for example — consider the addition of one predictor and the removal of another as one step.
The results of each of Minitab's steps are reported in a column labeled by the step number. It took Minitab 4 steps before the procedure was stopped. Here's what the output tells us:
- Just as our work above showed, as a result of Minitab's first step, the predictor \(x_{4} \) is entered into the stepwise model. Minitab tells us that the estimated intercept ("Constant") \(b_{0} \) = 117.57 and the estimated slope \(b_{4} = -0.738\). The P-value for testing \(\beta_{4} \) = 0 is 0.001. The estimate S, which equals the square root of MSE, is 8.96. The \(R^{2} \text{-value}\) is 67.45% and the adjusted \(R^{2} \text{-value}\) is 64.50%. Mallows' Cp-statistic, which we learn about in the next section, is 138.73. The output also includes a predicted \(R^{2} \text{-value}\), which we'll come back to in Section 10.5.
- As a result of Minitab's second step, the predictor \(x_{1} \) is entered into the stepwise model already containing the predictor \(x_{4} \). Minitab tells us that the estimated intercept \(b_{0} = 103.10\), the estimated slope \(b_{4} = -0.614\), and the estimated slope \(b_{1} = 1.44\). The P-value for testing \(\beta_{4} = 0\) is < 0.001. The P-value for testing \(\beta_{1} = 0\) is < 0.001. The estimate S is 2.73. The \(R^{2} \text{-value}\) is 97.25% and the adjusted \(R^{2} \text{-value}\) is 96.70%. Mallows' Cp-statistic is 5.5.
- As a result of Minitab's third step, the predictor \(x_{2} \) is entered into the stepwise model already containing the predictors \(x_{1} \) and \(x_{4} \). Minitab tells us that the estimated intercept \(b_{0} = 71.6\), the estimated slope \(b_{4} \) = -0.237, the estimated slope \(b_{1} = 1.452\), and the estimated slope \(b_{2} = 0.416\). The P-value for testing \(\beta_{4} = 0\) is 0.205. The P-value for testing \(\beta_{1} = 0\) is < 0.001. The P-value for testing \(\beta_{2} = 0\) is 0.052. The estimate S is 2.31. The \(R^{2} \text{-value}\) is 98.23% and the adjusted \(R^{2} \text{-value}\) is 97.64%. Mallows' Cp-statistic is 3.02.
- As a result of Minitab's fourth and final step, the predictor \(x_{4} \) is removed from the stepwise model containing the predictors \(x_{1} \), \(x_{2} \), and \(x_{4} \), leaving us with the final model containing only the predictors \(x_{1} \) and \(x_{2} \). Minitab tells us that the estimated intercept \(b_{0} = 52.58\), the estimated slope \(b_{1} = 1.468\), and the estimated slope \(b_{2} = 0.6623\). The P-value for testing \(\beta_{1} = 0\) is < 0.001. The P-value for testing \(\beta_{2} \) = 0 is < 0.001. The estimate S is 2.41. The \(R^{2} \text{-value}\) is 97.87% and the adjusted \(R^{2} \text{-value}\) is 97.44%. Mallows' Cp-statistic is 2.68.
Does the stepwise regression procedure lead us to the "best" model? No, not at all! Nothing occurs in the stepwise regression procedure to guarantee that we have found the optimal model. Case in point! Suppose we defined the best model to be the model with the largest adjusted \(R^{2} \text{-value}\). Then, here, we would prefer the model containing the three predictors \(x_{1} \), \(x_{2} \), and \(x_{4} \), because its adjusted \(R^{2} \text{-value}\) is 97.64%, which is higher than the adjusted \(R^{2} \text{-value}\) of 97.44% for the final stepwise model containing just the two predictors \(x_{1} \) and \(x_{2} \).
Again, nothing occurs in the stepwise regression procedure to guarantee that we have found the optimal model. This, and other cautions of the stepwise regression procedure, are delineated in the next section.
Cautions! Section
Here are some things to keep in mind concerning the stepwise regression procedure:
- The final model is not guaranteed to be optimal in any specified sense.
- The procedure yields a single final model, although there are often several equally good models.
- Stepwise regression does not take into account a researcher's knowledge about the predictors. It may be necessary to force the procedure to include important predictors.
- One should not over-interpret the order in which predictors are entered into the model.
- One should not jump to the conclusion that all the important predictor variables for predicting \(y\) have been identified, or that all the unimportant predictor variables have been eliminated. It is, of course, possible that we may have committed a Type I or Type II error along the way.
- Many t-tests for testing \(\beta_{k} = 0\) are conducted in a stepwise regression procedure. The probability is therefore high that we included some unimportant predictors or excluded some important predictors.
It's for all of these reasons that one should be careful not to overuse or overstate the results of any stepwise regression procedure.
Example 10-2: Blood Pressure Section
Some researchers observed the following data (Blood pressure dataset) on 20 individuals with high blood pressure:
- blood pressure (\(y = BP \), in mm Hg)
- age (\(x_{1} = \text{Age} \), in years)
- weight (\(x_{2} = \text{Weight} \), in kg)
- body surface area (\(x_{3} = \text{BSA} \), in sq m)
- duration of hypertension ( \(x_{4} = \text{Dur} \), in years)
- basal pulse (\(x_{5} = \text{Pulse} \), in beats per minute)
- stress index (\(x_{6} = \text{Stress} \) )
The researchers were interested in determining if a relationship exists between blood pressure and age, weight, body surface area, duration, pulse rate, and/or stress level.
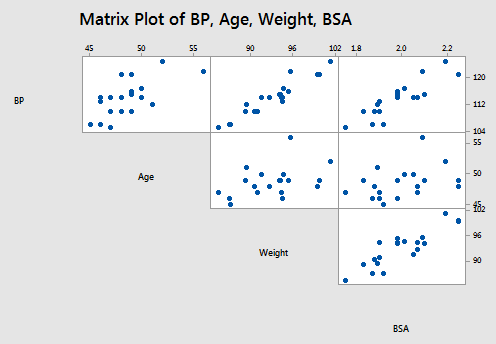
The matrix plot of BP, Age, Weight, and BSA looks like this:
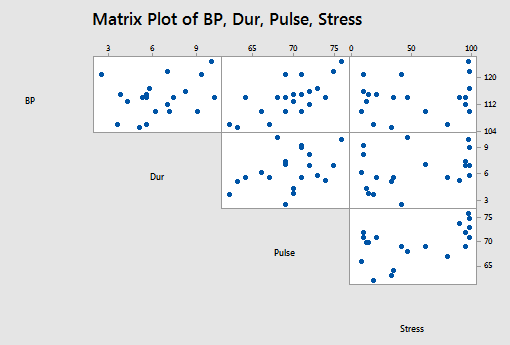
and the matrix plot of BP, Dur, Pulse, and Stress looks like this:
Using Minitab to perform the stepwise regression procedure, we obtain:
Stepwise Selection of Terms
Candidate terms: Age, Weight, BSA, Pulse, Stress
Terms | -----Step 1----- | -----Step 2----- | -----Step 3----- | |||
|---|---|---|---|---|---|---|
Coef | P | Coef | P | Coef | P | |
Constant | 2.21 | -16.58 | -13.67 | |||
Weight | 1.2009 | 0.000 | 1.0330 | 0.000 | 0.9058 | 0.000 |
Age | 0.7083 | 0.000 | 0.7016 | 0.008 | ||
BSA | 4.63 | 0.008 | ||||
S | 1.74050 | 0.532692 | 0.437046 | |||
R-sq | 90.26% | 99.14% | 99.45% | |||
R-sq(adj) | 89.72% | 99.04% | 99.35% | |||
R-sq(pred) | 88.53% | 98.89% | 99.22% | |||
Mallows' Cp | 312.81 | 15.09 | 6.43 | |||
\(\alpha\) to enter =0.15, \(\alpha\) to remove 0.15
When \( \alpha_{E} = \alpha_{R} = 0.15\), the final stepwise regression model contains the predictors of Weight, Age, and BSA.
The following video will walk through this example in Minitab.
Try it!
Stepwise regression Section
Brain size and body size. Imagine that you do not have automated stepwise regression software at your disposal, and conduct the stepwise regression procedure on the IQ size data set. Setting Alpha-to-Remove and Alpha-to-Enter at 0.15, verify the final model obtained above by Minitab.
That is:
- First, fit each of the three possible simple linear regression models. That is, regress PIQ on Brain, regress PIQ on Height, and regress PIQ on Weight. (See Minitab Help: Performing a basic regression analysis). The first predictor that should be entered into the stepwise model is the predictor with the smallest P-value (or equivalently the largest t-statistic in absolute value) for testing \(\beta_{k} = 0\), providing the P-value is smaller than 0.15. What is the first predictor that should be entered into the stepwise model?
a. Fit individual models.
PIQ vs Brain, PIQ vs Height, and PIG vs Weight.
b. Include the predictor with the smallest p-value < \(\alpha_E = 0.15\) and largest |T| value.
Include Brain as the first predictor since its p-value = 0.019 is the smallest.
Term
Coef
SE Coef
T-Value
P-Value
Constant
4.7
43.7
0.11
0.916
Brain
1.177
0.481
2.45
0.019
Term
Coef
SE Coef
T-Value
P-Value
Constant
147.4
64.3
2.29
0.028
Height
-0.527
0.939
-0.56
0.578
Term
Coef
SE Coef
T-Value
P-Value
Constant
111.0
24.5
4.53
0.000
Weight
0.002
0.160
0.02
0.988
- Now, fit each of the possible two-predictor multiple linear regression models which include the first predictor identified above and each of the remaining two predictors. (See Minitab Help: Performing a basic regression analysis). Which predictor should be entered into the model next?
a. Fit two predictor models by adding each remaining predictor one at a time.
Fit PIQ vs Brain, Height, and PIQ vs Brain, Weight.
b. Add to the model the 2nd predictor with smallest p-value < \(\alpha_E = 0.15\) and largest |T| value.
Add Height since its p-value = 0.009 is the smallest.
c. Omit any previously added predictors if their p-value exceeded \(\alpha_R = 0.15\)
The previously added predictor Brain is retained since its p-value is still below \(\alpha_R\).
FINAL RESULT of step 2: The model includes the two predictors Brain and Height.
Term
Coef
SE Coef
T-Value
P-Value
Constant
111.3
55.9
1.99
0.054
Brain
2.061
0.547
3.77
0.001
Height
-2.730
0.993
-2.75
0.009
Term
Coef
SE Coef
T-Value
P-Value
Constant
4.8
43.0
0.11
0.913
Brain
1.592
0.551
2.89
0.007
Weight
-0.250
0.170
-1.47
0.151
Term
Coef
SE Coef
T-Value
P-Value
Constant
111.0
24.5
4.53
0.000
Weight
0.002
0.160
0.02
0.988
- Continue the stepwise regression procedure until you can not justify entering or removing any more predictors. What is the final model identified by your stepwise regression procedure?
Fit three predictor models by adding each remaining predictor one at a time.
Run PIQ vs Brain, Height, Weight - weight is the only 3rd predictor.
Add to the model the 3rd predictor with the smallest p-value < \( \alpha_E\) and largest |T| value.
Do not add weight since its p-value \(p = 0.998 > \alpha_E = 0.15\)
Term
Coef
SE Coef
T-Value
P-Value
Constant
111.4
63.0
1.77
0.086
Brain
2.060
0.563
3.66
0.001
Height
-2.73
1.23
-2.22
0.033
Weight
0.001
0.197
0.00
0.998
Omit any previously added predictors if their p-value exceeded \(\alpha_R\).
The previously added predictors Brain and Height are retained since their p-values are both still below \(\alpha_R\).
Term
Coef
SE Coef
T-Value
P-Value
Constant
111.3
55.9
1.99
0.054
Brain
2.061
0.547
3.77
0.001
Height
-2.730
0.993
-2.75
0.009
The final model contains the two predictors, Brain and Height.